细线绕柱问题的探讨

李 力

（重庆清华中学 重庆 400054）

在普通物理的力学课程里，细线绕柱问题比较常见，“如图1，在光滑水平面上立一圆柱，在其上缠绕一根细线，线的另一头系一个质点.起初将一段线拉直，横向给质点一个冲击力，使它开始绕柱旋转.在此后的时间里线愈绕愈短，质点的角速度怎样变化？其角动量守恒吗？动能守恒吗？”［1］

图1

图2

笔者认为上述解答中，“质点的角动量减少”是对的，“角速度增大”也是正确的（此点说理不够充分），但“绳的张力做了功”和“动能增加”则不对.事实上，绳不断地缠绕在光滑圆柱的过程中，质点速度与细绳总是垂直的，从而绳的张力不做功，质点的动能守恒，下面我们详加分析.

把质点在运动中细绳缠绕圆周的过程“回放”，不难意识到质点的运动轨迹正是圆周的渐开线.数学上一般的平面封闭凸曲线C的渐开线是这样定义的［2］：把绕在一个平面封闭凸曲线C上的不可伸长的细绳伸开，保持细绳与曲线C在将要离开的点相切，这时绳端画出的运动轨迹L叫所绕曲线C的渐开线.

渐开线有一条重要性质［2］即渐开线L在任一点的法线与所绕曲线C相切.而细绳与凸曲线C处处相切，所以，质点运动轨迹的法线与细绳是重合的，这正是质点速度（在运动轨迹的切线方向上）与细绳垂直的原因.

由于前述问题中细线绕的是圆柱，所以，我们来证明圆的渐开线具有这条性质.如图3，设定圆的中心为O，半径为R，而A是绳子未拉开时绳端质点的位置.现取O为原点，过O与A的直线为x轴.设M（x，y）是圆的渐开线上任意一点，这时绳子的一段为直线MT，且是圆的切线.令 ∠AOT＝θ，则渐开线的方程为［2］

图3

x＝R（cosθ＋θsinθ）

y＝R（sinθ－θcosθ）

与M对应的圆周上的动点T的坐标为xT＝Rcosθ，yT＝Rsinθ，所以，动点T和M的速度分别为

易证：vT·v＝0，即vT与v互相垂直，这说明渐开线上M点的切线与圆周上相应点T的切线彼此垂直，也就是绳端质点速度与绳子MT是垂直的.

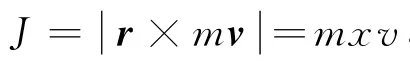
同样地，针对一般的封闭凸曲线，可以通过研究绳端质点以及绳与所绕曲线的切点的运动，简捷地证明渐开线的这条重要性质，具体的证明可参看文献［3］.

1 赵凯华，罗蔚茵.新概念物理题解（上册）.北京：高等教育出版社，2009.28

2 《数学手册》编写组.数学手册.北京：人民教育出版社，1979.379，380，400

3 李力.再谈《物块速度垂直于悬线的数学证明》.物理教师，2005.1