水下模糊图像参数估计复原方法

李一兵，付 强，张 静

（哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001）

水下图像在海洋探测中具有重要意义，通过对直观图像的研究可以获得各种未知环境的信息。由于水下复杂环境的不确定性以及各类噪声干扰的影响，水下图像处理中存在着分辨率低、边缘模糊等诸多问题，这也对进一步的判断处理带来很多困难，各种图像复原方法也一直是研究的热点［1－3］。

水下模糊图像可以视为点扩展函数（Point spread function，PSF）和原始清晰图像卷积的结果，因而复原方法主要分为两种:一种是预先知道点扩展函数的先验知识，可以直接对模糊图像进行解卷积逆运算；另一种则是点扩展函数未知，即不具备图像先验知识的条件下，通过参数估计的方法实现图像的盲复原。实际情况中退化图像的点扩展函数参数难以获取，只能在有限的先验知识条件下估计原始图像，即图像盲复原，文献［4］提出了一种基于K－L信息的图像盲复原方法。解卷积（逆滤波）是被广泛采用的具有代表性的方法，文献［5］提出了一种结合时域空域特性去除运动模糊的逆滤波方法，其他方法包括全变分法［6］、最大熵法、ARMA参数估计法、以快速傅里叶变换为基础的迭代盲反卷积算法（IBD）、模拟退火法等，但这些方法存在着收敛性不好、计算量大［7－8］等问题。针对上述问题，拉东变换可以计算图像投影，对于平移运动中的角度和位移检测有较好的效果［9］，可以应用于图像模糊参数估计和复原。

本文首先介绍图像的退化模型，分析常见的模糊类型以及解卷积的复原方法，然后针对不同的运动模糊类型采用适宜的参数估计解卷积方法完成图像复原。

1 图像模糊退化

1.1 图像退化模型

在加性噪声n （x，y）的影响下，输入原始图像f （x，y），经过退化算子H （x，y）后产生的退化图像g （x，y）可以表示为［10－11］:

通常原始图像f（x，y）可以表示为

后续介绍的模糊模型均具有上述表示，所作的研究也是对线性图像恢复的研究。

1.2 模糊退化模型

常见的模糊退化模型有运动模糊（机械性模糊）、高斯模糊和离焦模糊（光学性模糊）。运动模糊主要是由于成像系统与目标的相对运动，导致成像在某个方向上形成模糊。任意方向的运动模糊可以视为在该方向上的水平运动。以偏移旋转角度α和移动像素数d为例，点扩展函数可以表示为

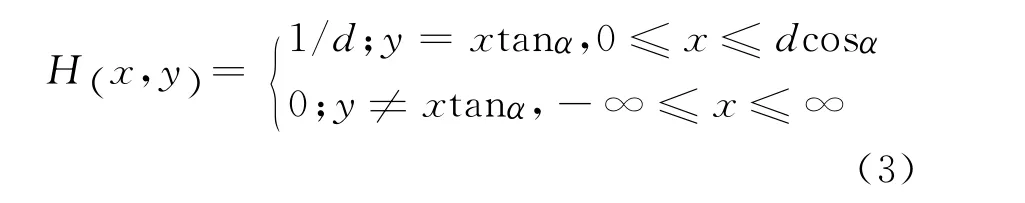
高斯模糊可以认为是人为引入的模糊，点扩展函数可以表示为

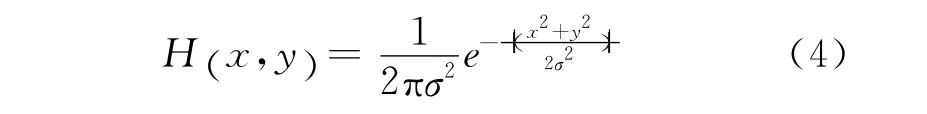
式中:σ为高斯模糊的标准差。

离焦模糊主要是由成像时偏离正确聚焦点而造成的，点扩展函数为

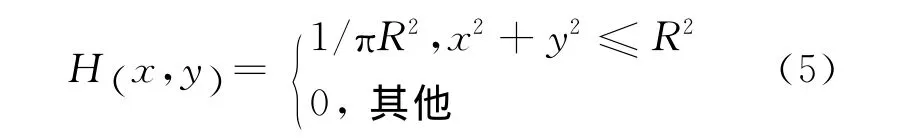
式中:R为模糊半径。

若能预先识别出图像的模糊类型，则可以对PSF形式做出较为准确的估计，提高复原的精度。但对于获取的模糊图像而言，单从直观的视觉效果上未必能很准确地判断出造成模糊的原因所在，所以鉴别模糊图像的类型是十分必要的。文献［12－13］提出了利用神经网络进行模糊类型判断的方法，这种方法判断的准确性较高，但对于前期的学习训练要求也较高，复杂度较大。鉴于一幅图像因不同模糊类型会导致频谱中不同频率成分的丢失，在频域上呈现出不同性质，故依据不同的频谱特点可以鉴别图像的模糊类型。在实际处理中，通过对模糊图像加以频谱分析可以区分出模糊类型。该方法简单易行，无需复杂计算，也适于进一步采取不同的处理方法。如图1所示，第一行从左至右分别显示不同退化模糊的图像，第二行依次显示各图像对应的二维傅里叶变换，从频谱的特征差异可以显著区分出不同的模糊类型:运动模糊的频谱呈现出平行栅状，高斯模糊频谱呈现为网格棋盘状，而离焦模糊的频谱则呈现同心圆环状。

图1 不同模糊效果对比Fig.1 Comparison of different blur effect

1.3 图像反卷积算法

通过前面的图像退化模型的推导可知，利用反卷积可以实现图像的复原，其核心是点扩散函数PSF的确定。常用的反卷积复原方法有维纳滤波、最小二乘滤波和L－R算法。

维纳滤波尝试寻找一个使统计误差函数最小的估计，但系统被假设为线性的，而实际图像的记录和评价图像的人类视觉系统往往都是非线性的。且基于最小均方误差的准则与人类视觉判决准则并不吻合，实际得到的结果只能是平均意义上的最优解。最为关键的是:维纳滤波需要了解真实图像以及噪声的大量先验知识，这在实际中是不可获得的。

约束最小二乘方（正则）滤波的提出可在一定程度上解决上述问题:正则滤波只需要噪声的方差均值，且对所处理的每幅图像均可达到最有效果。

Lucy－Richardson（L－R）算法来源于最大似然公式，在该方法中图像用泊松统计加以模型化，实际中采取迭代收敛的办法得到模型的最大似然函数。

由以上的分析可知:图像复原的难易程度主要取决于对退化过程的先验知识掌握的精确程度。若对退化的类型、机制十分清楚，那么就可以根据图像退化的先验知识建立退化模型，采用各种反卷积处理方法对图像进行复原处理。然而，实际图像处理时，许多先验知识（包括图像及成像系统）往往并不具备。某些情况下，要得到图像的先验知识需要付出很大的代价，甚至有些是不可实现的。针对基于点扩散函数的参数难以把握和预知，提出了图像盲复原技术这一课题。实际情况下，必须在没有退化先验知识或者只有少量先验知识的情况下，从模糊图像中估计真实图像和退化函数，这种方法就是图像盲复原。针对以上分析的不同模糊模型和反卷积复原方法，实验结果表明对于运动模糊和高斯模糊，维纳滤波和正则滤波的效果较好，而L－R算法则更适合于高斯模糊和离焦模糊。

2 点扩展函数的参数估计

2.1 复原运动模糊

Radon变换是计算图像在某一指定角度射线方向上投影的变换方法。二维函数f （x，y）的投影就是其在指定方向上的线积分，即f （x，y）的Radon变换为:

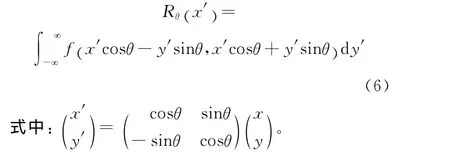
所得线积分的结果为沿条纹方向的投影变换，在中心位置的积分值最大，运动模糊可以看作原始图像像素沿模糊角度的方向上产生了大小等于模糊长度的位移，因而利用Radon变换可以较准确地检测运动模糊［14］。在估计模糊角度时首先计算模糊图像的二维傅里叶变换，为了增强条纹效果，对变换后的频谱进行取模和对数运算，再利用循环移位使低频成分位于频谱中心，利用Radon变换得到投影，投影值中最大值所对应的列即为模糊的角度。具体步骤如下:

（1）对模糊图像做二维傅立叶变换，即B＝fft2（Blurred）。

（2）增强频谱的条纹效果，C＝lg（1＋abs（B））。

（3）将低频成分移位至频谱中心，D＝fftshift（C）。

（4）对频谱进行拉东变换［R，xp］＝radon（D，θ）。

（5）求取投影最大值对应的角度（即为模糊角度b＝max（R））。

仿真实验中模糊角度的范围为0°～180°，如图2中实线所示，估计角度如虚线所示。可以看出估计角度与真实角度十分接近，实测结果最大偏差为3°。

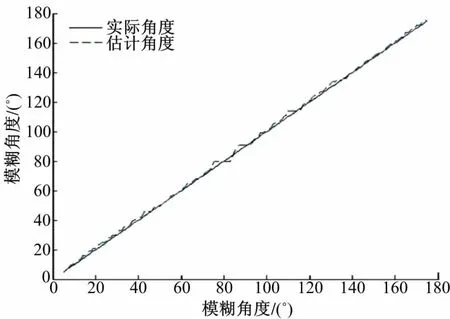
图2 模糊角度的估计Fig.2 Estimation of motion angle

在运动模糊中，模糊尺度参数是指原始图像中点目标在运动模糊后形成模糊带的宽度。常用的确定模糊尺度的方法有模糊图像的二维频谱沿着运动模糊方向作Radon变换投影，利用退化算子求取微分及自相关函数，并搜索各列取和后最小和所在的列［15］。

该方法存在的问题是计算复杂，极小值点的确定不易精确求得，而且在有噪声干扰的情况下检测效果会受到较大影响。基于以上考虑本文做出的改进检测方法如下:

（1）求退化图像g离散傅立叶变换如下:

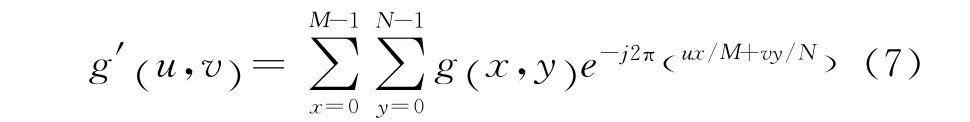
可以利用快速傅立叶变换近似得到。

（3）对于s取对数后各列求和，得到一个行矩阵S。

（4）绘制出S的曲线，依据尖峰个数判断出模糊尺度。

通过仿真实验对模糊图像进行长度估计，分别以模糊长度7、10、15、20进行测试，从变换后的求和曲线（见图3）尖峰的个数N（分别为7、10、15、20）可以准确得到模糊长度L，二者具有一一对应的关系。实验结果表明，本方法对于模糊长度可以做到检测准确度高、且计算复杂度低。

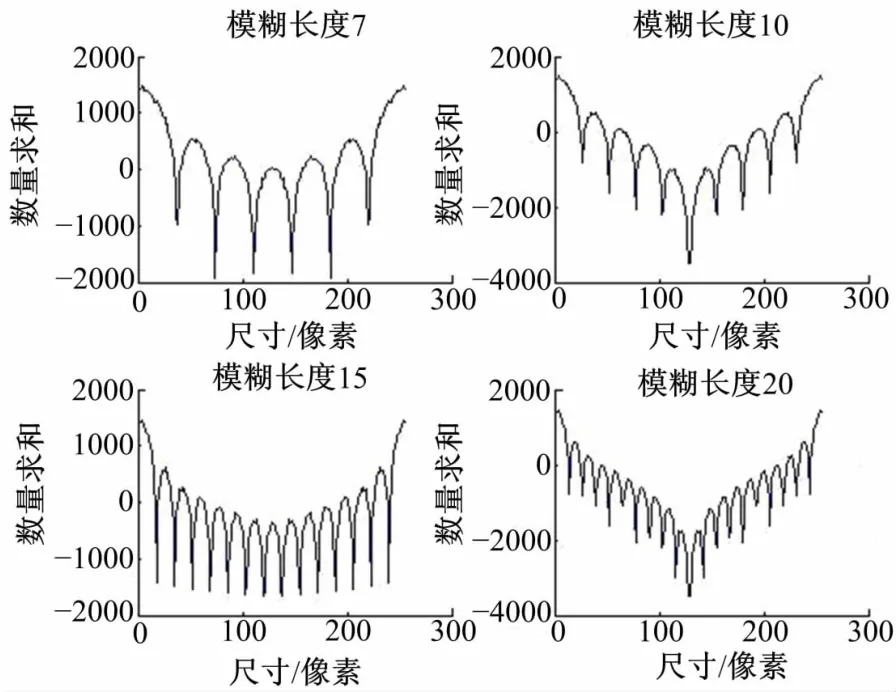
图3 模糊长度的估计Fig.3 Estimation of motion length

2.2 复原高斯模糊

高斯模糊的点扩展函数关键在于模糊方差的估计。常用的估计方法有如下几种［16－18］:

（1）多尺度小波变换参数估计，对图像进行不同尺度小波变换，分别计算小波模极大值，并依据李氏级数得到高斯模糊方差。

（2）图像多项式变换的边缘检测。

（3）基于局部方差的边缘检测模糊估计。

2.3 复原离焦模糊

离焦模糊图像复原中常把点扩散函数近似为圆柱形函数，因而若能有效估计圆柱形的半径，则等价于求出了离焦模糊点扩散函数。以往复原的方法有:基于倒谱分析的离焦模糊识别，但对于较大和较小的模糊半径效果不好。基于小波的盲复原计算量大且受噪声影响大。利用Hough变换检测频谱图像半径后采用拉格朗日内插曲线拟合的方法计算复杂度高，参数估计不够准确。利用八领域拉普拉斯算子对离焦图像进行无方向性的二阶微分，然后求取微分图像的自相关，通过三维显示观察环形槽的位置，槽底位置连成鉴别圆。该鉴别圆的直径等于离焦点扩散函数圆柱直径的两倍。

3 基于参数估计和模糊分类的复原方法

需要指出的是，由于水下噪声的影响即使点扩散函数已知，反卷积问题由于其自身的病态性（ill－posed）也不是一个简单的问题。此时的图像退化方程为第一类Fredholm方程，其求解是一个不适定问题，表现为方程的解不连续、依赖于观测数据，即图像中的噪声影响以及观测数据的微小变动都可能导致方程最终求解的极大变动，而且会造成复原算法计算量大，结果质量难以保证，因此对于水下图像中噪声的预处理就显得更有实际意义。图像的噪声主要来源于图像的获取和传输过程，水下环境中的光照和污染是噪声产生的最主要原因，在处理时一般将其看作脉冲椒盐噪声和高斯噪声的混合。

鉴于噪声对于后续的参数估计及反卷积复原有着较大影响，因而对于图像去噪预处理就显得非常重要。本文采取中值滤波和小波阈值去噪的方法去除混杂在图像中的椒盐和高斯噪声，将噪声的影响降到最低。

如图4的流程图所示，首先对含有噪声的模糊图像进行去噪预处理，然后利用傅立叶变换获得图像的频谱信息，依据不同的频谱特征确定图像的模糊类型，然后应用不同的退化模型做出相应的估计复原。对于运动模糊，重点是估计偏移的模糊角度和移动的模糊长度；对于高斯模糊和离焦模糊则分别估计噪声方差和离焦半径。得到参数的估计值后，采取合适的反卷积方法进行解卷积，可以得到最终的复原图像。

图4 图像去噪分类复原流程图Fig.4 Flow chart of image restoration method

具体实施步骤为:

（1）获取原始含噪声模糊图像，利用中值滤波和小波阈值去噪对图像进行预处理。

（2）求得图像的傅立叶频谱，对图像的模糊类型做出判断。

（3）对于不同的模糊类型采取不同参数估计方法，得到点扩展函数的参数估计。

（4）采取合适的解卷积方法完成图像复原。

4 实验结果与分析

为了检验复原方法效果，对比实验以256×256像素的水下图像在三种运动模糊情况下进行复原，三种情况分别是模糊角度30°，模糊长度5；模糊角度30°，模糊长度10；模糊角度45°，模糊长度10。对原始图像先去噪，然后去模糊，结果如图5～图7所示。

图5 模糊角度30°，模糊长度5Fig.5 Case of motion angle 30°with motion length 5

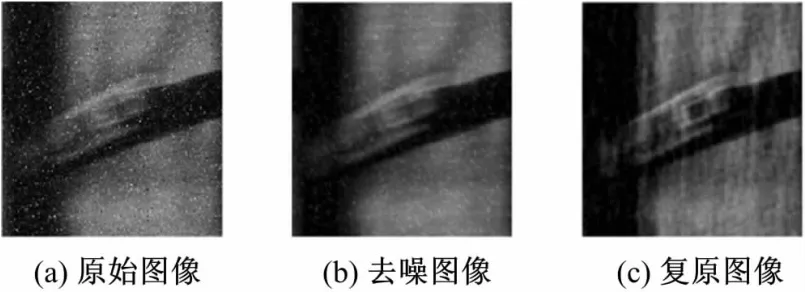
图6 模糊角度30°，模糊长度10Fig.6 Case of motion angle 30°with motion length 10

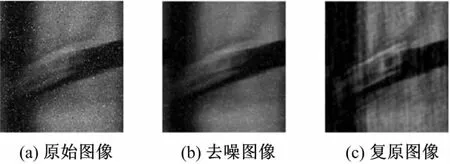
图7 模糊角度45°，模糊长度10Fig.7 Case of motion angle 45°with motion length 10

图5～图7显示的结果可以看出噪声去除对于复原的影响。采取去噪预处理的图像去除了图像中的斑点和高斯噪声，目标图像可以被较清晰地恢复出来，通过增强前后对于目标的边缘提取效果也可以看出，去除模糊提高了图像的清晰度和分辨率，如图8所示。在噪声环境下由于噪声点的干扰而无法提取目标，经去噪、去模糊后可以准确检测到目标边缘。

图8 利用Sobel算子进行边缘检测Fig.8 Edge detection by Sobel operator

从表1所示图像在不同模糊条件下增强后峰值信噪比（PSNR）的结果可以看出:经过去噪处理后的增强结果相比于原始模糊图像能提高5 dB的峰值信噪比。

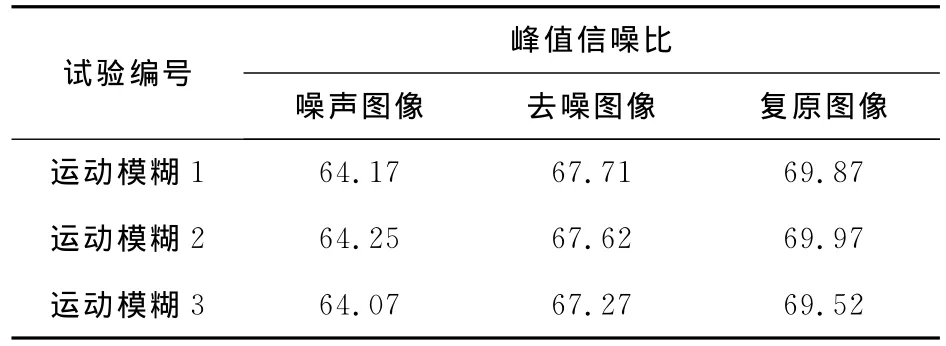
表1 不同模糊下增强图像峰值信噪比（PSNR）（单位:dB）Table 1 Comparison of PSNR among enhanced images

5 结束语

论述了对不同模糊类型的水下图像的复原方法。首先对模糊图像进行去噪预处理，通过对傅立叶频谱的分析判定模糊类型，通过不同的参数估计得到复原所需的信息，然后采用合适的反卷积方法得到最终的复原图像。相比于其他图像复原算法，在运动模糊的估计上提出了基于拉东变换改进方法，在降低复杂度的同时提高了准确度，同时进行了去噪预处理以及模糊类型的区分，在复原中取得了较好的效果。在成像条件复杂、环境恶劣、图像质量低等场合具有实际应用的潜力。但本文讨论的情况只限于单一模糊情况，对于混合模糊噪声模型的研究将是下一步的重点。

［1］Raimondo Schettini，Silvia Corchs.Underwater image processing:state of art of restoration and image enhancement methods［C］∥EURASIP Journal on Advances in Signal Processing，2010:1－14.

［2］朱殿尧，卞红雨.侧扫声纳目标自动探测研究［J］.吉林大学学报:信息科学版，2008，26（6）:627－631.Zhu Dian－yao，Bian Hong－yu.Image research of sidescan sonar target auto detection［J］.Journal of Jilin University（Information Science Edition），2008，26（6）:627－631.

［3］赵春晖，李誉斐.基于改进直方图不变矩的声呐图像识别方法［J］.应用科技，2007，34（11）:19－24.Zhao Chun－hui，Li Yu－fei.Recognition for sonar image based on improved histogram invariant moments［J］.Applied Science and Technology，2007，34（11）:19－24.

［4］Abd－Krim Segouane.A Kullback－Leibler divergence approach to blind image restoration［J］.IEEE Transaction on Image Processing，2011，20（7）:2078－2083.

［5］Hiloyuki Takeda，Peyman Milanfar.Removing motion blur with space－ime processing ［J］.IEEE Transaction on Image Processing，2011，20（10）:2990－3000.

［6］Michailovich Oleg V.An iterative shrinkage approach to total－variation image restoration［J］.IEEE Transaction on Image Processing，2011，20（5）:1281－1299.

［7］Deepa Kundur，Dimitrios Hatzinakos.Blind image deconvolution［J］.IEEE Signal Processing Magazine，1996（5）:43－64.

［8］Anat Levin，Yair Weiss，Fredo Durand，et al.Understanding blind deconvolution algorithms［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（12）:2354－2367.

［9］Peyman Milanfar.A model of the effect of image motion in the Radon transform domain［J］.IEEE Transactions on Image Processing，1999，8（9）:1276－1281.

［10］Liu Xian－ming，Zhao De－bin，Xiong Rui－qin.Image interpolation via regularized local linear regression［J］.IEEE Transactions on Image Processing，2011，20（12）:3455－3469.

［11］Gonzales Rafael C，Woods Richard E.数字图像处理［M］.（3版）阮秋琦，阮宇智译.北京:电子工业出版社，2011:218－224.

［12］尹兵，王延斌，刘威.用神经网络鉴别退化图像的模糊类型［J］.光学技术，2006，32（1）:138－140.Yin Bing，Wang Yan－bin，Liu Wei.Blur identification of the degraded images by neural network［J］.Optical Technique，2006，32（1）:138－140.

［13］Li Da－long，Mersereau Russell M，Simske Steven.Blind image deconvolution through support vector regression［J］.IEEE Transactions on Neutral Networks，2007，18（3）:931－935.

［14］王婷.退化图像的复原改进算法研究与实现［D］.哈尔滨:哈尔滨工程大学，2007.Wang Ting.The study and realization about the improved restoration algorithm of degraded image［D］.Harbin:University of Harbin Engineering，2007.

［15］彭青建.运动模糊图像复原算法研究［D］.西安:电子科技大学，2010.Peng Qing－jian.Motion－blur image restoration algorithm research［D］.Xi＇an:University of ESTC，2010.

［16］陶青川，邓宏彬.基于小波变换的高斯点扩展函数估计［J］.光学技术，2004，30（3）:284－288.Tao Qing－chuan，Deng Hong－bin.Wavelet transform based Gaussian point spread function estimation［J］.Optical Technique，2004，30（3）:284－288.

［17］吕成淮，何小海，陶青川，等.图像复原中高斯点扩展函数参数估计算法研究［J］.计算机工程与应用，2007，43（10）:31－34.Lyu Cheng－huai，He Xiao－hai，Tao Qing－chuan，et al.Research on estimation algorithms for Gaussian point spread function parameter in image restoration［J］.Computer Engineering and Applications，2007，43（10）:31－34.

［18］Fu Qiang，Li Yi－bing，Liu Yue.Improving image quality in poor visibility with retinex－based adaptive image eenhancement method［J］.International Journal of Digital Content Technology and Its Applications，2011，5（10）:296－301.