推挽型软开关感应耦合电能传输变换器

翟 渊，孙 跃，苏玉刚，王智慧，唐春森

（重庆大学 自动化学院，重庆 400030）

由于感应耦合电能传输（ICPT）技术是一种安全、可靠、灵活的电能接入技术而得到了广泛的应用［1－4］。在ICPT系统中直流电要由初级变换环节转换成高频交流电，为提高效率，减少开关管的损耗，一般采用软开关技术，通过增加电压过零检测电路和相应的控制电路来实现ZVS［5－6］。本文通过在传统的ICPT变换器基础上引入推挽变压器，利用变压器的输出作为逆变桥的输入，通过频率方法和增加两个电容来实现零电压的开通与关断，去掉了传统ICPT软开关变换器中存在的电压电流过零检测电路，简化了变换器的设计。开关电源中也常采用推挽电路来完成DC／DC变换，文献［7］提出了一种新型的推挽软开关谐振电路，通过在推挽变压器输出端增加补偿电容，通过电容与变压器的漏感谐振来实现零电压开通，零电流关断。由于零电流关断的条件要求较高，当负载变化时容易失去软开关特性，因此具有一定的局限性。文献［8］为提高传输效率和减小电压放大倍数，利用了两个变压器来实现推挽升压，利用两个变压器的漏感和一个额外的电容来实现软开关。由于应用领域不同，上述文献对推挽变压器和谐振网络在ICPT系统中所表现的特性都缺少相应的分析。本文对变换器软开关工作原理、软开关工作条件以及推挽变压器匝比边界条件进行了分析，可为ICPT软开关逆变器的设计提供一定的理论指导作用。

1 电路构成及软开关工作原理

1.1 推挽型软开关变换器的电路

图1所示为本文提出的推挽软开关ICPT变换器的结构图。T为推挽变压器，变压器次级接原边发射线圈Lp和原边补偿电容Cp，Lp、Cp为串联结构。副边接收线圈Ls和副边补偿电容Cs为并联结构。M为原副边线圈互感，Ls、Cs输出接整流桥，整流桥输出接滤波电容Co以及负载Ro。Cs1、Cs2为开关管Q1和Q2包括漏源极结电容在内的并联电容。

在工作过程中变压器的铁芯是双向磁化，初级线圈必须有良好的对称性，否则容易引起直流偏磁导致铁芯饱和。变压器工作在高频条件下，采用李兹线可以进一步减少损耗，提高传输效率，由于并不需要漏感来参与谐振，因此变压器应紧密缠绕从而减小漏感［9］。

1.2 软开关电路工作原理分析

推挽谐振电路的开关管两端并联了较大的电容，由于电容的电压不能突变所以电路可以实现零电压关断，为实现电路零电压开通，故使电路工作频率大于谐振回路的固有频率。由于电路工作频率高于谐振频率，故由电感和电容组成的谐振回路呈感性。下面分析推挽软开关谐振变换器的工作原理，电路工作模态如图2所示，其稳态时工作波形如图3所示。

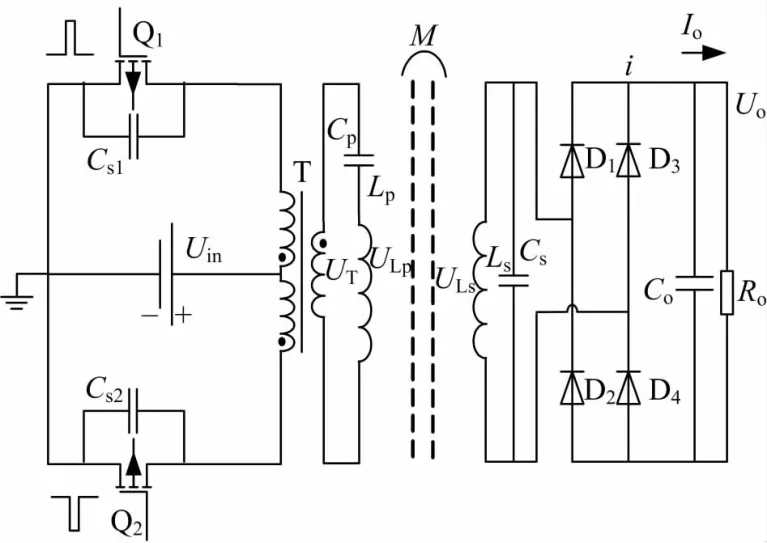
图1 推挽变换器结构框图Fig.1 Block diagram of push－pull converter

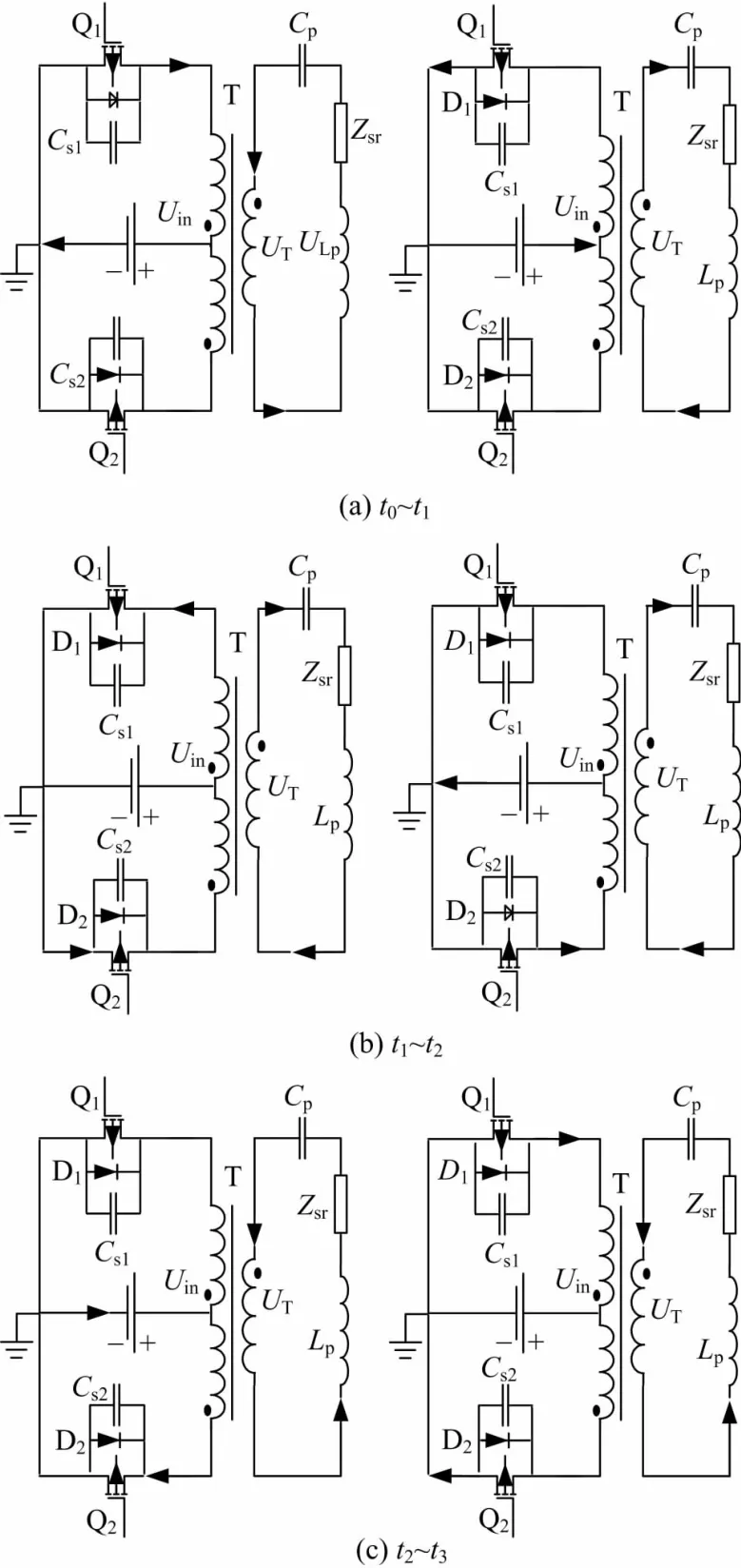
图2 变换器不同时间段工作模态Fig.2 Converter working mode at different time

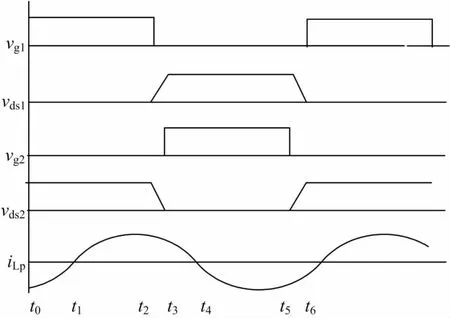
图3 变换器工作波形图Fig.3 Converter operating waveforms

在分析之前作出如下假设:

（1）所有的开关管、二极管均为理想元件，变压器为理想变压器。

（2）电感、电容均为理想元件，Cs1＝Cs2＝Cs。

（3）Zsr为副边的等效反射阻抗。

在一个开关周期中，有6种开关模态，各开关模态的工作情况描述如下:

模态1（t0～t1）:t0时刻，Q1开通，滞后的感性电流此时仍保持为负，Q1开通前一刻电流经并联的体二极管D1续流，由于体二极管D1的钳位作用，Q1两端电压近似为0，因此Q1开通时为0电压开通，Q1开通前，其并联二极管已导通，由Cp、Lp构成的谐振网络已经谐振了，流过变压器原边的电流逐渐减小，谐振电流开始准备过零，此模态持续的时间为t01。

模态2（t1～t2）:t1时刻，谐振网络电流为零，此后谐振网络开始流过正向电流，谐振网络继续谐振，此模态持续的时间为t12。

模态3（t2～t3）:t2时刻关断Q1，此时流过功率管的电流比较大，但由于功率管并联有较大的电容，由于电容两端电压不能突变会从零逐渐上升，因此Q1为零电压关断。此后Cs1开始充电，Cs2开始放电，此模态持续时间为t23。

到t3时刻，Q2开通，回路进入下半个周期（模态4、5、6），其工作过程与前面三个模态完全相同，这里不再赘述。

1.3 零电压工作条件

仅使原边谐振网络呈现感性还不能满足零电压开通的条件，还需要使开关管两端的并联电容在死区时间放电到零或充电到2Vin，在t2时刻假设谐振电流为IrL，由于死区时间远小于开关周期，因此可认为在死区时间内IrL保持不变，Cs1两端电压由0充电至2Vin，Cs2两端电压由2Vin放电到0，其中Vin为输入的直流电压。那么使功率管并联电容充放电所需的最小电流为:

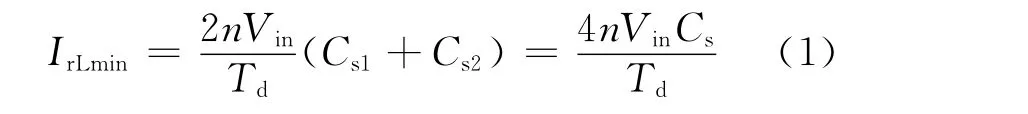
式中:n为推挽变压器次级对初级的线圈匝数比；Td为死区时间。

假设变换器的输入功率为Pin，原边谐振网络的输入电压为一频率为f0、峰值为2nVin、占空比为0.5的方波信号，此信号接谐振网络，只有基波分量会通过，则基波分量的有效值VTrms为

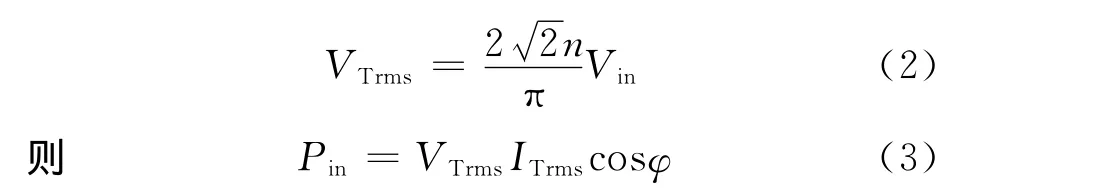
式中:ITrms为谐振网络的电流有效值；φ为电压电流的移相角。

为使开关管两端并联电容在死区时间放电到零或充电到2Vin则需:

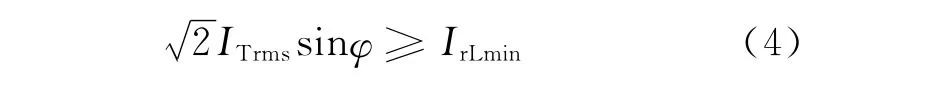
副边输入端为一并联谐振网络，根据正弦等效原理，将变换器次级整流滤波电路等效为交流负载，则其交流等效负载为

系统工作在谐振状态，忽略系统原副边线圈内阻以及器件的开关损耗，则副边等效阻抗

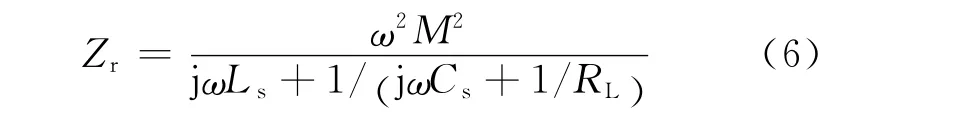
式中:ω为角频率，当系统处于谐振状态时，谐振频率及谐振角频率分别为f0及ω0，此时有ω＝ω0

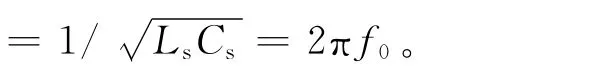
由式（6）可得谐振时副边等效阻抗，即

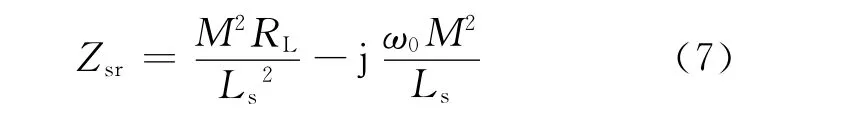
由于f0高于原边谐振网络的固有频率，因此原边谐振网络工作在感性状态，则原边谐振网络的阻抗Zn为

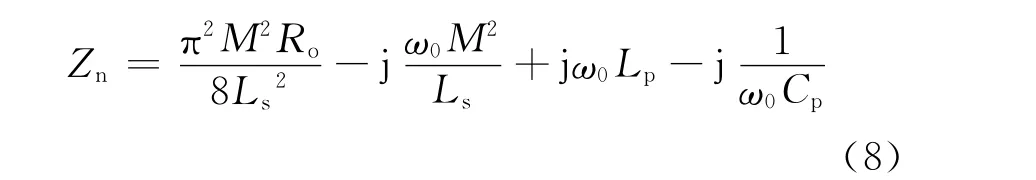
由式（1）（2）（3）（4）（5）（8）可得

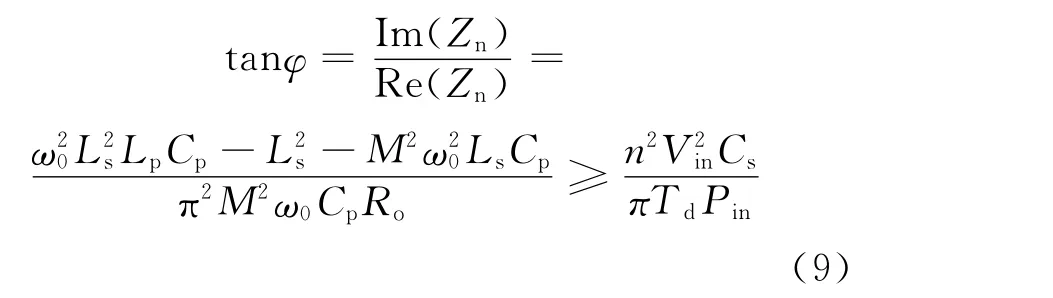
因此变换器零电压工作的条件为

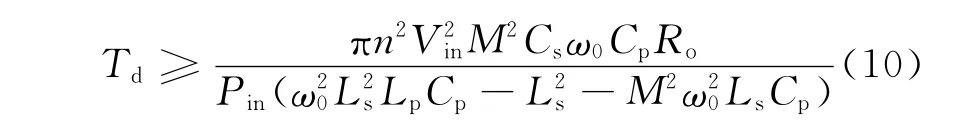
由式（10）可知，变换器工作频率固定时，若电路工作在轻载或输入电压变高时，充放电时间会变长，因此当频率固定且输入电压固定时，电路零电压导通的条件应该根据轻载条件来设定。

2 推挽变压器匝数的边界条件

电压型ICPT负载恒压控制需满足一定的前提条件［10］。当系统结构确定，则f0必须保证不变，即系统有且仅有1个谐振频率点f0。在这种条件下，变压器匝数n有一定的范围限制。

由式（2）（5）（7）可得系统输出功率Po为

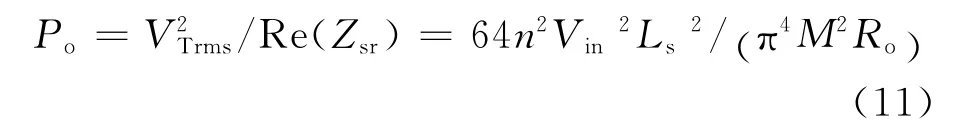
则负载两端电压Vo为

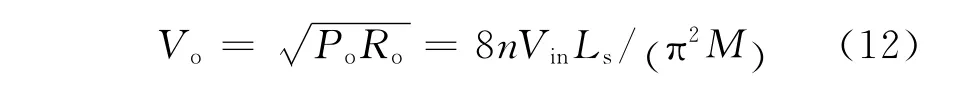
由式（12）可得变换器电压放大倍数A为

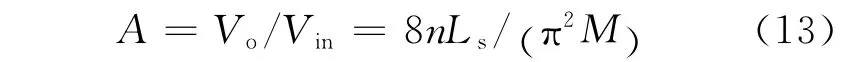
在f0、n、Ls及M等参数不变的情况下，由式（13）可知，输入电压Vin恒定时，即可保证Vo恒定，系统输出电压与负载无关。

对于SP系统副边的品质因数Qs为［11］

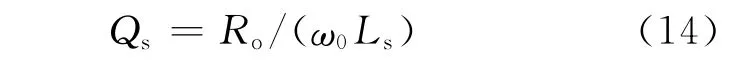
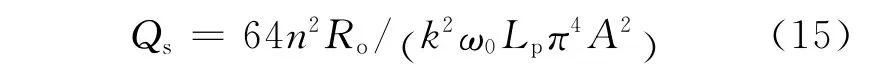
对于SP系统副边品质因数应满足［12］

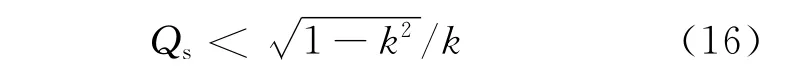
由式（14）（15）（16）可得推挽变压器次级对初级匝数比n的边界条件

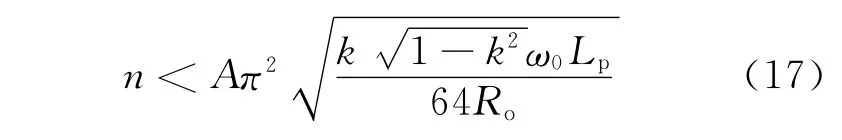
尽管通过增大推挽变压器次级对初级的匝数比可提高输出电压，但为保证系统稳定，变压器次级对初级的匝数比应满足式（17）所要求的条件，否则会出现频率分叉现象［13］。

3 仿真分析

为了验证本系统的可行性，按照图1在Saber环境中搭建了一个仿真模型，并进行了仿真分析，电路的仿真参数为:开关管采用IRFP250，开关管并联电容为0.1μF，开关管驱动频率为32.5kHz，死区时间为0.5μs，推挽变压器匝数比为3∶3∶5，原边线圈电感值为115 μH，补偿电容为0.33μF，副边线圈电感值为224 μH，谐振电容为0.1μF，原副边线圈互感因子为0.2，整流管为 MUR1560，滤波电容为100μF，负载电阻为100Ω，输入电压为DC24V。图4为变换器的仿真波形图。

图4 变换器工作仿真波形图Fig.4 Simulation waveform of converter

图4中，从上到下依次为开关管漏源极间电压波形、开关管驱动波形、原边发射线圈电流波形和负载两端电压波形，从图中可看出谐振网络的电流波形滞后于开关管两端电压波形，由于谐振网络工作在固有频率以上，因此电流波形有少许失真，由于原边工作在固有频率以上，为使副边也处于谐振状态，副边谐振网络的固有频率点应高于原边。

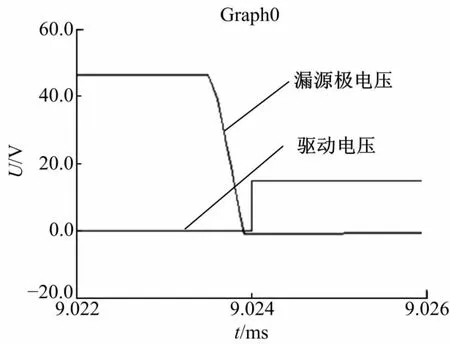
图5 开关管开通时漏源极两端电压仿真波形Fig.5 Voltage simulation waveforms of drainsource as switch turning on

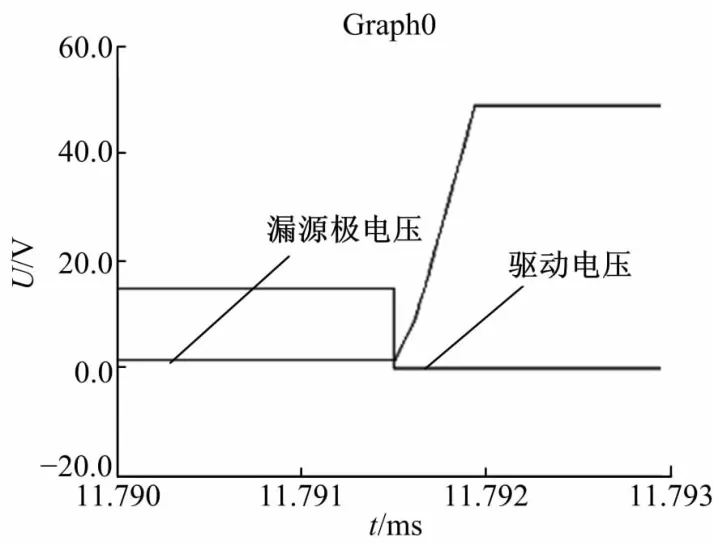
图6 开关管关断时漏源极两端电压仿真波形图Fig.6 Voltage simulation waveforms of drainsource as switch turning off

图5、图6分别为开关管Q1开通时和关断时漏源极电压和驱动电压波形仿真放大图，从图5可看出，当开关管开始工作时，其DS两端电压已经下降为零，实现了零电压开通，从图6可看出，当驱动电压变为零时，DS两端电压逐渐从零开始上升，实现了零电压关断。

4 实验验证

为了验证软开关设计的可行性，按照图1设计制作了一台基于推挽软开关的ICPT系统DCDC变换器样机。实验参数尽量按照仿真参数来设计，开关管采用IR公司的IRF540，开关管并联电容为独石电容0.1μF，开关管驱动频率为45.3 kHz，死区时间为0.4μs，推挽变压器采用EI30型铁氧体磁芯，变压器匝数比为3∶3∶5，原边发射线圈电感值为115μH，补偿电容为0.33μF，副边接收线圈电感值为224μH，补偿电容为0.1 μF，原副边线圈互感为96μH，互感系数为0.6，整流管为BYW76，滤波电容为220μF，负载电阻为100Ω，输入电压为DC24V。

实验中采用SG3525来产生两路互补驱动信号，为增强驱动能力，两路信号接高速MOSFET驱动芯片IXDN404；图7是负载为100Ω时的变换器工作波形图。

图7中，从上到下依次为开关管漏源极间电压波形、开关管驱动波形、原边发射线圈电流波形和负载两端电压波形。由于系统为SP结构，拾取端的反射阻抗带有容抗部分，此容抗会影响到原边的谐振频率，因此本系统的工作频率会比系统的固有频率要高出10k左右。

图8、图9分别为开关管Q1开通时和关断时漏源极电压和驱动电压波形放大图，从图8可看出，当开关管开始工作时，其DS两端电压已经下降为零，实现了零电压开通。从图9可看出，当驱动电压变为零时，DS两端电压逐渐从零开始上升，实现了零电压关断。从实验波形上可看出，仿真和实验符合得非常好。

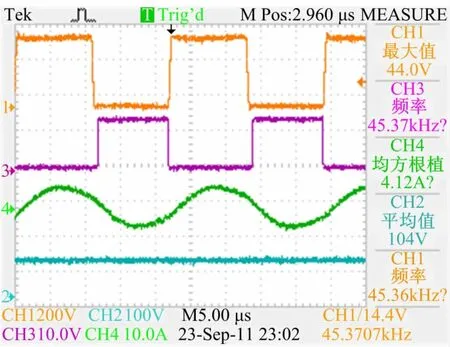
图7 变换器工作波形图Fig.7 Converter operating waveforms

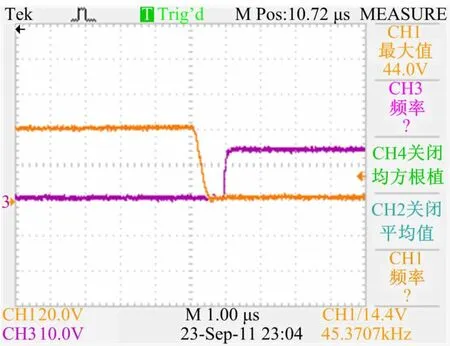
图8 开关管开通时漏源极两端电压波形图Fig.8 Voltage waveforms of drain－source as switch turning on

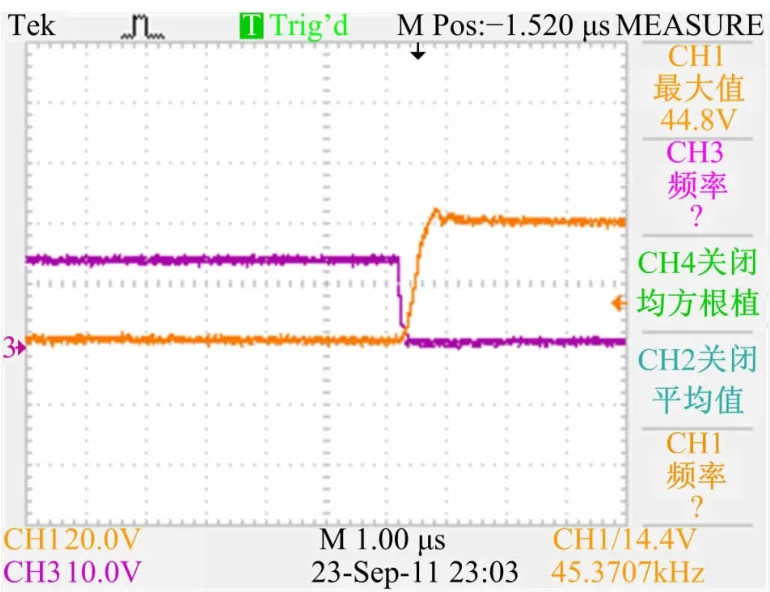
图9 开关管关断时漏源极两端电压波形图Fig.9 Voltage waveforms of drain－source as switch turning off

为验证负载在轻载和重载条件下变换器的软开关特性，在输入电压和驱动频率不变的条件下，令负载从25Ω变化到200Ω，随着负载变重，系统的输出效率先上升然后逐渐下降，当负载为200Ω时变换器开始失去软开关特性，但此时效率仍在80%以上，其中负载为100Ω时效率最高，达到了87%，输出功率接近110W。加入副边线圈后，线圈参数以及固有谐振频率都会发生改变，此时测得原边电感为87μH，互感为21 μH，根据式（10）计算出负载为173Ω时变换器失去软开关特性，理论值与实际值基本符合。研究结果表明该ICPT变换器可工作在软开关条件下，具有电路简单、传输效率高的特点。

5 结束语

通过引入推挽变压器，利用变压器的输出作为ICPT系统谐振网络的驱动源，在不增加电压过零点检测电路的基础上实现了变换器的软开关工作。分析了软开关的工作原理，给出了软开关工作需满足的条件，针对推挽变压器，给出了使系统稳定的变压器匝数比边界条件。仿真和实验结果表明，此变换器适用于原边为串联补偿结构的ICPT逆变拓扑，具有软开关实现简单、易于驱动、传输效率高的特点。本文所提出的软开关变换器在轻载条件下会失去软开关特性，如何扩大变换器的软开关工作范围需要进一步研究。

［1］Boys J T，Green A W.Inductively coupled power transmission concept－design and application［J］.The Institution of Professional Engineers New Zealand Transmissions，1995，22（1）:1－9.

［2］Boys J T，Covic G A，Green A W.Stability and control of inductively coupled power transfer systems［J］.IEEE Proceedings on Electric Power Applications，2000，147（1）:37－43.

［3］Kim Jin－wook，Son Hyeon－chang，Kim Kwan－ho，et al.Efficiency analysis of magnetic resonance wireless power transfer with intermediate resonant coil［J］.IEEE Antennas and Wireless Propagation Letters，2011，10（1）:389－392.

［4］Si Ping，Hu Aiguo Partick，Malpas Simon，et al.A Frequency control method for regulating wireless power to implantable devices［J］.IEEE Transactions on Biomedical Circuits and Systems，2008，2（1）:22－29.

［5］Cheon Sang－hoon，Kim Yong－hae，Kang Seung－youl，et al.Circuit－model－based analysis of a wireless energy－transfer system via coupling magnetic resonances［J］.IEEE Transactions on Industrial Electronics，2011，58（7）:2906－2914.

［6］Hu A P，Hussmann S.A phase controlled variable inductor designed for frequency stabilization of current fed resonant converter power supplies［C］∥Proceedings of the 6th International Power Engineering Conference，2003:175－180.

［7］Boonyarnate I，Mori S.A new ZVCS resonant pushpull DC／DC converter topology［C］∥Applied Power Electronics Conference and Exposition， Dallas，2002:1097－1100.

［8］张辉，邓嘉，马皓.一种双变压器串联谐振软开关推挽电路［J］.电力电子技术，2008，42（6）:28－35.Zhang Hui，Deng Jia，Ma Hao.A double－transformer series resonant soft－switching push－pull circuit［J］.Power Electronics，2008，42（6）:28－35.

［9］马运东，阮新波，严仰光.电压箝位ZVS推挽三电平直流变换器［J］.东南大学学报，2007，37（4）:623－628.Ma Yun－dong，Ruan Xin－bo，Yan Yang－guang.Voltage clamping ZVS push－pull three－level converter［J］.Jouranl of Southeast University，2007，37（4）:623－628.

［10］Tang C S，Sun Y，Su Y G，et al.Determining multiple steady－state ZCS operating points of a switchmode contactless power transfer system［J］.IEEE Transactions on Power Electronics，2009，24（2）:416－425.

［11］Hu A P.Selected resonant converters for IPT power supplies［D］.Auckland:The University of Auckland，2001.

［12］武瑛，严陆光，徐善纲.新型无接触电能传输系统的稳定性分析［J］.中国电机工程学报，2004，24（5）:63－66.Wu Ying，Yan Lu－guang，Xu Shan－gang.Stability analysis of the new contactless power delivery system［J］.Proceedings of the CSEE，2004，24（5）:63－66.

［13］Wang Chwei－sen，Covic Grant A，Stielau Oskar H.Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems［J］.IEEE Transactions on Industrial Electronics，2004，51（1）:148－157.