传递矩阵法在结构振动响应分析中的应用

武 鹏

（中国航空工业集团公司沈阳发动机设计研究所，辽宁沈阳110015）

0 引言

经典传递矩阵法是20 世纪20 年代建立起来的用于研究弹性构件组成的一维线性系统振动问题的方法。 经过多年的发展和完善，已经可以用于求解多圆盘轴的扭转振动问题、梁的弯曲振动模态、轴的横向振动问题、系统的静态响应和扭矩载荷响应问题、以及一维结构的振动特性分析和复合梁的振动特性等结构动力学问题。 并且，由于传递矩阵法建模灵活、计算效率高等优点，已在包括光学、声学、电子学、机器人学、机械、兵器、航空、航天等诸多现代工程技术领域中得到了广泛应用[1]。

应用传递矩阵法进行分析的一般步骤为：1）结构离散化；2）建立系统传递矩阵；3）特征方程求解。

1 结构离散化

航空发动机低压转子结构简化模型见图1：

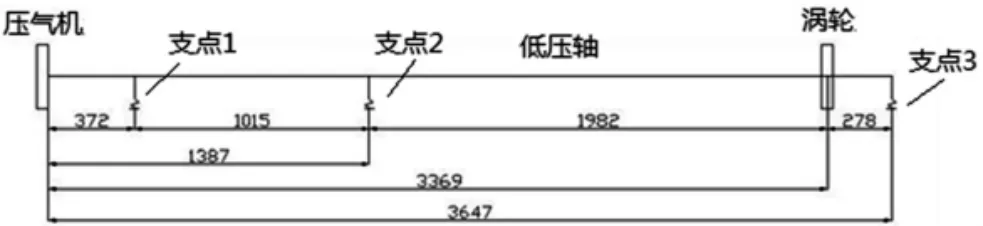
图1 低压转子结构简化模型

其主要组件为压气机、涡轮和低压轴。 低压转子通过前、中、后3个支点与发动机转子系统相连[2]。

将该结构进行离散化处理[3－5]，并将各支点简化为线弹性体后，得到图2 所示模型。

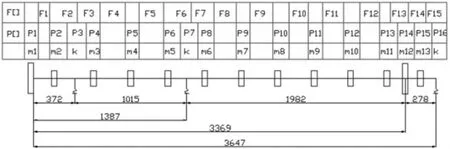
图2 离散化模型及节点编号

离散化处理后， 整个低压转子的质量将被转换为分布式质量节点。 表1 给出了离散化后各质量节点的质量分布情况。

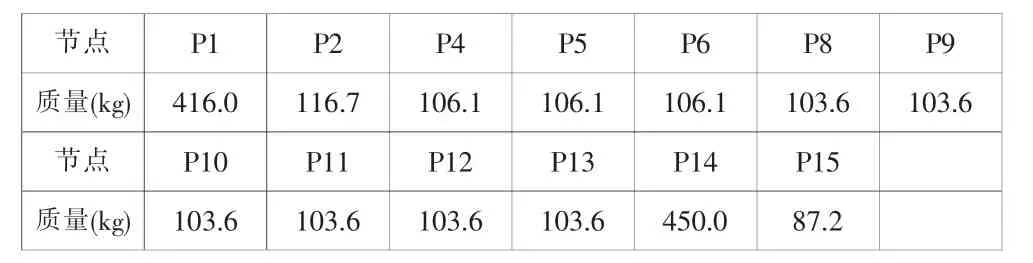
表1 模型质量分布

2 建立系统传递矩阵

将连续结构进行离散化处理后，实体结构将被简化成等刚性无质量梁单元及分布质量点。

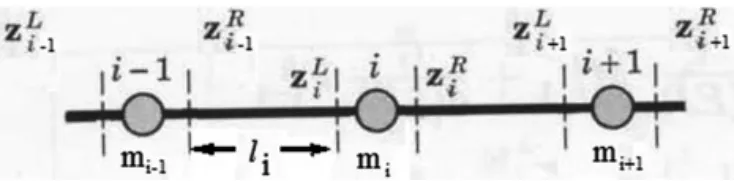
图3 梁单元及分布质量点[6]

如图3 中所示，梁单元位于相邻的两个质量点i-1 和i 之间，长度为li。

无质量悬臂梁的受力及变形如图4 所示。

图4 中，w 为挠曲变形量，φ 为挠曲变形角度；V 为切向力，M 为弯矩。

由梁单元两端受力平衡条件可得出如下方程：

工业视频内窥镜检测设备主要由光导纤维、插入管和视频成像系统组成，从而实现对管材内部视场范围内的监视、记录、存储和图像分析。

应用基本梁变形计算公式可得如下方程：

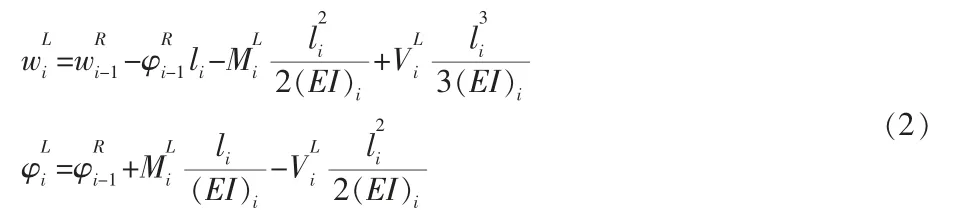
将节点jL和节点j-1R之间受力及挠曲变形关系用矩阵形式表示为：

分布质量点mi两端的无质量梁间，梁的挠曲变形、挠曲角度及弯矩时连续传递的，由此可得:

当分布质量点处于振动状态时，会产生与质量和振动角速度相关的内力，如图5 所示，这将导致节点两端的无质量梁间切向力不连续。

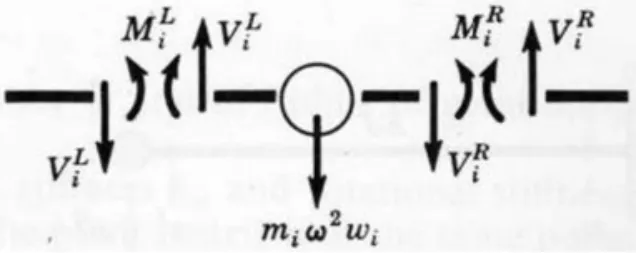
图5 自由状态下分布质量单元受力示意图[6]

此时，由力平衡方程可得：

将其转化为矩阵形式，表示为：

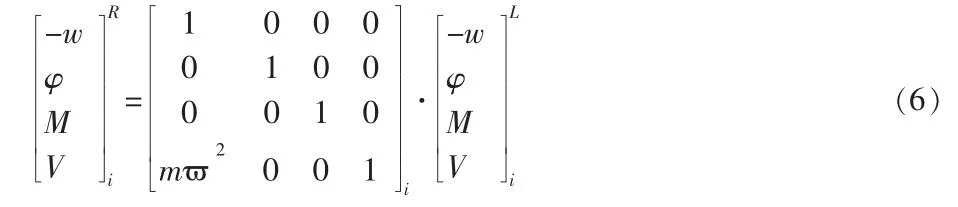
当梁支承在弹簧上时（图6），可得另一种节点传递矩阵。

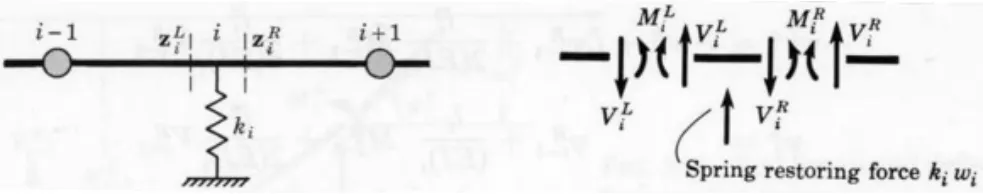
图6 弹性支承上的梁[6]

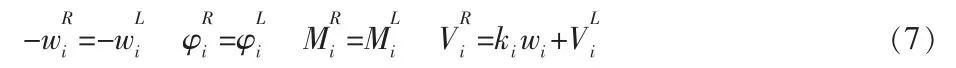
转化为矩阵形式为：

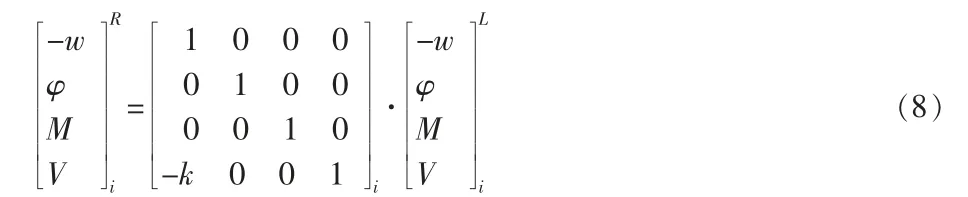
下一步是消除中间节点向量并选择频率因子。

将关系式（3）、（6）、（7）应用于整个转子，可得：

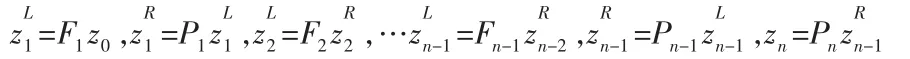
从而得出转子两端的节点向量之间的关系式：

将方程式（9）以矩阵形式表示为：

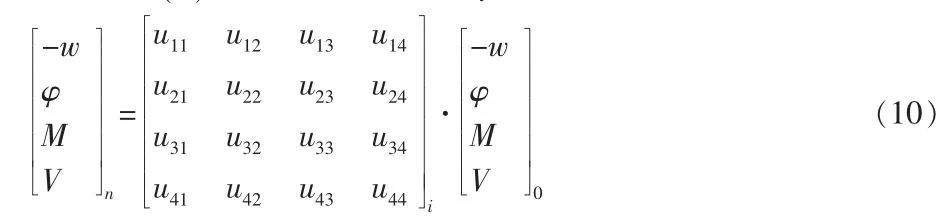
然后将边界条件带入方程式（10）以求得频率因子。

简支梁两端的边界条件为：

wn＝0，Mn＝0，w0＝0，M0＝0

3 特征方程求解

以转子转速做为变量，在不同刚度参数下对特征值进行求解。 在某一给定刚度下转速在0RPM～10000RPM 区间内，对特征值的计算结果如图7 所示。

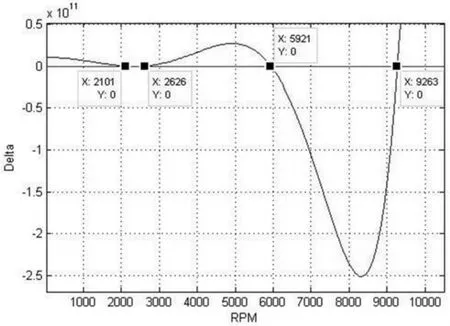
图7 给定刚度下临界转速计算结果(Matlab)

在图7 中，给定的转速区间内，特征值为“0”的点有4 个，这4 个“0”点对应的转速即为在此支承刚度下转子的临界转速。通过改变支承刚度，得到如下结果：

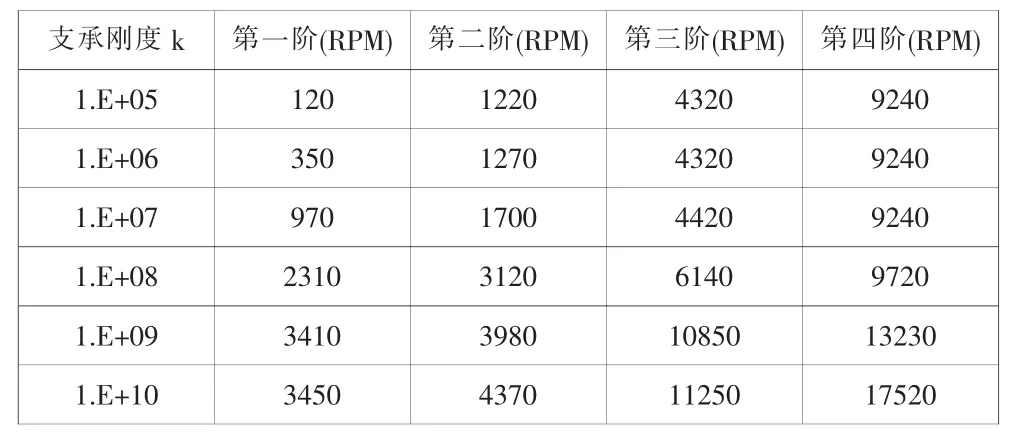
表2 模型临界转速

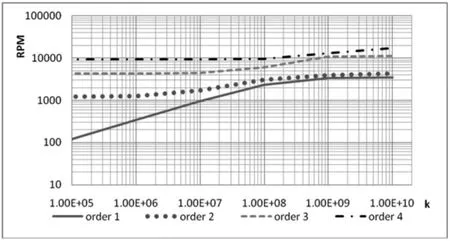
图8 转子临界转速

如图8 中所示，此模型在0RPM～20000RPM 转速范围内共存在四阶临界转速，随支承刚度变化，各阶临界转速呈现以下变化趋势：

1）K＜1.0×107N/m 时，第一阶和第二阶临界转速随支承刚度上升而逐渐上升，第三阶和第四阶临界转速基本保持不变；

2）1.0×107N/m＜K＜1.0×109N/m 时， 各阶临界转速都随支承刚度增加而上升；

3）1.0×109N/m＜K 时，前3 阶临界转速趋于稳定，第四阶临界转速仍随支承刚度增加而增加。

4 小结

本文以发动机低压转子为例， 建立了发动机转子离散化模型，通过求解系统传递矩阵得出转子在不同支承刚度下的临界转速。在计算中未考虑风扇轴与涡轮轴间套齿联轴器、轴承阻尼特性和陀螺力矩等影响， 并且为简化计算步骤将三个支点的支承刚度设置为了相同值。在后续的深入研究过程中， 将以发动机的整个转子系统为分析对象，通过离散化处理，建立整个转子系统的传递矩阵，以求得转子-支承-机匣的复合振动响应特征。

［1］芮筱亭，戎保.多体系统传递矩阵法研究进展[J].力学进展，2012,42(1)：4-17.

［2］Rolls-Royce Ltd. The Jet Engine[M].6thedition, Rolls-Royce, 2005.

［3］Pilkey W D, Chang P Y. Modern Formulas for Statics and Dynamics [M]. New York: McGraw-Hill Book Company, 1978.

［4］蒋书运，陈照波，须根法，等.用整体传递矩阵法计算航空发动机整机临界转速特性[J].哈尔滨工业大学学报，1998,30(1):32-38.

［5］Lee U. Vibration analysis of one-dimensional structuresusing the spectral transfer matrix method[J]. Engineering Structures, 2000,22: 681-690.

［6］Pestel, Eduard C., Matrix Methods in Elastomechanics[M].McGraw-Hill, 1963.