微型汽车发动机悬置系统优化设计方法研究

梁静强，杨连波，吕俊成

（上汽通用五菱汽车股份有限公司，广西柳州 545007）

1 引言

微型汽车作为一种低价格、低油耗、低污染的经济实惠型汽车，近年来已经成为发展速度最快的行业之一。发动机悬置系统（以下简称悬置系统）作为汽车振动系统的一个重要子系统，在改善汽车平顺性和舒适性方面起着重要作用。近十年来，国内外众多学者在振动解耦方面对悬置系统进行了研究［1，2，3，4］。在应用这些研究结果过程中发现：（1）优化后的刚度在实际结构中难以实现；（2）在进行悬置系统设计时，悬置类型以及大致结构形式就已确定。这些约束条件在设计前期不能得到充分考虑，往往会导致优化结果不符合实际。本文以结构可行性为导向，基于能量解耦理论，以能量解耦率、频率分布范围为目标，悬置刚度和角度为变量，弹性轴与扭矩轴之间的夹角为评价标准，提出一套适用于微型汽车的悬置优化设计方法。

2 优化方法

微型汽车性能有着自己独特要求，悬置系统也不例外。基于微型汽车的特点，本文以固有频率的合理配置理论、能量解耦理论和弹性轴理论为基础，并通过多次的试验对比验证，对微型汽车悬置性能提出以下几点约束要求：（1）使悬置系统（包括动力总成）z 轴平动和绕x 轴转动的固有频率低于15Hz；（2）悬置系统最高频率均低于17Hz（避免怠速时共振）；（3）各模态频率的间隔不小于1Hz；（4）z轴平动和绕x 轴转动具有较高的能量解耦率（80%以上）；（5）对于扭矩轴和弹性轴的夹角，至少小于3°。

微型汽车设计空间小，设计约束多。对于悬置的开发，输入条件往往大部分已经限定，而不能根据性能优化的需要任意改动输入条件。为节省成本，供应商往往已经确定，悬置类型、大致结构已经确定，动力总成的位置也已经限定在一个很狭小的空间范围内。微型汽车悬置刚度优化须满足这些限定条件。按一般优化方法优化后，悬置参数往往在实际应用中不能实现。笔者提出一套可适用于微型汽车悬置开发的优化方法。

2.1 建立材料库

在悬置前期设计阶段，优化后的悬置刚度在实际结构中却难以实现。鉴于此，需要收集供应商提供的各种材料试验数据，建立相对应橡胶本构模型库。以结构可行性为导向对各种可能用到的结构进行分析，找出合理的刚度比。

为获取不同材料不同结构的悬置各向刚度比，通常需要进行大量试验。本文采用非线性有限元方法，以常用的Mooney-Rivlin 橡胶本构模型，对悬置结构进行仿真模拟计算。

应用Mooney-Rivlin 橡胶本构模型，可模拟不同材料的力学性能，通过有限元分析方法，可计算出不同形状不同尺寸的悬置结构三个主方向的刚度比。刚度比计算流程如图1 所示。

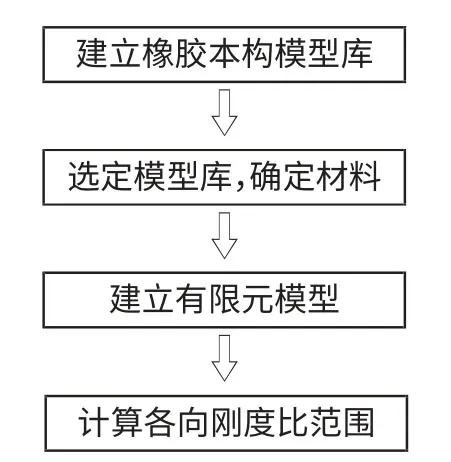
图1 刚度比计算流程

2.2 刚度优化

根据已经选定的供应商，选择相应模型库；根据选定的悬置结构，建立变几何参数的有限元模型；变换几何参数进行试验设计（DOE），计算在各种可能的几何形状下，悬置三个方向间的刚度比值范围，以此作为刚度设计的约束条件；基于固有频率合理配置理论，对悬置系统的固有频率进行约束；以悬置的刚度、位置和角度为优化变量，以悬置系统的解耦率和弹性轴与扭矩轴TRA的夹角为目标，对悬置系统进行优化。整个过程如图2 所示。

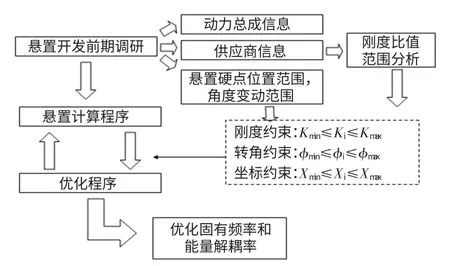
图2 悬置开发流程图

3 实例分析及评价

3.1 数模及参数

图3 悬置结构图

悬置系统匹配和优化所需的相关参数可以通过相应的测试和计算获得。某微车匹配I4 四冲程汽油机，怠速转速为850r/min，悬置系统相关参数如表1～表5 所示，结构已确定为方块橡胶，如图3 所示。其中，整车坐标系x 轴方向定义为从车头到车尾方向，z 轴垂直向上；发动机坐标系x 轴方向定义为从发动机的前端指向变速器方向，z 轴为活塞运动方向由油底壳指向缸盖。

表1 某微车动力总成系统质量及转动惯量

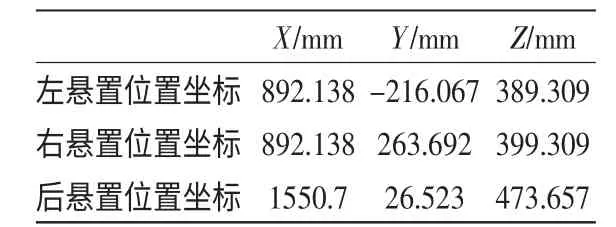
表2 悬置点在整车坐标系中的位置坐标

3.2 优化设计

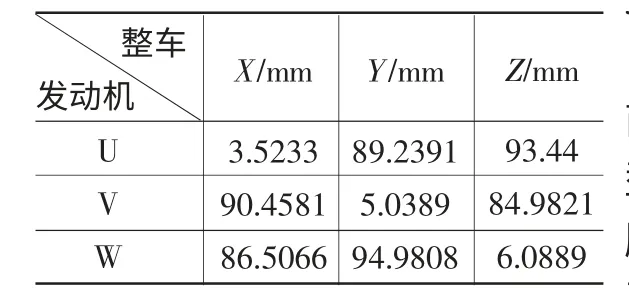
表3 发动机坐标系与整车坐标关系

表4 悬置动刚度

3.2.1 刚度比分析

根据选定的供应商，选定相应的材料模型；根据确定的方块橡胶结构，建立有限元模型（图4），并进行刚度计算，整理出该类型结构的可能刚度比范围。左右悬置刚度整理结果如图5 所示，后悬置刚度整理结果如图6 所示。

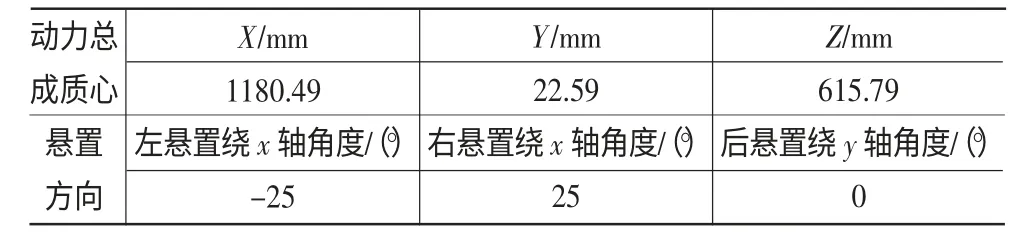
表5 其他参数

图4 橡胶块有限元仿真

结果表明，对于左右悬置：x 轴向刚度与y 轴向刚度比值均大于4；z 轴向刚度与y 轴向刚度比值大部分落在0.9～1.1 之间。对于后悬置：x轴向刚度与y 轴向刚度比值大部分落在在0.5～2 之间；z 轴向刚度与y 轴向刚度比值大部分落在2.4～5 之间。

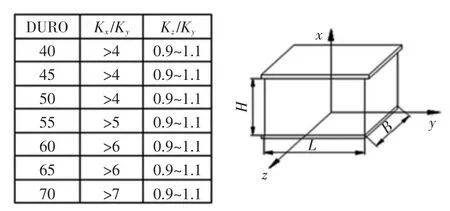
图5 左右悬置刚度范围

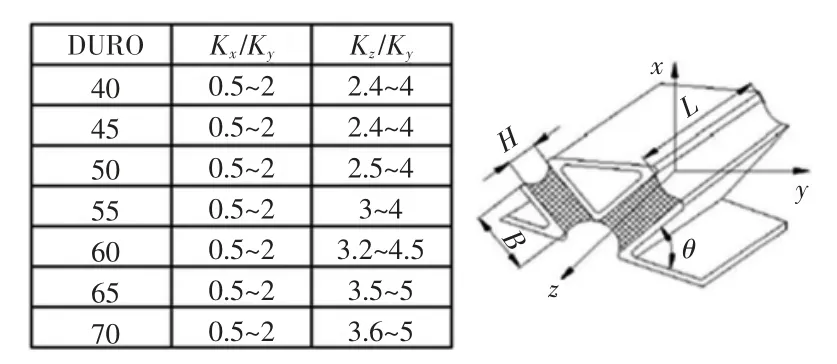
图6 后悬置刚度范围

3.2.2 约束条件及优化目标

由刚度分析结果，对悬置刚度约束确定为：左右悬置：Kx/Ky＞4，0.9＜Kz/Ky＜1.1；后悬置：0.5＜Kx/Ky＜2，2.4＜Kz/Ky＜5。

对于固有频率的约束：5Hz＜f＜17Hz；各阶次间固有频率的间隔不小于1Hz。

优化目标：在roll 和bounce 方向的解耦率需要大于80%，各向解耦率越大越好；扭矩轴和弹性轴的夹角越小越好。

根据该款车的总布置规划，对悬置系统进行约束。（1）对于左右悬置向内转角约束：5°＜θ＜40°，图6为转角θ 示意图。（2）对于悬置硬点位置的约束：左右悬置位置（相对于整车坐标系）在x、y 方向变动＜|5|mm 以内，在z 方向＜|15|mm；后悬置在x、z 向＜|50|mm，y 向＜|20|mm。

3.2.3 优化设计

对原系统进行性能计算，性能效果不理想。roll 和bounce 方向的解耦率低于80%，最低频率小于5Hz，第三阶次频率8.36Hz 与第四频率阶次频率8.60Hz 非常接近，配置不够合理；扭矩轴与弹性轴夹角为4.9°，夹角较大。以上所述均不符合悬置系统的NVH 性能要求，需要优化。

悬置动刚度优化后结果如表6所示，其解耦率见表7。优化后系统的固有频率范围在5～17Hz之间分布，最低频率大于5，各阶次间固有频率的间隔满足不小于1Hz的要求；解耦率在roll 和bounce 方向的解耦率均大于80%；扭矩轴与弹性轴夹角从原来的4.9°减小到0.5°，优化结果符合设计要求。

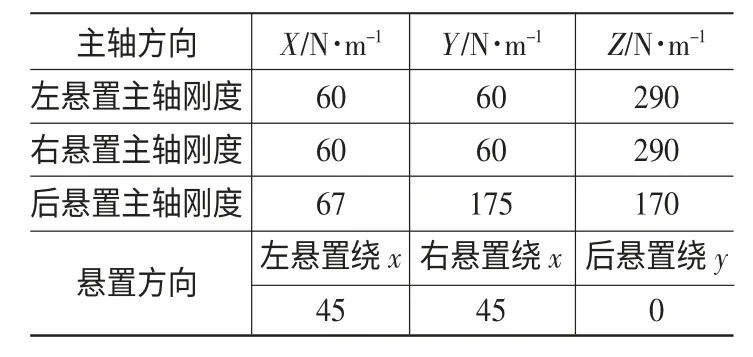
表6 优化设计的悬置动刚度和方向

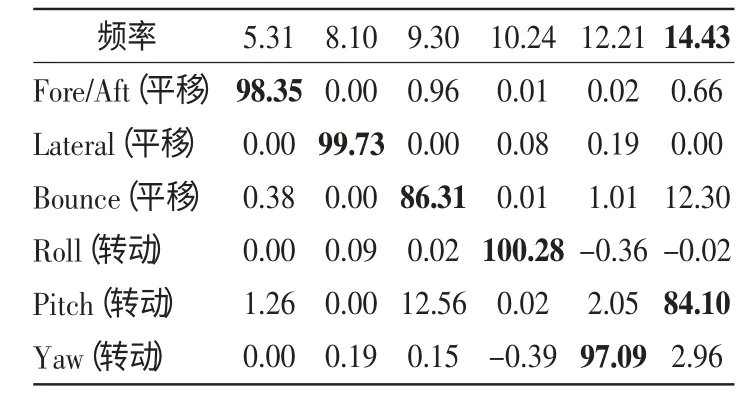
表7 优化设计的悬置系统解耦率 /Hz

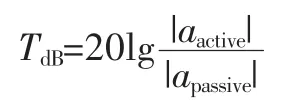
其中，aactive为发动机侧悬置支架处测得的加速度幅值；apassive为车架侧悬置支架处测得的加速度幅值。

一般认为振动的衰减率应该在20dB 以上，隔振器具有良好的隔振效果［6］。

试验证明，优化后加速度的传递率满足大于20dB的NVH 要求。

4 结论

（1）根据此套优化方法进行悬置系统优化设计，可以快速方便设计出一款适合于微型汽车领域的悬置系统。

（2）应用该方法，可以在设计初期就能考虑到结构加工的可行性，减少返工设计时间，大大节省开发成本。

（3）该方法基于模态能量解耦理论对悬置参数优化，隔振效果满足微型汽车NVH 要求。

［1］JOHNSON S R.Computer Optimization of Engine Mounting Systems［C］//SAE paper 790974，1979.

［2］JEONG T，et al.Analytical methods of decoupling the automotive engine torque roll axis ［J］.Journal of Sound and Vibration，2000，234（1）:85-114.

［3］方锡邦，汪佳.轿车动力总成悬置系统三维动力学模型的建立及优化［J］.阜阳师范学院学报，2004，21（2）：45-56.

［4］侯勇，赵涛.动力总成悬置系统解耦设计［J］.汽车工程，2007，29（12）：1094-1097.

［5］沈慧，李志远.内燃叉车发动机的隔振试验与分析［J］.工程机械，2008，39（5）：27-31.

［6］吴炎庭，袁卫平.内燃机噪声振动与控制［M］.北京：机械工业出版社，2005.