基于模糊控制的主动型配电网潮流计算方法研究
宋三女胡新参鲁籍元李汉成
(1.北京市电力公司,北京 100031;2.中国农业大学信息与电气工程学院,北京 100083)
潮流计算是配电网规划、运行和控制的重要手段。分布式电源和低压微电网接入配电网之后,将改变传统配电网的无源网络特点,使其成为有源网络,对配电系统的潮流走向、电压分布、网络损耗、调度运行等各方面都会产生重要影响。配电网从传统的自然分布型潮流向主动调控型潮流的转变,对我们改进原有的潮流计算方法提出了新的课题。因此,有必要在分析DG并网模型特点的基础上,对含有PV等多类型DG节点的复杂配电网稳态潮流进行研究,找到收敛高效的一般性实用计算办法。文献[1]在直接法的基础上,采用灵敏度矩阵的补偿算法对包含不同类型DG的配电网潮流计算进行了研究。与N-R法、高斯法和直接法相比,前推回代法具有收敛性好、占用内存少、不需要Jacobi矩阵、容易编译等优点,在配电网潮流计算中被广泛使用[2]。但是该方法只能处理平衡节点和 PQ型节点,对于现实中 PV等多种类型DGs其适用范围就受到限制[3-7]。
综上所述,传统的配电网潮流计算方法在处理含DG的主动型配电网时,由于传统的配电网潮流计算中一般只有平衡节点和PQ节点两种类型,但在含 DG的配电网潮流计算中,并不能完全将所有的DG节点一律当成PQ节点来处理。根据DG接入配电网的方式,其可作为PQ、PI或PV节点处理,特别是 PV节点的接入给配电网潮流计算和收敛带来一定难度[8-9]。
针对上述问题,在研究分析各种典型分布式电源模型的基础上,本文提出了基于模糊控制的主动型配电网潮流计算方法,该方法可用于多PV节点的配电网潮流计算。算法利用模糊控制理论等现代控制技术,提高算法计算的快速性和收敛性,以满足主动型配电网潮流的一般性计算要求。
1 分布式电源简介
在稳态分析中的分布式电源所在节点可分为3类:PQ节点、PI节点、PV节点。
1.1 PQ节点
给定节点注入或者流出功率的节点称为PQ节点。这种类型的DG与PQ型负荷相比,只是功率流向相反。因此,在处理此类DG时,只需改变功率的符号即可,无需做特殊处理。值得指出的是,低压微电网如果运行在受电方式则与负荷节点相同,如果运行在向电网馈电方式,则与 DG相同。此类节点的功率为

式中,P、Q分别为节点有功和无功功率,流出节点为正;PS、QS分别为给定发电机输出有功和无功功率。
1.2 PI节点
通过电力电子功率变换器并网的分布式电源,采用电流控制模式时其输出有功和注入配电网的电流是恒定,称为PI节点。在潮流计算过程,此类发电机输出的无功功率可以通过每次迭代得到的电压、恒定的电流幅值和有功功率计算得出

式中,Q(k)为第k次潮流迭代的PI节点无功功率;U(k-1)为第k-1次潮流迭代得到的电压值;Is为给定输出电流。
1.3 PV节点
微型燃气轮机、有励磁调节的风力发电机以及采用恒电压控制功率变换器接入的DG均可视为PV型分布式电源。基于 PQ分解和或牛顿法的潮流计算方法都是由给定条件直接写出方程然后求解。高斯潮流计算方法在潮流计算的每次迭代过程中,需要对于PV节点i的注入无功功率进行计算,令


也就是,在PV节点的迭代过程中,须不断修正为了维持节点电压恒定所需的无功功率,当修正值超过所给出的限额时,PV节点将向PQ节点转化,届时按照式(5)处理即可。
2 模糊控制系统
模糊控制以模糊集合论、模糊语言变量及模糊逻辑推理为基础,其核心是模仿人的思维决策去控制复杂性、不确定性对象的一种控制方法,模糊控制属于智能控制的范畴,尤其是对于无法获取精确数学模型的被控对象,模糊控制是一种有效的控制方式。目前,模糊控制已成为智能控制的一种重要分支。模糊控制系统的基本结构如图1所示。

图1 模糊控制系统
其中:①模糊化:将输入的精确值进行尺度变换,转化为需要的模糊值;②模糊规则库:包含了具体应用领域中的知识和要求的控制目标;③模糊推理:模糊控制器的核心,它是基于模糊逻辑中蕴含关系及推理规则来进行的;④清晰化:将模糊量进行尺度变换,转化为实际的控制量[10]。
3 基于模糊控制的PV节点注入无功功率修正方法
采用模糊控制技术对潮流计算中PV节点进行处理,由每次迭代得到的节点电压与PV节点给定电压之差作为模糊控制器的输入量,输出量为该节点无功功率的修正量。在常规配电网潮流计算程序中嵌入PV节点处理模块即可,因此下面主要介绍基于模糊控制器的PV节点的无功功率的修正方法。
3.1 模糊控制器建模
1)输入输出模糊向量
设x是潮流计算第k次迭代中,某PV节点电压偏移量ΔV的清晰值:

式中,Vk为潮流计算第k次迭代节点电压值,Vs为PV节点给定电压值。
设计模糊控制器输入量节点电压偏移的实际值的变化范围为[-0.1Vs,0.1Vs]、清晰值x的量化论域X为[-6,6]。输入量x的模糊词集定义为

除了将零子集划分为正负两个之外,量化论域X上模糊子集Ti的分布为均匀分布。设计采用高斯形隶属度函数,即

式中,i为模糊子集序号。当i=1,2,…,8时,参数ai和bi的取值见表1。

表1 隶属度函数参数表
将所有输入变量清晰值代入式(7)中得输入语言赋值表2。
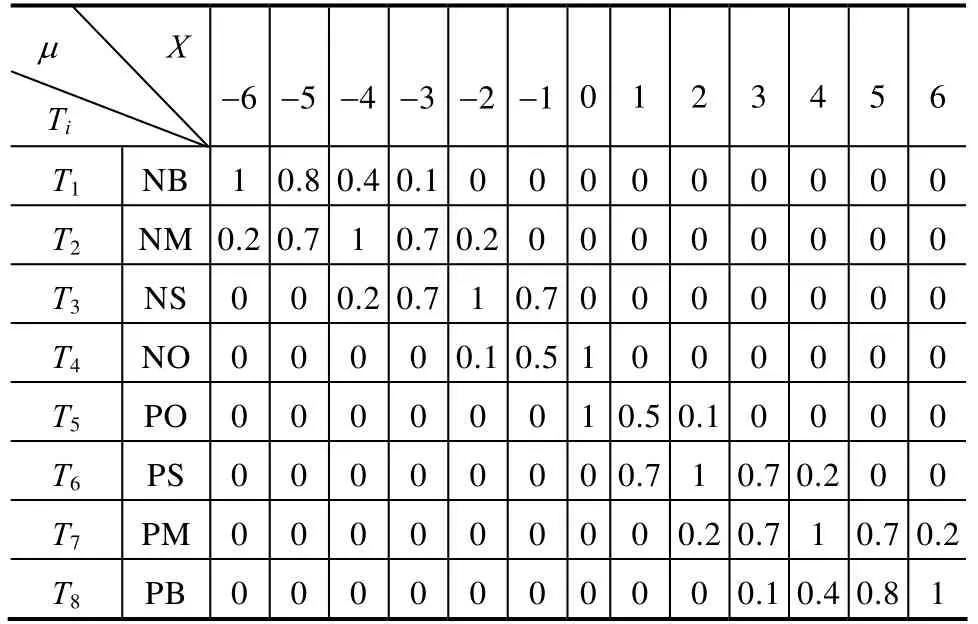
表2 输入语言赋值表
同样地,z是潮流计算第k次迭代中,某PV节点的无功修正量ΔQ的清晰值:

式中,Qk和Qk-1分别为第k和k-1次迭代PV节点注入的无功功率。
设模糊控制器输出节点注入无功功率第k次迭代修正量的实际值变化范围为,设计清晰值 z的量化论语 Z为[-6,6]。输入量z的模糊词集定义为

除了将零子集划分为正负两个之外,量化论域Z上模糊子集Oi的分布为均匀分布。将所有输出变量清晰值代入式(6)得输出语言赋值。
设模糊控制器输出变量的清晰值 z对应各量化等级的隶属度分别为μo1,…,μo8,则控制器输出模糊向量定义为

2)模糊推理机
设计模糊控制系统的模糊推理机,包括确定输入模糊集(模糊向量)与语言模糊集(模糊向量)的模糊蕴含关系矩阵R和Min-Max(Mamdani)法。
PV节点无功修正量与节点电压偏移量控制的逻辑关系为“如果节点电压高于给定值,则无功输出减小;如果节点电压低于给定值则无功输出量增大”。相应 PV节点无功修正单输入单输出模糊控制器的模糊规则库见表3。

表3 模糊规则表
表3中8条模糊控制规则用语言来描述为
R1:如果节点电压ΔV负向偏离很大(x是NB),则无功修正量ΔQ正向调节量大(z是PB)
R2:如果节点电压ΔV负向偏离中等(x是NM),则无功修正量ΔQ正向调节量中(z是PM)
……
R8:如果节点电压ΔV正向偏离很大(x是PB),则无功修正量ΔQ负向调节量大(z是NB)
遍历模糊规则库表3中所有输入输出,用Min-Max(Mamdani)法得到PV节点无功修正量关于节点电压偏移量模糊蕴含关系矩阵为

3.2 计算步骤与方法
基于模糊控制的PV节点无功修正量计算模块计算步骤如下:
步骤Ⅰ:模糊化
以式(6)所得ΔV作为实际物理系统输入量,Δ V的变化范围为[-0.1Vs,0.1Vs],清晰值x的量化论域为[-6,6]。则输入模糊量为

将x用四舍五入的方法量化到相应的量化等级,得到输入变量的清晰值{∈[-6,6]and x∈Z}。
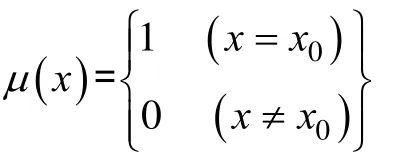
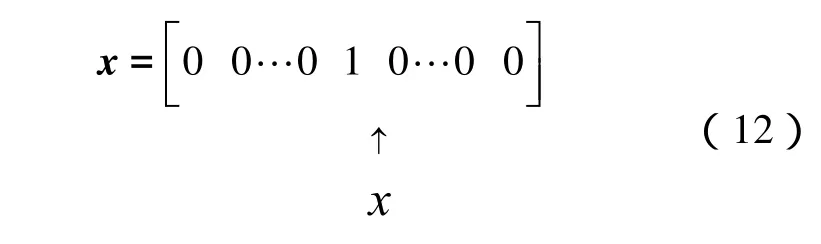
步骤Ⅱ:模糊推理计算求输出模糊向量推理计算式:

式中,x为式(12)得到的输入模糊向量,R为式(10)定义的蕴含关系矩阵,待求输出模糊向量,运算“°”采用Min-Max方法。
步骤Ⅲ:计算输出向量的清晰值(解模糊)
将模糊输出向量z用最大隶属度法取μ(z)最大时对应的z为其清晰值,即

步骤Ⅳ:计算实际无功修正量
模糊控制器输出节点注入无功功率第k次迭代修正量实际值的变化范围为,,清晰值z的量化论域Z为[-6,6]。则实际无功修正量为

在运用上述模糊方法计算PV节点注入无功修正量时,量化论域Z可继续细化,取[-n, n](n为实数),以得到更加精确的无功修正量。
4 算例验证
4.1 算例介绍
为了验证上述算法的有效性,本文对图2所示IEEE33节点配电系统[11]做了改变,在不同位置接入不同类型的DGs,分别采用基于模糊控制的配电网潮流算法和牛顿法进行计算,收敛精度要求为ε =10-5。设计了两种计算场景,设计了两种计算场景,场景1为安装两台 PV型分布式电源;场景 2为安装PV型和PQ型分布式电源各1台。

图2 IEEE 33节点系统拓扑结构
4.2 计算结果对比
场景1:在母线4、2处各接入一个PV型DGs,有功和电压值分别为:P(4)=0.0042、U(4)=1.02;P(2)=0.0034、U(2)=1.02。两种方法计算结果的相对误差如图3所示。模糊法的计算时间较快,为25.11ms。相对误差计算公式为式(16),电压平均相对误差为-0.00012%,相角平局相对误差为0.002607%。


图3 场景1条件下两种方法误差
场景2:在母线5处接入一个PQ型DGs,注入功率为:S(5)=0.0309+0.0057i;在母线3处接入一个PV 型DGs,有功和电压值分别为:P(3)=0.0034、U(3)=1.02。两种方法计算结果的相对误差如图4所示。模糊法的计算时间较快,为24.22ms。电压平均相对误差为0.000042%,相角平均相对误差为0.004751%。

图4 场景2条件下两种方法误差
4.3 结果分析
由上述两种场景仿真计算结果可以看出:
1)与牛顿法比较,基于模糊控制的潮流算法在全为PV分布电源、PV与PQ多种类型分布式电源接入的情况下,电压幅值的平均相对误差小于0.001%、电压相角的平均相对误差小于0.01%,最大误差发生在PV节点接入点附近,电压幅值相对最大误差为0.004%、相角最大相对误差为0.0088%。
2)基于模糊控制的潮流算法在场景1和场景2下的计算时间分别为25.11ms和24.22ms,相对牛顿法计算速度有较大的提高。
上述结果分析表明,本文提出的基于模糊控制的配电网潮流计算方法能够有效地处理含各种类型分布式电源,计算精度符合工程要求。
5 结论
本文在分析各种典型分布式电源并网模型特点的基础上,对主动型配电网稳态潮流计算方法进行了重点研究和实现,提出了含多 PV节点的配电网模糊控制潮流算法。该算法通过对模糊控制系统的研究,设计了适合处理含PV节点的潮流方法,有效地克服了前推回代法只适用于 PQ恒定型负荷的限制,扩展了它的适用范围。算例计算表明,模糊控制法在处理多PV型DGs上,具有编程简单、计算速度快、数值稳定性好、占用内存少等优点,是一个有效的配电网潮流算法。
[1]梁有伟,胡志坚,陈允平.分布式发电及其在电力系统中的应用研究综述[J].电网技术,2003,27(12):71-75.
[2]丁明,王敏.分布式发电技术[J].电力自动化备,2004,24(7).
[3]王建,李兴源,邱小燕.含有分布式发电装置的电力系统研究综述[J].电力系统自动化, 2005(29).
[4]申洪,王伟胜,戴慧珠.变速恒频风力发电机组的无功功率极限[J].电网技术, 2003, (11): 60-63.
[5]MORI H, SAKATANI Y. Application of Probabilistic(N-1) Security Assessment Technique to Distribution of IEEE/PES Transmission and Distribution Conference and Exhibition 2002, 2:739.
[6]OKUYAMAK, KATO T, SUEUOKI Y, et al. Improvement of Reliability of Power Distribution System by Information Exchange Between Distributed Generators Sharing of all DGs Information[J]. In:Proceedings of 2001IEEE Power Engineering Society Summer Meeting, 2001(1): 168-473.
[7]KIM T E, KIM J E. Vlotage regulation coordination of distributed generation system in distribution system[J].In: Proceedings of 2001 IEEE Power Engineering Society Summer Meeting,Vancouver:2001(1):480-484.
[8]孙健,江道灼,刘志华.基于前推回代的配电网潮流改进算法[J].电力自动化设备, 2004(3).
[9]楚冬青.基于叠加原理和前推回代法的10kV配电网合环潮流计算[J].企业科技与发展, 2010(10).
[10]CHEN T H, CHEN M S, HWANG K J. Distrib Vtion system power flow analysis-a rigid approach, 1991(03).
[11]THOMSON M, INFIELD D G.Network power-flowanalysis for a high penetration of distributed generation[J].IEEE Transactions on Power Systems,2007, 22(3): 1157-1162.

