基于一种组合方法的地下电缆载流量的计算及恢复

邢雅 李洪杰

（西安交通大学电气工程学院，西安 710049）

为了使地下电缆可靠地运行和高效的传输，目前主要采用两种方法来计算电缆的载流量。一种是基于国际电工委员会IEC 60287标准的热路分析法[1-3]。另外一种是数值计算方法，常用的数值计算方法有边界元法、有限差分法、有限容积法及有限元法[4-7]。在这些方法中有限元法能够方便的应对各种复杂的电缆敷设环境和边界条件，应用该方法能够更为有效和精确的计算电缆的载流量及热状态。

由于土壤热参数和周围环境温度是随着季节和地形变化的，从而使得电缆的载流量在较大的范围内变化。现代分布式光纤温度测量系统（DTS）的发展为实时测量地下电缆表面温度从而监测电缆的热状态提供了新的机会[8]。作为国家的电力公司，新加坡电力公司管理着整个新加坡的地下输电和配电线缆网络，其中最新的230kV电缆线路已经全部安装了DTS[9]。

本文基于DTS测量的电缆表面温度曲线，利用一种有限元数值计算方法与基于梯度的优化方法的组合方法估算出电缆周围土壤的热参数从而实现地下电缆载流量的实时评估。以实际应用的一条230kV/500MVA电缆线路为例，利用所提出的方法对其长期运行额定载流量及紧急过负荷载流量进行了精确的评估。最后，为了缓和电缆沿线的热点从而使得整个电缆线路的载流量能够得到较为显著地恢复，本文采用一种通过移除电缆沿线热点顶部填土的方法，利用大型通用有限元仿真软件进行三维仿真分析来证明其有效性。

1 土壤热参数的估算方法

1.1 估算方法

图1为两条不同传输容量的230kV电缆线路平面排列的敷设横截面图。一根DTS光纤被安装在500MVA线路中间相表面的E点，用来测量其表面温度。由图1可知，一旦电缆的结构、敷设环境和负载电流确定，那么电缆的温度分布只取决于周围土壤的热参数及土壤温度。也就是电缆表面E点的温度TE是土壤热阻率ρsoil、热扩散率δsoil、土壤温度Tsoil和时间t的函数。

图1 两条230kV电缆线路的敷设截面图

基于DTS测量温度曲线，电缆沿线热点可以很容易的被识别和定位。例如，图2为230kV/500MV·A线路电缆表面温度曲线以及最高温度点“A”。基于最高温度点处的电缆结构和安装信息，这些未知的参数x=(x1, x2,…, xn)=(ρsoil,δsoil,Tsoil)可以通过最小化如下的目标函数而被估算出来

式中，N为离散测量点的总数；T是温度测量的持续时间；Δt为测量的时间间隔；Tm(jΔt)为 E点的测量温度（图2）；TE(jΔt)为计算的E点的温度，该值需要利用有限元法和优化法的组合方法来得到。

图2 230kV/500MVA电缆线路表面温度曲线

估算过程中，整个计算场域土壤的热参数被看成均匀各向同性的。有了这个假设，那么土壤热阻率和热扩散率可以通过以下的经验公式联系起来[10]，即

利用式（2），未知参数减少为两个，也就是x=(ρsoil,Tsoil)，使得评估电缆热状态的过程更加简单。

1.2 优化算法

本文使用变尺度法（DFP算法）来最小化目标函数（1）[11]，每一个迭代步骤k的搜索方向可以写为

式中，xk为第k次迭代的参数向量。

式（3）中，目标函数F对第j个未知参数xj的偏导数可以写成

式（2）中的TE(t, x)没有关于未知参数xj的解析表达式。因此，式（4）中的微分项可以用其中心差分形式来表示，即

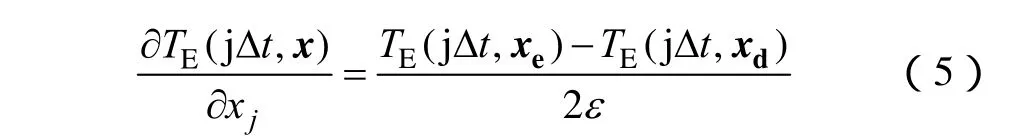
式中，ε为一个很小的扰动；xe=(x1, x2,…,xj+ε,...,xn)，xd=(x1, x2,…,xj-ε,…,xn)。

式（5）中，TE(jΔt,xe)和TE(jΔt,xd)可以使用有限元方法数值计算。

当满足以下两个条件后，优化过程终止。

（1）两次连续的迭代k-1和k中第j个未知参数xj的相对变化不大于10%。

（2）目标函数F的值不超过0.5℃。

2 电缆的温度场模型

图1所示的电缆敷设截面图可以简化为一个二维温度场，基本导热微分方程如下[12]

式中，x, y为空间坐标，单位为m；T为温度，单位为K；ρ为相应材料的热阻率，单位为K·m/W；δ为相应材料的热扩散率，单位为m2/s；t为时间，单位为s；Q为相应区域的产热率，包括电缆导体，绝缘层和护套，单位为W/m3，各部分的损耗可以通过IEC 60287标准给出的经验公式计算出。

图3所示为待研究的电缆热场域，选择以坐标原点“O”为中心，半径R=10m的半圆形为计算场域，为了简化计算，在半圆边界Γ上，边界条件为

图3 230kV电缆线路简化热场域

3 实例应用

本节介绍了一个典型的实例分析。所提出的研究方法被应用到评估一条安装有DTS的230kV/500MVA电缆线路的载流量，其安装截面图如图1所示。表1列出了230kV电缆的基本结构数据。

表1 两条230kV充油电缆的基本结构参数

地下电缆沿线由于敷设环境的变化会存在很多热点。然而，在所有的热点中，某些位置上的热点温度比其他所有热点的温度都要高，这个最高温度点决定了整个电缆线路的载流量。图2中点“A”为500MVA线路中温度最高点，因此，本文选择热点“A”处来评估 230kV/500MVA线路的载流量。图4为230kV电缆线路中“A”点的现场条件图，通过调查发现，热点“A”形成的主要原因有三个。首先，如图4所示，该位置在公路立交桥下方，使得雨水不能够浸润土壤，从而导致现场土壤非常的干燥；其次，该线路下方还存在另外一条250MVA的电缆线路，阻碍了500MVA线路的热量扩散。最后，如图1所示，电缆的轴向距离较近，只有0.25m，而制造商推荐的空间距离为0.3m。图5为使用Matlab离散后的场域。由于计算场域关于Y轴对称，因此只有一半的区域被剖分。

图4 热点“A”的现场环境图

图5 离散场域

3.1 土壤热参数的估算

图6所示为5天内记录的两条线路的负荷电流曲线、DTS所测量“A”处500MVA中间相电缆的表面温度曲线和计算温度。前三天的时间段里，利用测量的电缆表面温度数据和所提出的组合研究方法来最小化目标函数式（2），从而估算得到土壤的热参数为

利用估算的土壤热参数，电缆导体和表面的温度都可以被预测。图6中后两天计算的温度曲线均为预测的温度，可以看出，从第4天到第5天预测的表面温度与使用DTS测量的表面温度很好的吻合。

图6 5天内两条230kV电缆线路的负载电流、测量温度以及计算温度

3.2 载流量的评估

利用式（9）中估算的土壤热参数，电缆在正常连续负荷和过负荷条件下的最大允许运行电流关于时间的曲线可以很容易的被预测。

1）持续运行载流量

持续运行载流量表示在电缆导体温度不超过允许温度85℃时，电缆运行时的最大恒定负载电流。利用式（9）中估算的土壤热参数，假设250MVA线路承载了200A的负载电流，计算可得500MVA线路的持续运行载流量约为1030A，该值为标称额定电流值1255A的82%。可以看出，500MVA线路的降额运行是必需的，降额的大小取决于250MVA线路的实际负载电流。

2）紧急过负荷载流量

紧急过负荷载流量是指电缆在特定的持续时间内能运行的最大过载电流，此时电缆导体温度不超过容许值90℃，紧急过负荷载流量值取决于已加载电流的时间和线路可能承受过载的持续时间。图7所示为在72h末，500MVA线路突然承受1506A电流，相当于120%标称额定电流，与此同时，250MVA线路的负载电流为恒定的320A。从图中可知在过载运行45.5h之后，电缆导体温度达到90℃。进一步计算，当72h末过负荷分别为150%和180%时，持续运行时间分别为11.7h和4.7h。

图7 500MVA线路在120%过负荷条件下的计算导体温度

4 载流量的恢复

在特定的现场环境下，通过调查电缆的空间距离、埋设深度、地形以及土壤热阻率等因素，总结出形成热点的主要因素如下。

1）电缆交叉。

2）3根或更多电缆平行敷设。

3）电缆敷设在公路立交桥下方，使得雨水不能够浸润土壤。

4）电缆敷设在混凝土路面下方。

5）电缆被包裹在金属密闭空间结构中。

6）地下电缆埋设较深。

7）电缆轴向空间距离不充分。

为恢复整条电缆线路的载流量，本文采用一种通过移除电缆沿线热点顶部填土的方法，利用有限元软件“ANSYS”对该方法进行三维仿真分析。

为了简化仿真过程，假设只有一条230kV/500MVA的电缆线路埋在地下，所要缓和的热点位于坐标中心“O”。电缆及其周围土壤的稳态温度分布可以通过建立三维热模型求得。由于计算场域关于YZ平面对称，因此只建立一半区域的模型。

为了计算电缆的稳态温度分布，仿真时需对计算场域施加3种边界条件。

深层土壤温度恒定，三维模型的底面为第一类边界条件

三维模型的侧面水平温度梯度为0，因此，待研究场域侧面法方向的热流密度q可以写成

模型的顶部，也就是邻近空气的表面，这些面的法方向的热流密度q可以写成

式中，h为对流换热系数，单位为 W/m2/K；Tair为空气温度，单位为K。

第一类和第二类边界条件的选择对于温度分布有较大的影响，改变边界到中心“O”点的距离，当距离大于10m以后，再次曾加边界的距离对稳态温度分布影响非常小。因此，建立宽度为10m，高度为10m+H的半立方体模型，另外，模型在Z方向的长度取 20m，使得沿 Z轴距离热点“O”较远的地方温度能够达到稳定。通过从已建立的半立方体模型中心“O”正上方减去一个深1.2m，宽1m，长度为3m的半立方体区域来模拟本文所提出的缓和方法。电缆的结构参数和敷设参数分别见表1和表2。

表2 230kV充油电缆的敷设参数

假设电缆承载了1255A的标称额定电流，利用计算得到的相关区域的损耗值以及敷设参数值，电缆及其周围区域的稳态温度场如图8所示。

图8 稳态温度分布图

图9为沿Z轴从-10m到10m导体的温度曲线。可以看出，随着到中心点“O”（热点）距离的增加，电缆导体的温度逐渐增加，最后保持稳定在73.6℃。与距离较远处的温度相比较，处于中心位置“O”点的热点温度减小到 64.7℃。这个显著地温度下降证明了本文所提出的方法能有效的缓和热点的影响，从而恢复整条电缆线路的载流量。本文的研究是从热点“O”的上方移除一个深1.2m，宽2m，长3m的立方体区域，显而易见的，热点的温度降以及电缆载流量恢复的程度和所移除的土壤区域的体积有关。移除较多的土壤有助于加强热点上方的对流换热过程，在实施过程中，移除土壤区域的大小取决于现场条件。

图9 沿Z轴从-10m到10m导体的温度曲线

5 结论

本文提出一种有限元数值计算方法与基于梯度的优化方法的组合方法，基于DTS测量的电缆表面温度曲线，识别和定位电缆沿线的温度最高点，并且利用该方法估算出土壤的热参数进而实现电缆载流量的实时评估。以实际应用的一条230kV/500MVA电缆线路为例，对其长期运行额定载流量及紧急过负荷载流量进行了精确的评估，证明了该方法的正确性和有效性。

为了缓和热点温度并且恢复整条线路的载流量，本文采用一种通过移除电缆沿线热点顶部填土的方法，利用大型通用有限元仿真软件对这种方法进行三维仿真分析，结果表明热点有显著的温度下降，能够有效地恢复电缆的载流量。

[1] IEC 60287-1, Calculation of the Current Rating-Part 1:Current Rating Equations(100%Load Factor)and Calculation of Losses[S]. 2001.

[2]IEC 60287-2, Calculation of the Current Rating-Part 2:Thermal Resistance[S]. 2001.

[3]IEC 60287-3, Calculation of the Current Rating-Part 3:Sections on Operating Conditions[S]. 1999.

[4]曹惠玲,王增强,李雯靖,等.坐标组合法对直埋电缆与土壤界面温度场的数值计算[J].电工技术学报,2003, 18(3): 59-63.

[5]王有元,陈仁刚,陈伟根,等.基于有限元法的XLPE电缆载流量计算及其影响因素分析[J].重庆大学学报, 2010, 33(5): 72-77.

[6]孟凡凤,张兵,方晓明,等.影响直埋电缆载流量的因素的研究[J].绝缘材料, 2007, 40(3): 64-66.

[7]郑雁翎,许志亮,张冠军,等.采用Matlab仿真的变电站高压进线温度场和载流量数值计算[J].高电压技术, 2012, 38(3): 566-572.

[8]李伟,曾宏,杨琳,等.单芯电缆实时载流量计算方法研究[J].四川电力技术, 2011, 34(4): 61-64.

[9]YOON K T, TEO D S A. Controlling and monitoring Singapore's underground grid[J].IEEE Computer Applications in Power, 1999, 12(4): 23-29.

[10] NEHER J H. The transient temperature rise of buried cable systems[J].IEEE Transactions on Power Apparatus and Systems, 1964, 83(2): 102-114.

[11]凌永祥,陈明逵.计算方法教程[M].西安:西安交通大学出版社, 2005.

[12]孔祥谦.有限单元法在传热学中的应用[M].北京:科学出版社, 1998.