基于双环形旋涡相位调制的多焦点产生＊

谭志华，翁晓羽，隋国荣，郭汉明

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

随着物镜数值孔径的提高，光波的矢量特性对焦点区域光强分布影响越来越大。为此，标量衍射理论对研究高数值孔径物镜的聚焦问题将不在适用。Wolf等人基于Debye矢量衍射理论研究了线偏振光经高数值孔径聚焦之后的焦点区域光强分布，发现其光斑形状成椭圆形［1］。对于非均匀偏振的矢量光束，即柱矢量光束，其聚焦特性更加引人关注。如径向偏振光经高数值孔径聚焦之后产生比线偏振光更小的圆对称光斑［2］，而且其光场主要是由光场的轴向分量组成［3］；方位偏振光聚焦之后则会产生中空环形光斑［3］，若在物镜前面放置拓扑数为1的旋涡相位板对其波前进行调制，则在焦点区域内产生尺寸可突破光学衍射极限的光斑，而且其光场由横向分量组成［4］。这些特殊性质在光学显微成像［5］、光存储［6］、微粒控制［7］、电子加速［8］、光刻成像等领域都有着重要的应用前景。对于这种特殊的矢量光束，可以通过偏振膜来实现，而且可任意调节其偏振态［9］。

对微粒控制而言，当微粒的折射率大于周围环境的折射率时，光梯度力指向光强增大的方面，即微粒将会束缚在亮斑中心。所以在研究中除了要得到尺寸小光斑之外，还应在焦点区域上产生多焦点，以提高微粒捕捉的效率。通过多环带二元光学器件对入射矢量光束进行波前振幅调制在焦点区域产生沿光轴方向双焦点分布［10］。更为典型的方法是通过双环带复合光瞳滤波器对入射光波前相位及振幅进行调制，可在沿着光轴产生链状的光斑分布，即光链，调节两个环带的相位差可以控制光斑沿光轴连续移动［11］。在焦平面上，通过调节复合矢量光束各个参数可以产生4个圆形对称光斑［12］，而且其光强分布主要以光场轴向分量为主。上述产生多焦点的方法，都是通过波前振幅进行调制得到的，这不利于光能的充分利用。

本文通过设计双环形旋涡相位板对入射拉盖尔高斯柱矢量光束进行波前相位调制，以此在焦平面上产生多焦点。而且焦点数目可以通过调节旋涡相位拓扑数进行控制。与采用复合光束产生多焦点所不同的是，利用相位调制，可以在不损失光能的情况下产生多个焦点，而且可以得到光场由横向分量构成的焦点及主要由轴向分量组成的多焦点。多焦点的出现可以提高微粒捕捉效率，这种方法可以应用到折射率高于环境折射率的微粒捕捉上。

1 基本理论

一束柱矢量光波沿z轴正方向传播，若没有经过双环形旋涡相位板对其波前相位进行调制，在如图1所示的消球差成像系统（像方为空气）聚焦，像空间中任意点P（ρs，φs，zs）在柱坐标系下的电场分布为［3］：E（ρs，φs，zs）＝Exex＋Eyey＋Ezez（1）其中，ex，ey，ez分别是x、y、z轴的单位矢量。图2所示为双环形旋涡相位板，其内环与外环的透过率分别为exp（i m1φ）和exp（i m2φ），r、R分别为双环形旋涡相位板的内外环半径。入射柱矢量光束经过双环形旋涡相位板进行调制后，由物镜聚焦，其焦点区域电场分布由内环及外环两部分光束聚焦电场叠加而成。根据矢量衍射理论，内环及外环光束聚焦电场表示为：

图1 聚焦原理图Fig.1 Schematic diagram of the optical system

图2 双环形旋涡相位板Fig.2 Double ring shape vortex phase plate

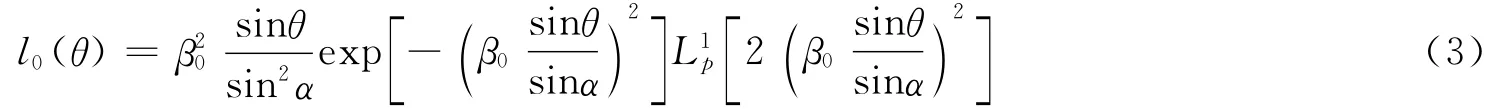
式中β0为入瞳半径与光束束腰之比为广义拉盖尔多项式。

对于入射光波为柱矢量光束，则V（θ，φ）为：

其中，φ0为柱矢量光束偏振方向与径向的夹角。由式（1）～（4）可以得到，焦点区域任意点P（ρs，φs，zs）的电场分布由内外环光束聚焦电场相叠加，即可表示为：

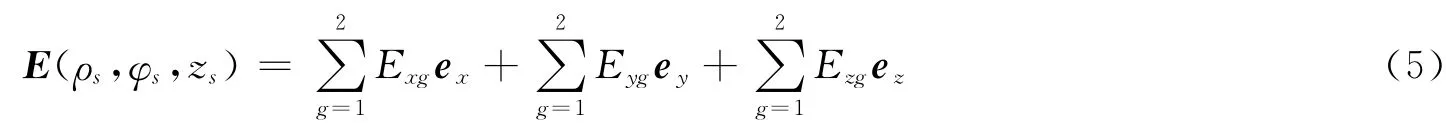
由式（5），可以得到光束经过双环形旋涡相位板调制之后的焦点区域光强分布为：

2 模拟计算与讨论

根据式（6），拉盖尔柱矢量光束经过双环形旋涡相位板调制后在焦点区域形成的光强分布可通过MATLAB编程进行模拟计算。取NA＝0.95，β0＝1.5，当φ0＝0时，通过调节内环半径r及内外环旋涡相位拓扑数m1、m2，可在焦点区域上产生多个光斑。

一般地，当φ0＝0时，即入射光为径向偏振光，在没有经过任何调制时，其焦点区域产生一个由光场轴向分量为主的光斑，而且其光斑尺寸比在相同条件下聚焦的线偏振光所形成的焦点更小。然而，经过本文所设计的双环形旋涡相位板之后，在物镜焦点附近产生多个光斑。图3为入射光波为二阶拉盖尔高斯光（N＝2），经不同内外环拓扑数和相同内环半径（即x＝0.8）的双环形旋涡相位板调制后焦点区域光强分布，图3（a）、（d）、（g）和（j）为光强的横向分量，图3（b）、（e）、（h）和（k）为光强的轴向分量，图3（c）、（f）、（i）和（l）为总光强分布。当m1＝1，m2＝－1时，在焦平面上产生双焦点（图3（c））；当m1＝2，m2＝－1时，产生三个焦点（图3（f））；当m1＝2，m2＝－2时，产生四个焦点（图3（i））；当m1＝2，m2＝－3时，产生五个焦点（图3（l））；可以发现，焦点数量取决于内外环旋涡相位的拓扑数，即等于内外环旋涡相位拓扑数绝对值之和。从能量分布的角度上看，焦点区域光强分布与一般径向偏振光（即没有经过波前调制）的光场分布类似，都是主要由光场的轴向分量组成。而且，光场横向分量随着内外环拓扑数的增大而逐渐远离光场轴向分量。此时，光斑由光场轴向分量构成。如图3（j）、（k）和（l）所示，焦平面上所形成的五个焦点由光场的轴向分量组成，而横向分量分散在外面。在微粒控制方面，多焦点的产生有利于提高微粒控制效率，达到一次可同时控制多个微粒。此外，光场由轴向分量组成可以大大提高光梯度力，有利于微粒的稳定捕捉。在光刻方面，若采用只对光场轴向分量敏感的材料，可以进一步减小光场横向分量的影响，实现多焦点光刻。

图3 N＝2，φ0＝0时，多焦点光强分布Fig.3 Multi－focal spots with N＝2，φ0＝0

图4是φ0＝π／2时，即入射光为二阶拉盖尔高斯方位偏振光（N＝2），经双环形旋涡相位板波前相位调制后的焦点区域光强分布。由于方位偏振光聚焦之后不存在光场轴向分量，焦点区域光场仅由横向分量组成。当m1＝2，m2＝－2，x＝0.75时，在焦平面上出现四个光斑（图4（a））；当m1＝2，m2＝－3，x＝0.69时，在焦平面上出现五个光斑（图4（b））；当m1＝2，m2＝－4，x＝0.8时，在焦平面上出现六个光斑（图4（c））；虽然x不同，但光斑数量还是取决于m1和m2的绝对值之和。多焦点的出现不仅可以提高微粒控制的效率，而且光场由横向分量构成，这有利于捕捉只对横向分量敏感的微粒。

图4 N＝2，φ0＝0.5时，多焦点光强分布Fig.4 Multi－focal spots with N＝2，φ0＝0.5

3 结 论

本文研究了在高数值孔径物镜聚焦下的拉盖尔高斯柱矢量光束经双环形旋涡相位板调制后的焦点区域光强分布。当入射光偏振态为径向偏振光，即φ0＝0，通过调节双环形旋涡相位板的内外环旋涡相位拓扑数及内环半径与孔径之比x＝0.8时，在焦平面上产生多个焦点，而且每一个焦点光强分布主要是由轴向分量组成。当入射光为方位偏振光时，即φ0＝0.5，通过改变双环形相位拓扑数，在焦平面上产生以纯横向分量组成的多焦点。焦平面上焦点数量取决于双环形旋涡相位板内外环拓扑数，即为内外环拓扑数绝对值之和。多焦点的出现，不仅可以提高微粒控制的效率，做到一次可控制多个微粒，而且在光刻方面，若采用只对轴向分量敏感材料，可以减小φ0＝0时光强横向分量的影响，做到多焦点并行光刻。这种产生多焦点的方法在微粒的控制及光刻方面都有着重要的应用价值。

［1］RICHARDS B，WOLF E.Electromagnetic diffraction in optical systems II.Structure of the image field in an aplanatic system［J］.Proc Roy Soc A，1959，253（1274）：358－379.

［2］DORN R，QUABIS S，LEUCHS G.Sharper focus for a radially polarized light beam［J］.Physical Review Letters，2003，91（23）：233901－1－233901－4.

［3］YOUNGWORTH K S，BROWN T G.Focusing of high numerical aperture cylindrical－vector beams［J］.Optics Express，2000，7（2）：77－87.

［4］HAO X，KUANG C F，WANG T T，et al.Phase encoding for sharper focus of the azimuthally polarized beam［J］.Optics Letters，2010，35（23）：3928－3930.

［5］SERRELS K A，RAMSAY E，WARBURTON R J，et al.Nanoscale optical microscopy in the vectorial focusing regime［J］.Nature Photonics，2008，2：311－314.

［6］KIM W C，PARK N C.Investigation of near－field imaging characteristics of radial polarization for application to optical data storage［J］.Optical Review，2007，14（4）：236－242.

［7］SHIMIZU Y，SASADA H.Novel optical trap of atoms with a doughnut beam［J］.Physical Review Letters，1997，78（25）：4713－4716.

［8］HAFIZI B，ESAREY E，SPRANGLE P.Laser－driver acceleration with Bessel beams［J］.Physical Review E，1997，55（3）：3539－3545.

［9］满忠胜，郭汉明，董祥美.基于圆锥偏振装置的非相干柱对称偏振光束产生方法［J］.光学仪器，2011，33（4）：37－41.

［10］XU Q，CHEN J.The creation of double tight focus by a concentric multi－belt pure phase filter［J］.Optics Communication，2012，285（7）：1642－1645.

［11］ZHAN Y，ZHAN Q.ZHANG Y，et al.Creation of a three－dimensional optical chain for controllable particle delivery［J］.Optics Letters，2005，30（8）：848－850.

［12］GUO H，SUI G，WENG X，et al.Control of the multifocal properties of composite vector beams in tightly focusing systems［J］.Optics Express，2011，19（24）：24067－24077.

［13］KOZAWA Y，SATO S.Focusing property of a double－ring－shaped radially polarized beam［J］.Optics Letters，2006，31（6）：820－822.