基于范成原理的渐开线圆柱齿轮参数化设计

郭海鹏

(陕西恒鑫精密纺织机械有限公司，陕西 宝鸡 721013)

渐开线圆柱齿轮是机械传动中应用最为广泛的齿轮机构，以往我们都是依据标准或者设计手册进行齿轮的设计，计算出齿轮工作图上的各个参数和尺寸。但是随着科学技术的发展，对齿轮机构的寿命、噪声提出了更高的要求。同时为了发展体积小重量轻的传动机构，需要尽可能的通过精确的计算和分析进行齿轮的设计。为此，我们首先要从齿轮的几何学入手建立准确的齿轮模型，再进行齿轮的受力分析。

1 范成齿形的基本原理

1.1 渐开线圆柱齿轮齿面形成的几何原理

渐开线圆柱齿轮(以下称齿轮)齿面是渐开线螺旋面，其形成原理如图1所示。在一直径为rb的基圆柱面上放一块长方形平板，在平板上画一条与基圆柱轴线成βb角的直线KK，当平板沿基圆柱体作纯滚动时，直线KK上的每一点都画出一条渐开线，由这些渐开线所形成的螺旋面即是斜齿轮的齿面，这些渐开线的起点是直线KK与基圆柱面的依次接触点，由这些接触点在基圆柱面上所形成的是一条螺旋线AA。

图1 渐开线圆柱齿轮齿廓形成原理

1.2 齿轮的范成法齿形加工原理

齿轮的滚齿过程是将齿坯与滚刀成一定角度安装，利用范成法原理滚切而成。我们可以理解成齿轮与齿条的啮合过程，齿条的法截面齿形即是滚刀齿形，滚刀齿形参数选用标准植。为保证正确啮合，齿轮端面齿形与齿条端面齿形的模数mt和压力角αt应该相同，且齿轮的分度圆螺旋角与齿条的倾角应该相同。

1.3 圆柱齿轮传动设计的相关参数

设计齿轮时已知齿轮齿数z，法面模数mn，法面压力角αn，法面变位系数χn，分度圆螺旋角β，法面齿顶高系数h*an，当法面模数mn≥1时法面顶隙系数c*n=0.25当mn＜1时法面顶隙系数c*n=0.35，刀具法面齿顶圆角ρ。

(9)不根切的最小变位系数χmin

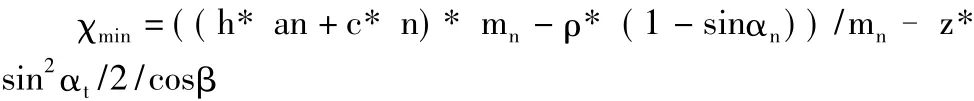
2 渐开线和过渡线的方程推导

标准渐开线圆柱齿轮单侧齿廓由4段曲线组成，即齿顶圆部分、渐开线部分、过渡线部分和齿根圆部分。齿顶圆部分由齿轮毛坯外圆直接车制，齿跟圆由刀具齿顶包络而成，齿顶圆和齿根圆直径可根据上面的公式计算。下面推导渐开线和过渡线的方程。

2.1 渐开线方程的推导

设范成加工时刀具与齿坯的初始位置如图2所示，齿轮基圆齿槽半角ηb可按下式计算：

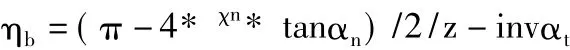
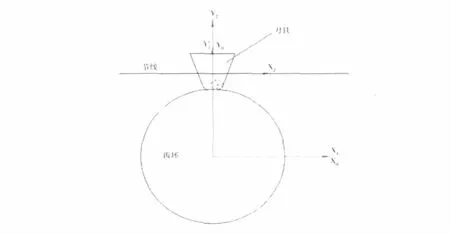
图2 范成加工时刀具与齿坯的位置

渐开线方程为：

2.2 过渡线方程推导

过渡线由刀具齿顶圆角(顶点)在齿坯上范成滚切时包络而成。

当刀具与齿坯位置如图2所示时，建立支架固定坐标系S0(O0X0Y0)、齿坯动坐标系S1(O1X1Y1)，此时S0与S1重合。

当刀具与齿坯啮合转动至图3所示时，建立刀具动坐标系S2(O2X2Y2)，此时S1相对 S0旋转角度φ，记作S'1。此时，刀具圆角与齿坯齿廓过渡线的共轭法线方向通过固定坐标系S0的Y0轴，设刀具从左向右运动，则齿坯过渡线刚开始形成。根据几何关系可求得

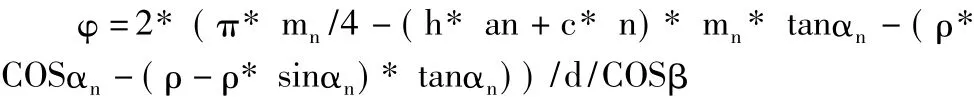
当刀具与齿坯啮合转动至图4所示时，刀具向右移动了L距离，根据Willis定理，此时刀具圆角与齿坯齿廓过渡线的共轭法线方向通过节点P。设共轭点在刀具动坐标系中的坐标为(X2，Y2)，根据几何关系可推导 L=X2*Y2*cos2β/(Y2+HF-ρ)-X2。此时，齿坯动坐标系相对S'1旋转θ角度，θ=2*L/d

坐标变换式分别为：

图3

因此，共轭点在齿坯动坐标系中的坐标可由刀具动坐标系变换而来，即

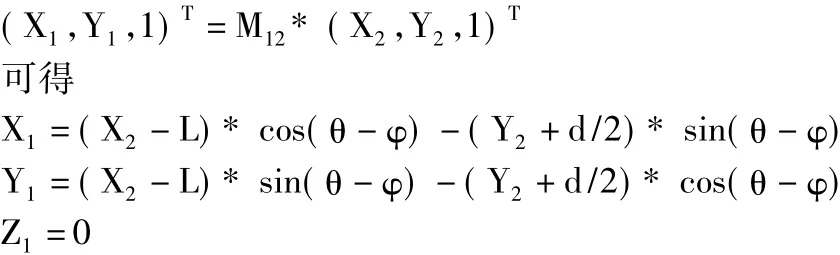
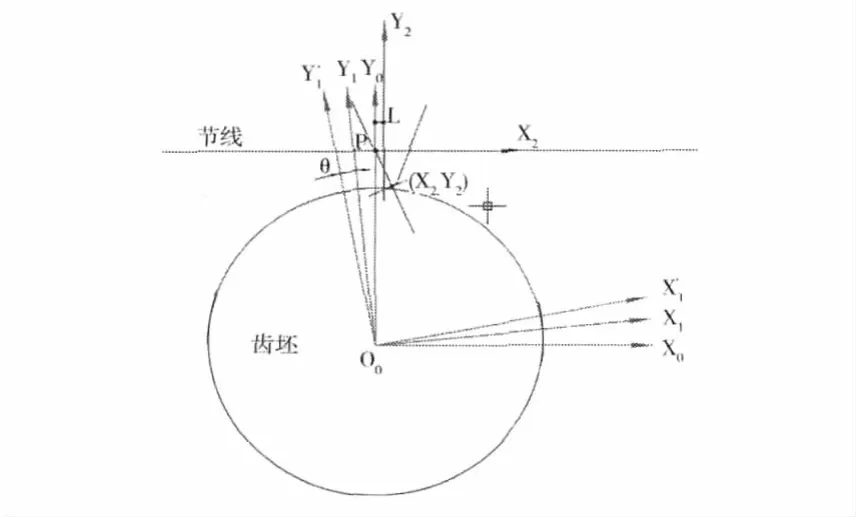
图4

3 渐开线圆柱齿轮的参数化设计过程及实现

3.1 渐开线圆柱齿轮的参数化设计过程

Pro/E是目前国际市场上最有影响的高级CAD/CAM工程软件之一，其最大特点和优势在于全参数化、全相关、基于特征的实体建模。本文利用Pro/E的【程序】功能进行齿轮参数的计算，通过创建方程曲线的方法绘制渐开线、过渡线和螺旋线，并利用Pro/E基于特征的实体建模方法和参数化功能进行渐开线圆柱齿轮的参数化设计，详细设计过程如下图5所示。

图5 渐开线圆柱齿轮的参数化设计过程

3.2 系统实现及实例

4 结论

本文通过合理地建立坐标系，提出了一种基于坐标变换推导齿根过渡曲线的方法，利用通用工程软件Pro/E里实现了渐开线圆柱齿轮的参数化设计。通过生成的模型可以直观的了解所设计的齿轮在实际范成加工后的状态，可以分析齿轮是否跟切或者齿顶变尖，从而在设计阶段排除不合理的设计。也可以通过这个精确的模型进行齿轮的受力和强度分析，将模型转入FEA工程分析软件通过划分网格，加载、后处理等实现CAD/CAE设计。遗憾的是，由于工程软件的计算方法和绘图精度的原因，实际绘制的方程曲线与理论曲线有一定的误差，在参数改变至某些值(如mn≤19)时，模型再生会产生失败特征。

［1］机械设计手册第五版机械传动卷［M］，成大先，化学工业出版社，2010.

［2］微分几何与齿轮啮合原理［M］，傅则绍，石油大学出版社，1999.

［3］齿轮几何学与应用理论［M］，F.L.李特文(Litvin)，上海科学技术出版社，2008.

［4］BS ISO 21771：2007，Gears—Cylindrical involute gears and gear pairs—Concepts and geometry［S］.

［5］Pro/E参数化高级应用教程［M］，黄恺，李雷，刘杰，化学工业出版社，2008.