巧构辅助函数证明微分中值定理

吕端良 王云丽

(山东科技大学 泰安校区，山东 泰安 271000)

高等数学中微分中值定理的证明方法比较多，本文受高等数学(同济五版)P132页第13题启发，通过构造一个三阶行列式辅助函数，应用Rolle微分中值定理，证明了Lagrangge微分中值定理和Cauchy微分中值定理。

定理 设函数f(x)、g(x)、h(x)在闭区间[a，b]上连续，在开区间(a，b)内可导，则在区间(a，b)内至少存在一点 ζ，使得

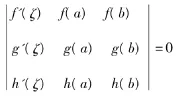
则有该函数在闭区间[a，b]上连续，在开区间(a，b)内可导，且根据行列式的性质得

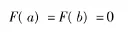
所以函数F(x)在区间[a，b]上满足Rolle微分中值定理的条件，故由Rolle微分中值定理知，在区间(a，b)内至少存在一点 ζ，使得 F'(ζ)=0

又根据行列式的性质及求导公式得F'(x)=

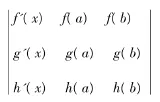
推论1.(Lagrange微分中值定理) 设函数f(x)在闭区间[a，b]上连续，在开区间(a，b)内可导，则在区间(a，b)内至少存在一点ζ使得

证明 构造辅助函数，在定理1证明中的辅助函数F(x)里，令g(x)=x、h(x)=1，该定理就得到了证明。

推论2.(Cauchy微分中值定理) 设函数f(x)、g(x)在闭区间[a，b]上连续，在开区间(a，b)内可导，则在区间(a，b)内至少存在一点ζ，使得

证明 构造辅助函数，在定理1证明中的辅助函数F(x)里，令h(x)=1，该定理就得到了证明。

[1]同济大学应用数学系.《高等数学》.高等教育出版社.2011.5