力学在机械工程中的延伸应用

司 建 崔立达

1中航工业河南新飞专用汽车有限公司（453000） 2新乡市高服筛分机械有限公司（453000）

机械工程设计应用中，我们会遇到各种各样的问题，如机械产品的系列化设计，在大小不同的型号设计中，我们如何把成熟产品的经验成功转移到其他系列产品中。显然，若机械地采用几何相似形状比例放大是不科学的,因为构件尺寸的改变，外部受力环境的变化，其构件的力学强度、刚度、形变、体积、振动频率等均发生了非比例的变化。再如在大型机械设备设计中，我们可以利用小型验证机形式来检验大型设备的合理性和可行性，那么小型验证机如何可靠地模拟出大型设备的机械特征，使实验真实的反映出可靠数据，实践证明力学模型是一个较为简便实用的方法，下面就此展开讨论。

1 固态线弹性体的相似模拟

首先我们把各式各样的承载件抽象称为满足虎克定律的固态物质构成的连续弹性体,可以假定，当作用于这一物体任一点外力为零时，其任一点的内应力也为零。

设这一受密度等于P1（X,Y,Z）的面积力和密度等于P2(X,Y,Z)的体积力，物体上一点由P1产生的应力、应变、变形分别为 б1、ε1、Y1，由 P2产生的应力、应变、变形分别是 б2、ε2、Y2。

取任一曲面S将物体分离并研究分离体必有下式成立:

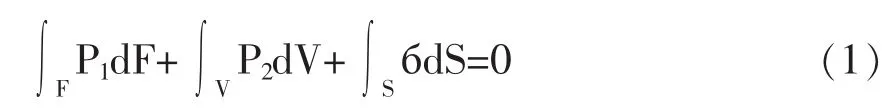
б是分离面上的应力，S是分离面面积，F是分离体外表面（不含S），V是分离体所处的空间。

1）如果面积力密度=P1×A,体积力密度=P2×B,则由线性系统的可迭加性知,应力=б1×A+б2×B,应变=ε1×A+ε2×B,变形=Y1×A+Y2×B。

2）当P2=0，面积力密度=P1，物体尺度变为C倍（即物体内任意两点的距离L均变为BL）时，相当于式1中每一面积均变为C2倍，即下式成立:

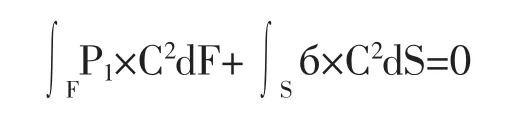
从而应力=б1，应变=ε1，因为变形=原始尺寸×应变，故变形=Y1×C。

3）当P1=0，体积力密度=P2，尺度变为C倍时有:

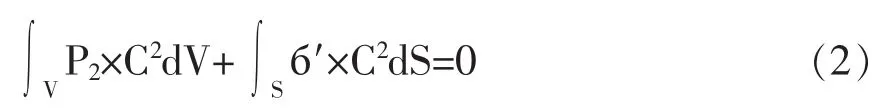
从而 б′=б2×C,即应变=ε2×C,变形=Y2×C″。

4）综上所述，当面积力密度=P1×A，体积力密度=P2×B, 尺度变为 C 倍时， 应力=б1×A+б2×B×C,应变=ε1×A+ε2×B×C,变形=（Y1×A+Y2×B×C）×C。

假设存在各种不同的应用环境，把不同的参数带入公式，可得出表1中一些有用的推论。

2 固态线弹性体自由振动的相似模拟

设线弹性体作简谐、稳态、同步的自由振动,即每点 i的位移均可表示为 Yi=ΣCij×COS(ω0j×t)，ω0j是第j阶固有圆频率(简称频率),我们仅考察其某一阶的固有振动。

弹性体内任一无穷小的分离体都在作相同频率、相同相位的振动。设它的外表面是曲面S,它包围的空间为V,在ω0j×t=Kπ时,分离体各点的位移即变形达最大值，振幅、加速度也达最大值，而速度=0。研究这一时刻的状态，使动力学问题形式上变成了仅受体积力和惯性力的静力学问题。

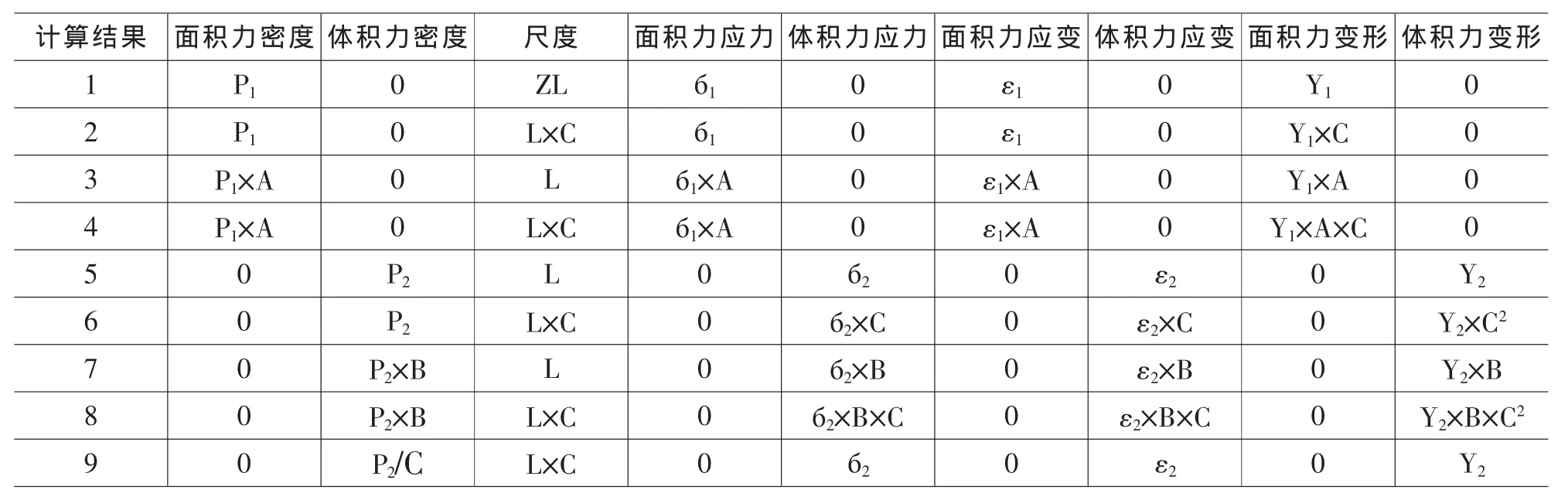
表1 固态线弹性体的相似模拟

设密度不变,物体尺度变为C倍,求固有频率ω0j`，设体积力密度不变,即最大振动加速度不变(这一假设并无必要,因为线性系统作自由振动时的振幅与频率无关，这里仅是为了叙述方便)，由表第6项计算结果得应力变为C倍,变形变为C2倍有下式成立:

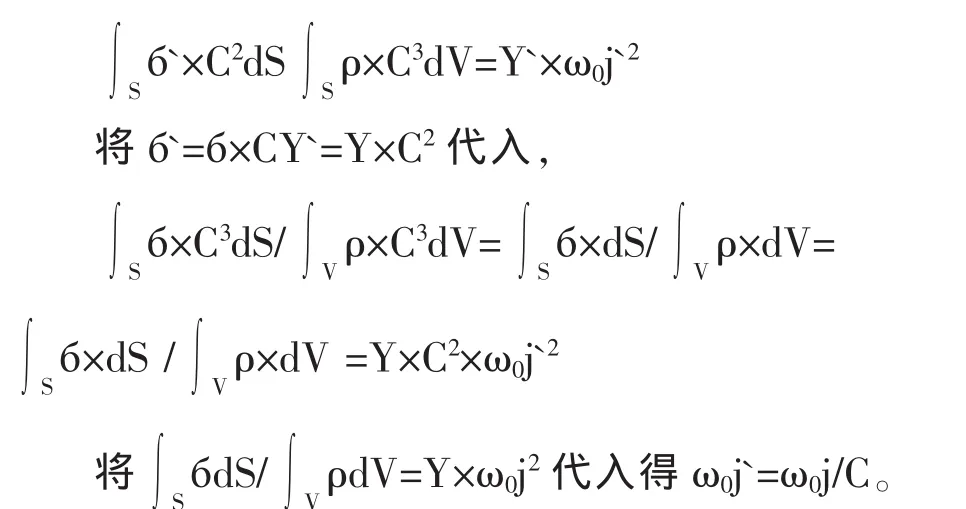
结论:线弹性体的固有频率与尺度成反比，或者说,线弹性体的固有振动周期与尺度成正比。

3 固态线弹性体强迫振动的相似模拟

现将振动器及振动体的尺度变为C倍,而将振动器的工作频率变为1/C倍，由于振动体的固有频率也变为1/C倍，故工作频率与固有频率之比W不变。

振动器的偏心块质量变为C3倍，偏心块的偏心矩变为C倍,从而振动器的偏心质量矩变为C4倍,振动力=质量矩×工作频率平方,故振动力变为C2倍。

振动器与振动体间的作用力及振动体各构件间的作用力视为面积力，因作用面积也变为C2倍，故面积力密度不变。但因为振动体的质量变为C3倍,而振动力变为C2倍，故惯性力密度变为1/C倍。根据表中计算结果9知应力不变，我们可以计算振动强度的变化，并以振动输送机械为例加以说明，振动强度=振动加速度/重力加速度。由于振动加速度变为1/C倍，故振动强度变为1/C倍，因此,上述方法虽然可以准确地模拟刚度和强度但不能模拟振动强度K。但对振动输送来说,模拟为相同的振动强度K是重要的，因为平均输送速度=A×φ(K)×g/ω，式中A是与槽体角度、振动方向有关的数,g为重力加速度,ω为工作频率，要使振动强度不变,需要振动力变为C3倍。这时可以采取如下方法:令工作频率=ω/C0.5,振动力变为C3倍,从而振动强度K不变，模型机的物料输送速度=真实机的物料输送速度×C0.5，由此可以计算真实机的产量。

上述计算对于减振弹簧同样适用，不过重力的影响用这一方法不能模拟，但因在振动机械中重力影响较小，所以,上述结论适用于重力可以忽略的场合。一般说来,我们是用小机器模拟大机器,即C＜1状况，若材料不变,可以精确模拟刚度，若模拟强度,还须考虑尺寸系数的影响。

4 以上论述的实际用途

1）静力模拟的应用

如果一机器或结构的构件自身重量和惯性力很小,甚至可以忽略,并且不存在导热等问题,那么就可以用此种方法设计。比如压力容器、起重工具、低速传动件、连接件等，也可以对满足上述条件的局部按上述方法设计,对其余部分另作考虑。

2）振动机械方面的应用

振动是很复杂的问题，有些问题没有好的算法,计算机模拟也有不足之处。另外，振动机械往往体积很大，实验风险和投入的成本都很高。有些机器长达数十米，重达数十吨，故做小模型机试验很合算。如果做1:10的模型,仅需1/1 000的材料消耗，实验时电能消耗也较少。如果模型存在问题,修改或重做都简单，另外,小机器也易控制操作，破坏性试验的成本也小。