IGBT模块功率循环疲劳寿命预测

姚二现，庄伟东，常海萍

（1.南京航空航天大学能源与动力学院 江苏 南京 210015；2.南京银茂微电子制造有限公司 江苏 南京 211200）

0 引言

IGBT功率模块的封装正朝着低成本、小尺寸、高性能以及高可靠性发展。丝键合工艺是最早发展起来的、用于芯片与外界互连的技术；由于采用丝键合工艺可以通过改变连接线弧的形状和距离，使多种器件能使用同一基板和外壳，现在仍在模块封装工艺中占绝对的统治地位。常用的键合线材料有金、铜和铝3种，由于成本优势，铝是普遍应用的键合线材料。

据统计，引线键合造成的失效占到半导体器件的失效的49%[1]，可见键合线的可靠性对整个模块的可靠性的影响是非常关键的。

对功率模块铝键合线可靠性，国内外目前的研究不多，Ramminger[2]等从引线键合工艺产生的机械应力的角度讨论了铝线的引脚跟断裂问题，分析了热膨胀系数失配对失效的影响，并从断裂力学的角度提出了应变能破坏准则来确定裂纹扩展方向。Koji Sasaki与 Naoko Iwasa[3]利用裂纹张开位移（COD）研究了二维状态下键合线的裂纹扩展寿命。

铝键合线功率循环寿命可根据疲劳破坏进程分为3个阶段：裂纹萌生、裂纹扩展和失稳剥离。由于铝键合线与芯片材料的热膨胀系数不同，IGBT芯片与键合线在工作过程中反复通断电，其温度反复变化，由于功率芯片硅材料与铝线之间的热膨胀系数的显著差异，造成温度变化时在键合界面出现交变的热应力，随着循环次数的增加，在键合面附近产生疲劳裂纹。裂纹一旦产生，模块热阻就将急剧地增加；结温升高，裂纹扩展速率加快，因此裂纹扩展和失稳剥离是个很短的过程，铝键合线功率循环寿命主要是裂纹萌生寿命。

本文根据模块结构，利用数值计算软件ANSYS构建了IGBT功率模块三维切片模型，计算了铝键合线在功率循环条件下的应力应变状态；并分别根据应变能法和Coffin-Manson法计算了其功率循环寿命。

1 分析模型

1.1 键合线结构

功率模块中的铝键合引线互连如图1所示，考虑到该结构具有一定的周期性与对称性，为缩短分析时间，提高分析效率，选取单根键合线建立四分之一切片模型，如图2所示。

计算时采取以下处理：

1）不考虑键合过程造成的残余应力应变；

2）各层材料完美结合，无相对滑移；

3）芯片均匀发热；

4）忽略硅胶散热；

5）不考虑硅胶对键合线的压力。

为了方便比较键合面不同位置的温度与应力应变，定义键合面的4个特征点如图3所示。

1.2 材料模型及参数

大部分材料在计算中做弹性材料处理，其参数见表1。

图2 键合线的1/4有限元模型

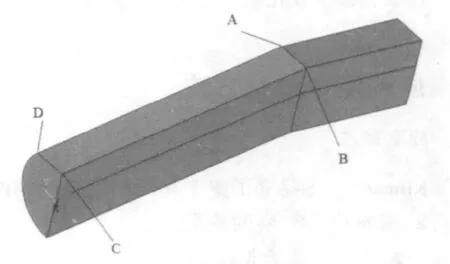
图3 键合面4点的定义

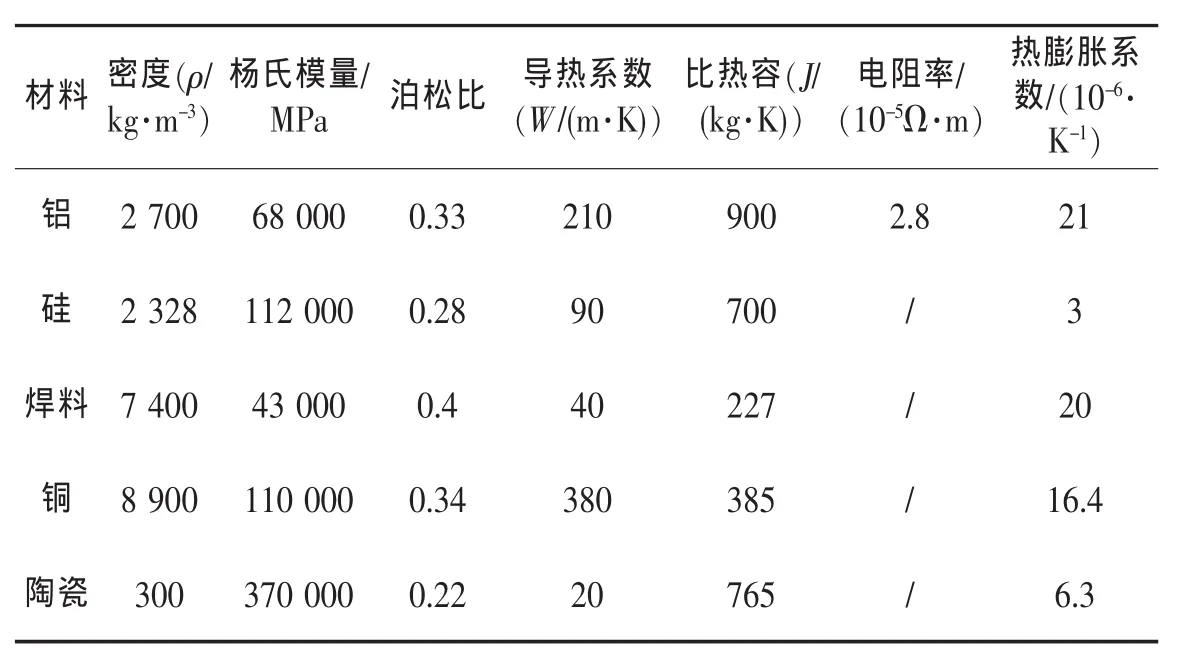
表1 材料特性表

本文在计算时将铝键合线作为双线性弹塑性材料，其屈服强度为30 MPa，切线模量为500 MPa。

1.3 网格与单元划分

简化后的模型有着简单的几何外形，划分结构化网格如图2所示。由于要进行耦合计算，在计算热电时单元类型采用Solid69，结构计算时用ETCHG命令将单元类型改为Solid45。

1.4 边界条件与载荷

功率循环采取方波加载，周期0.1 s，占空比为0.5，即升温与降温各占一半时间。

由于在功率循环过程中存在着热、电、应力等不同的物理场，所以在计算时需要考虑多场耦合，采用相应的算法进行计算。计算温度场的时候，采取直接耦合的算法，在铝键合线上施加恒定电流，在芯片上施加内热源。底面施加对流边界条件，其它面绝热。

结构计算时，采取间接耦合的算法，将热电计算得到的瞬态温度场作为载荷施加到模型上，将对称面设为对称边界条件，底面角点为固定约束，其它面自由。

本文分别计算了不同生热率下的模块应力应变，以获得温度变化幅度与功率循环疲劳寿命的关系。

2 疲劳寿命预测方法

2.1 应变能法

Kliman[4]等建立了单个循环的应变能密度增量△Wf与疲劳寿命Nf的关系：

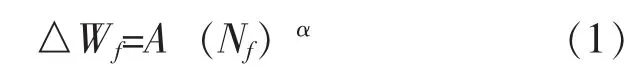
为便于由应变能密度得到疲劳寿命，可将上式改写为：

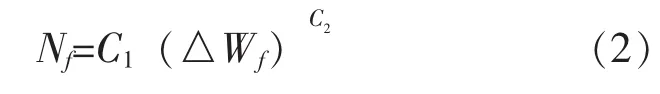
根据参考文献[5]的数据，拟合得到，C1=27，936，C2=-1.5。

用应变能法进行寿命预测时，首先运用ANSYS分析计算出在热循环过程中所积累的塑性应变能密度，然后再利用得到的应变能密度结合材料的单个循环的塑性应变能与疲劳寿命的关系来计算键合线裂纹萌生寿命。

在ANSYS后处理中，首先寻找塑性应变能密度最大的单元，然后根据不同的循环周期结束时的应变能密度数值，计算差值得到每周期应变能密度增量。将其代入公式（2），即可得到键合线的功率循环疲劳寿命。

2.2 应变法

1954年，Coffin和Manson在独立研究热疲劳问题的过程中分别提出了一种以塑性应变幅为参量的疲劳寿命描述方法[6]。他们发现，当利用塑性应变幅εp/2的对数与发生破坏的载荷反向次数2Nf的对数进行做图时，对于金属材料可以看到存在直线关系：

c——疲劳延性指数。

为了便于根据塑性应变幅来计算疲劳寿命，（3）式可转化为：

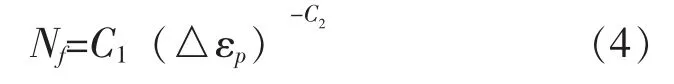
根据参考文献[7]，铝键合线的C1=16.55，C2=1.83。

在ANSYS后处理中，获取键合线不同时刻的塑性应变，计算得到塑性应变幅，代入公式（4）即可求得功率循环疲劳寿命。

3 计算结果与分析

3.1 温度与应力应变变化规律

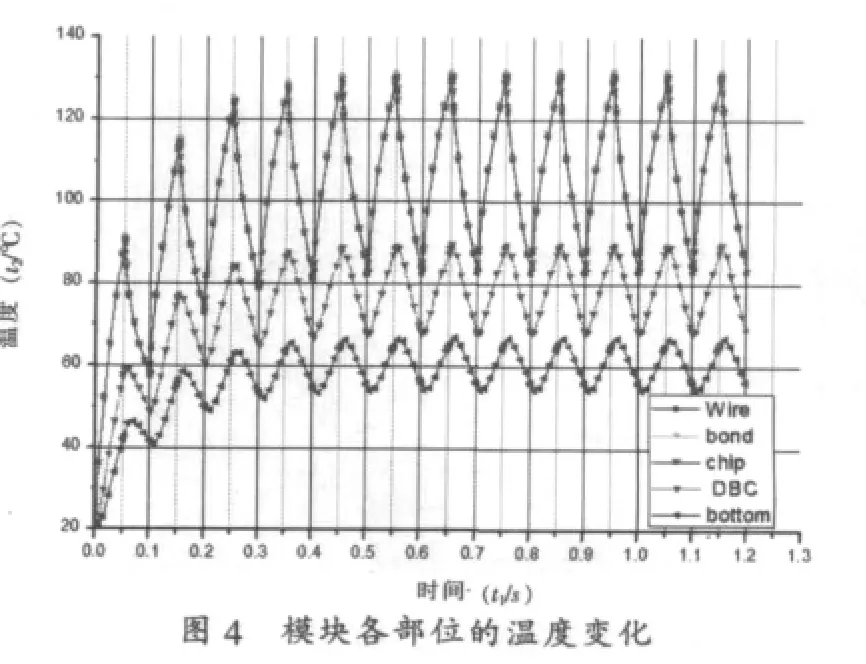
在占空比为0.5，生热率为20 W/mm3的载荷下，模型各部位的温度变化如图4所示，可以看出，5次功率循环之后，温度变化已趋于稳定；键合线，芯片温度变化幅度较大，DBC板的温度变化范围较小；还可以看出DBC中心与底部由于距离热源（芯片和键合线）较远，温度响应存在一定的滞后。

对比键合面4点的温度变化曲线（如图5所示），可以看出，键合面各点的温度几乎没有差别。

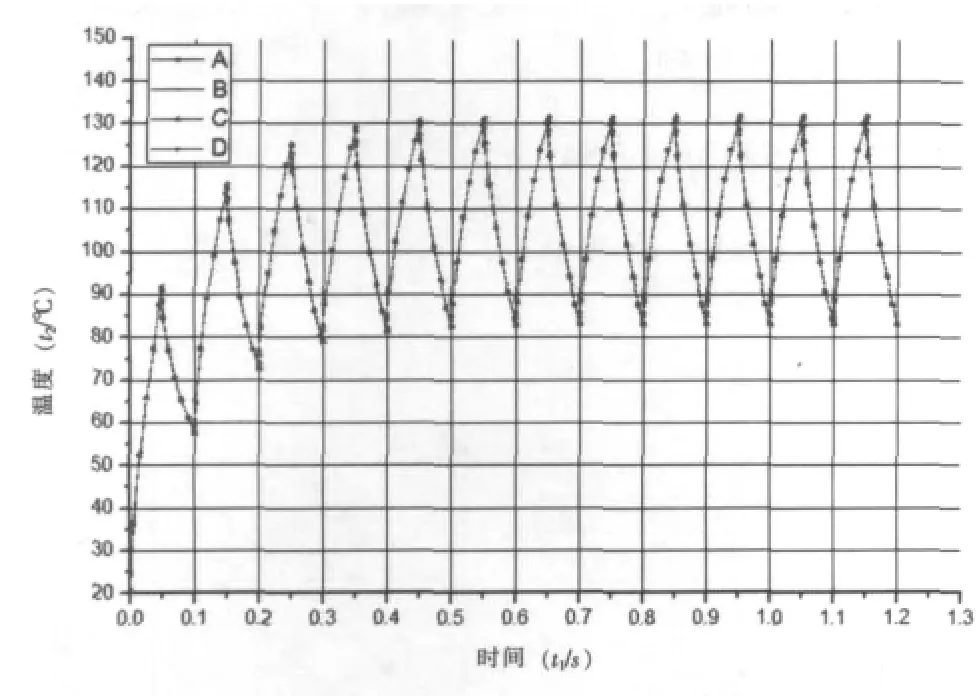
图5 键合面4点的温度变化

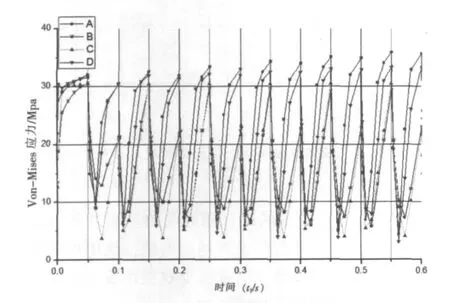
图6 键合面4点的应力动特性曲线

而从4点的Von-Mises应力变化曲线（如图6所示）可以看出各点应力水平存在很大的差别，Von-Mises应力最大值出现在A点，从键合界面外围往键合界面中心，应力幅值明显地降低。此结果符合键合物理模型的预期。

从等效塑性应变分布云图（如图7所示）可以看出，A点塑性应变最大，键合面上塑性应变分布同样从外围到中心逐渐地减小，可见键合线根部为疲劳危险区，这与实验中观察到键合线总是从根部开始剥离的现象一致。

图8是A点z向正应力随z向应变的迟滞曲线，从图中可以看出，随着功率循环次数的增多，迟滞曲线趋于稳定，说明每周期应变能增量趋于稳定。

图7 键合线等效塑性应变云图

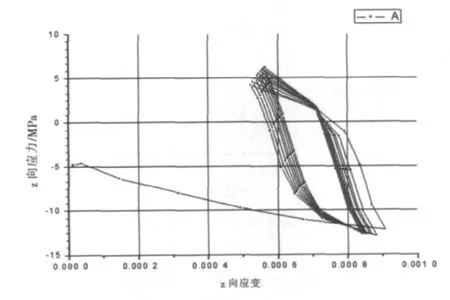
图8 A点z向应力-应变滞回环

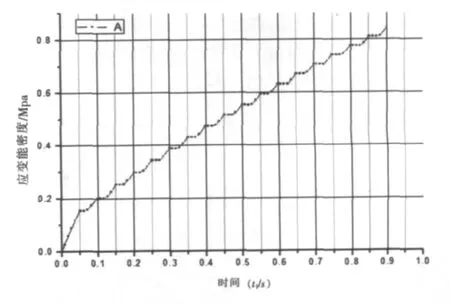
图9 A点的应变能密度动特性

图9为A点应变能密度动特性曲线，从中可以看出，应变能密度随时间增加近似阶梯状积累增加，在升温阶段及降温阶段前半段不变，后半段增加，说明材料发生了一定的塑性流动；经过9次功率循环后，每周期应变能密度增量已经趋于稳定，为0.06753 Mpa，代入公式（2），可以得出，在功率循环过程中，功率芯片结温的变化幅度为48.7℃时，其预计功率循环寿命为1592018次。

图10为A点等效塑性应变动特性曲线，从中可以看出，等效塑性应变随时间的增加近似阶梯状积累增加，其在一个周期内的变化规律与塑性应变能密度变化相似；随功率循环次数的增加，等效塑性应变的增幅在不断地减小，9个功率循环之后趋于一个稳定值，为0.00190，代入公式（4）可以得到在相同的循环条件下，塑性应变准则下其功率循环寿命为1572196次。

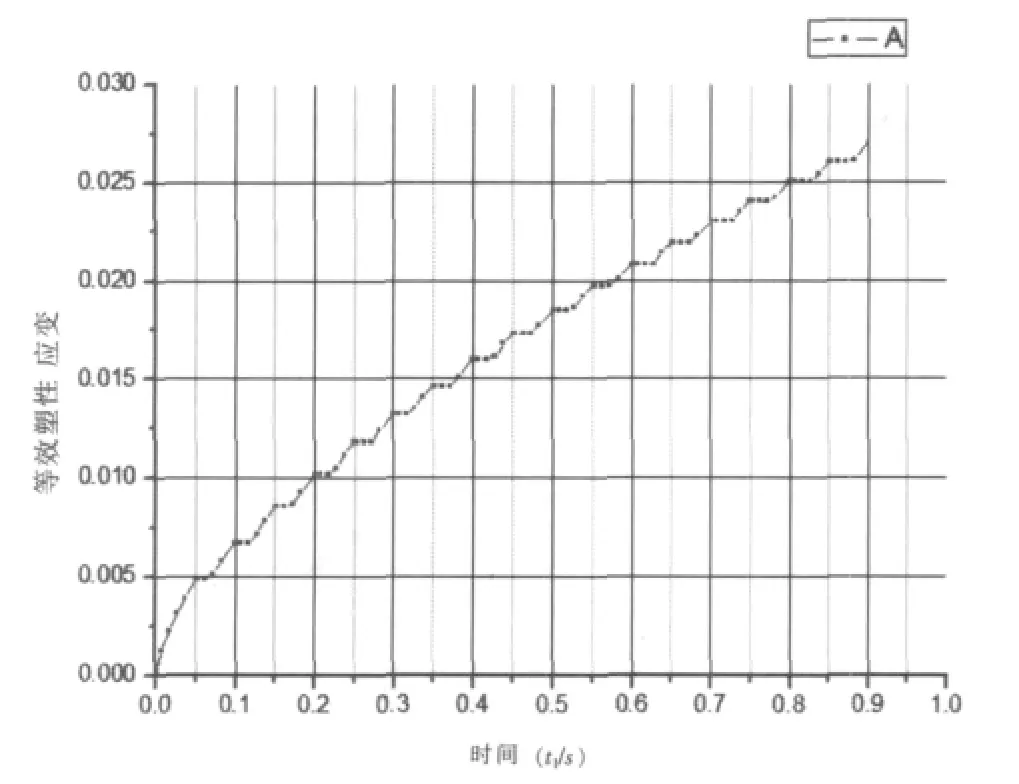
图10 A点等效塑性应变动特性

4.2 不同的温度波动幅度下模块功率循环寿命

为了获得键合面温度波动幅度对功率循环寿命的影响规律，本文计算了芯片生热率为15、17、22和25 W/mm3下的温度与应力应变，其它生热率下键合线的温度与应力应变变化规律与前文所述相同，只是数值有所差别。不同生热率下的温度变化幅度如图11所示：

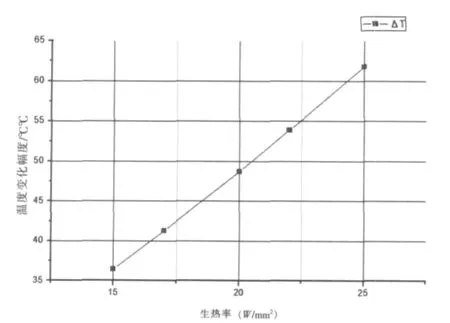
图11 不同生热率下的键合面温度波动幅度

从图11可以看出，由于生热率增加，单位周期内键合线与芯片发热量增加，键合面结温与温度波动幅度逐渐随之上升，波动幅度与生热率大致线性相关，拟合得到：

式（5）中：△Tj的单位为℃，生热率的单位为W/mm3。

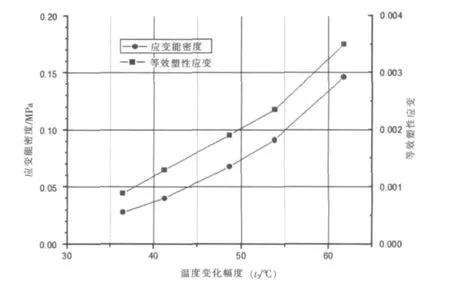
图12 不同温度波动幅度下应变能密度与等效塑性应变每周期增量

图12给出了不同键合面温度波动幅度下的应变能密度与等效塑性应变每周期增量，从中可以看出，每周期应变能密度增量，等效塑性应变增量均随温度变化幅度的增加而增加。

根据公式（2）与（4），计算并绘出不同温度波动幅度下应变能准则和等效塑性应变准则疲劳寿命如表2与图13所示。

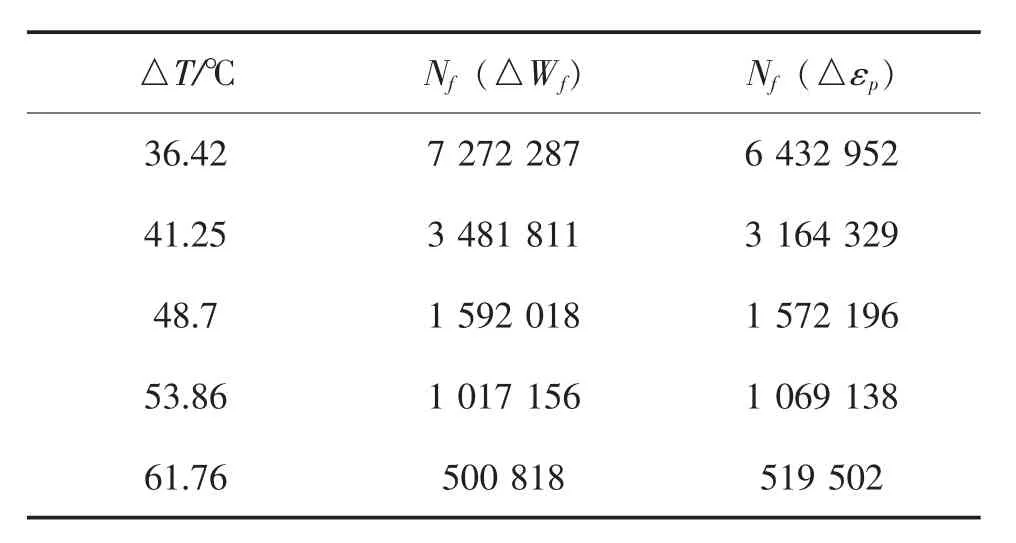
表2 不同温度变化幅度下两种疲劳准则寿命

由表3和图13可知，功率循环疲劳寿命在随键合面温度波动幅度的增加而急剧地减小，同时还可以看到，由两种准则得到的疲劳寿命是很接近的，对图13的两条曲线进行拟合，得到模块功率循环寿命和键合面温度波动幅度的关系为：

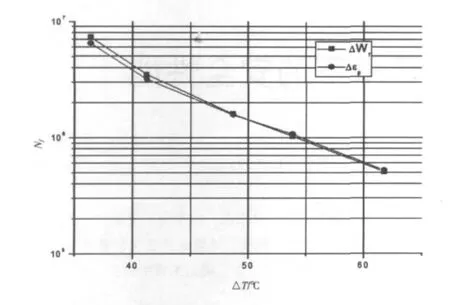
图13 不同温度变化幅度下两种疲劳寿命

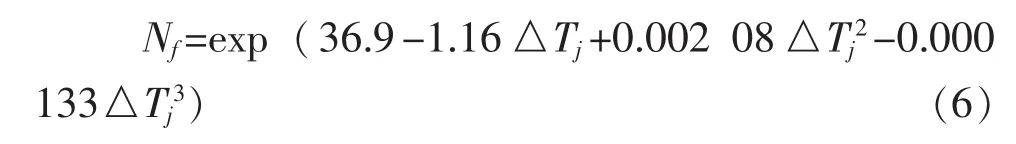
式（6）与两条曲线的误差在10%以内。

由于在较大的键合面结温幅度下，键合线的疲劳寿命较短，因此功率模块应避免极端的工作条件，并保持良好的散热。

5 结论

1）介绍了键合线功率循环失效的机理，材料热失配是造成键合线剥离的主要原因；

2）数值计算结果表明键合线根部的Von-Mises应力与等效塑性应变最大，是模块功率循环疲劳危险区，键合线剥离总是从根部开始；

3）应变能法和等效塑性应变法得到的功率循环疲劳寿命在数值上比较接近，这表明两者都是高效、准确的功率循环疲劳寿命数值模拟方法；

4）分析得到了芯片生热率、键合面温度波动幅度与键合线功率循环疲劳寿命的关系，对计算结果进行了拟合，得到了键合线功率循环寿命与键合面温度波动幅度的关系式；

5）模块功率循环疲劳寿命随结温变化幅度的增大而急剧地减小，因此功率模块在工作中应保持良好的散热，避免过大的热损耗。

[1]陈宇.集成电路封装用新型Al-1%Si键合线的研制[D].兰州：兰州理工大学，2004.

[2]RAMMINGER S，TUKES P，WACHUTKA G.Crack mechanism in wire bonding joints[J].Microelectronics Reliability.1998，38： 1301-1305.

[3]SASAKI K，IWASA N.Thermal and structural simulation techniques for estimating fatigue life of an IGBT Module.Proceedings of the 20th International Symposium on Power Semiconductor Devices&IC's[C]//Orlando，FL.2008：181-184.

[4]KLIMAN V.Fatigue life estimation under random loading using the energy criteria[J].Int J Fatigue，1985，（7）：39-44.

[5]LAZZARIN P，LIVIERIP，BERTO F，et al.Local strain energy density and fatigue strength of welded joints under uniaxial and multiaxial loading[J].Engineering Fracture Mechanics，2008，75： 1875-1889.

[6]雷东.疲劳寿命预测若干方法的研究[D].合肥：中国科学技术大学，2006.

[7]RAMMINGER S，SELIGERN，WACHUTKA G.Reliability model for Al wire bonds subjected to heel crack failures[J].2000，40： 1521-1525.