基于物理约束扰动的EnSRF雷达资料同化
闵锦忠,毕坤,2,陈耀登,王世璋
(1.气象灾害教育部重点实验室(南京信息工程大学),江苏南京210044;2.94608部队,江苏南京210022)
0 引言
当前数值预报已逐步成为现代天气预报技术的核心,随着模式的不断进步、计算能力进一步提升,模式分辨率也在向更高水平发展。尽管现代数值模式对天气过程发生发展的外部因素描述更加细致,但如何为高分辨率模式提供一个更准确的初值依然是一个极具挑战的问题。
就中尺度天气系统而言,多普勒天气雷达凭借其探测时空分辨率高的特点,成为监测预警的有效手段之一。如何将多普勒雷达探测结果有效融入数值预报模式中,提高灾害性天气的预测能力,前人已做了许多工作。Sun and Crook(1997,1998)应用四维变分资料同化方法(Four-dimensional variational data assimilation method,简称4D-Var)将雷达探测的径向风和反射率同化进云尺度数值模式;Gao et al.(1999)利用ARPS上构建的三维变分资料同化系统(Three-dimensional variational data assimilation system,简称3D-Var),同化了雷达径向风数据。尽管前期变分方案在同化雷达资料方面取得了一定成果,但就3D-Var而言,其使用的背景误差协方差在空间上是均匀且各向同性的,同时也不随时间改变;而对4D-Var来讲,其具有隐式的背景误差协方差调整特性,但在求解极小化过程中必须依赖伴随模式,困难之处不仅在于设计伴随,同时某些物理过程也不具备向后积分的特性。Evensen(1994)将集合预报与传统卡尔曼滤波器相集合,应用于高维数系统,形成了集合卡尔曼滤波器(Ensemble Kalman filter,EnKF)。EnKF可实现背景误差协方差随模式积分变化,同时不依赖伴随模式,可应用于复杂的非线性模式。
EnKF采用Monte Carlo方法来捕捉背景场不确定性,Evensen(2003)指出,不理想的初始扰动结构对EnKF的最终同化效果不会有太大的影响,但必须有合适的积分时间使得扰动发展。在风暴尺度EnKF研究中,Tong and Xue(2005)采取逐格点的Gauss随机扰动;之后Tong and Xue(2008)验证了经空间平滑后的Gauss随机扰动(全场随机扰动方案)在EnKF同化效果上要优于前期非平滑方案,表明研究的天气系统、同化间隔和扰动尺度之间具有密切联系。Zhang et al.(2009)和 Li et al.(2012)在对台风进行集合预报时使用3D-Var的CV3背景误差协方差创建扰动集合(简称RandomCV扰动;Barker et al.,2004;Barker,2005),本文将在第 2 节对此方案进行描述。但RandomCV扰动方案初始化的集合成员中小尺度信息不足,需要进行3~12 h的集合Spin-up以得到一个近似真实的中小尺度扰动分布。对近海台风而言,30~50个成员集合的Spin-up会耗费大量积分时间,这可能会错过预警的最佳时机,因此能否选择一种尺度更小且结构合理的初始扰动方案,在缩短集合Spin-up时间的基础上提高同化质量就具有重要的现实意义。
本研究完善了WRF集合均方根滤波同化系统(WRF Ensemble Square-Root Filter Data Assimilation System,WRF-EnSRF;闵锦忠等,2011)的双向嵌套预报方案,并融和了多微物理过程积分,同时将近几年发展的一种雷达资料质量控制方案加入系统。更为重要的是,为了在缩短集合Spin-up时间的基础上,同时能够提高同化的效果,引入一种具有物理结构且尺度可控的初始扰动方案,通过对比其与RandomCV扰动方案、全场随机扰动方案对超强台风“桑美”的雷达资料同化试验,考察新扰动方案的合理性和有效性。
1 WRF-EnSRF同化系统介绍
1.1 集合预报模式
研究采用基于WRFV3.3(ARW)版本构建的集合预报系统;预报区域采用两层双向嵌套方案,集合初始化分别在粗细两重网格中进行,并扰动侧边界;初始化集合成员采取Monte Carlo方法,但可选择3种结构差异较大的初始扰动方案(RandomCV、全场随机扰动和物理约束扰动);考虑模式误差,对模式微物理过程采取多方案集合的方法(Meng and Zhang,2007;Snook et al.,2011)。
1.2 EnSRF同化方案
传统的EnKF为防止观测误差被低估而引起滤波发散,一般要对观测进行加扰。由于EnKF采用集合样本估计背景误差协方差,之后再结合观测误差协方差更新集合成员,如对观测进行扰动势必会引入新的抽样误差,导致分析误差精度下降。为了避免上述情况发生,Whitaker and Hamill(2002)在Anderson(2001)的基础上设计了一个基于集合的均方根滤波的确定性算法。本研究采用这种观测不加扰的算法,同化系统与闵锦忠等(2011)一致。
1.3 雷达资料质量控制及观测算子
WRF-EnSRF系统对雷达探测的径向风和反射率资料进行直接同化,须将模式空间的物理要素经空间和物理变换计算到观测空间,关于径向风和反射率观测算子采用Tong and Xue(2005)的计算方法。
2 初始扰动方案及其设计
2.1 物理约束初始扰动方案的提出
在台风集合滤波同化研究中通常使用Random-CV方案,该方案采用GFS资料统计的背景误差协方差生成随机扰动,经垂直EOF、递归滤波和平衡方程约束后变换回模式空间,形成不同的成员,生成的背景误差具备空间相关性和物理关联性。但其主要反映大尺度系统的不确定性,而对中小尺度的协方差结构则必须经过空间插值,同时为弥补中小尺度的信息不足,还需3~12 h的集合Spin-up以发展合理的中小尺度扰动结构,若网格规模大、集合数多,集合Spin-up过程需耗费大量的积分时间。而在风暴尺度EnKF研究中,多使用逐格点或逐格点后平滑的Gauss随机扰动,其特点是尺度较小,但缺乏空间相关和物理约束,该方案加扰后并不需要较长时间的集合Spin-up,但要经若干次分析才能建立可信的相关关系(Tong and Xue,2005)。
由前面的描述可以看出,扰动尺度、空间相关结构和扰动变量的物理关系对缩短加扰后的集合Spin-up时间、加快建立正确的背景误差协方差具有重要的影响。本研究在此基础上,通过引入扰动势函数和流函数,建立一种尺度可控、部分满足约束方程的扰动方案(物理约束扰动方案)。该方案具体实施如下:首先在模式空间按一定均值、方差逐格点产生势函数和流函数的Gauss伪随机数;之后经空间递归滤波(Lorenc,1992;Gao et al.,2004),将扰动尺度调整到研究需要;最后按如下约束方程诊断出扰动的水平速度、垂直速度和位势高度。

式中:ψ'、χ'分别表示扰动流函数和势函数;V'h、V'3分别表示水平和三维风矢;φ'表示扰动位势高度;k为垂直方向单位矢。该式由原始方程中的水平运动方程和连续方程去掉倾向项得到,体现了速度场与质量场的平衡关系(Hollingsworth and Lonnberg,1986)。对具有复杂非线性结构的热力学变量和水汽变量,简单起见,直接使用递归滤波后的扰动场叠加到模式状态量上。

图1 不同初始扰动方案中扰动位势高度(阴影;单位:m2/s2)和风场(箭矢;单位:m/s)的比较 a.RandomCV;b.全场随机扰动;c.物理约束扰动Fig.1 Comparison of perturbed geopotential height(shadings;units:m2/s2)and wind field(vectors;units:m/s)in different initial perturbation schemes a.RandomCV;b.stochastic perturbation;c.physical constraint perturbation
2.2 扰动场对比分析
利用第2.1节描述的3种初始扰动方案各产生一个扰动场(标准差:水平风速3 m/s;扰动位温1 K;水汽混合比1 g/kg;扰动位势高度100 m2/s2)。图1给出了不同初始化方案在所示区域内模式层第8层(约850 hPa)的扰动位势场和风场。可以看出:由于RandomCV扰动方案使用的是插值后的协方差结构,扰动尺度明显偏大,所以需要较长Spin-up时间发展中小尺度扰动结构;尽管全场随机扰动的尺度较小,但位势场和风场的配置关系不好;而物理约束扰动使用的是扰动势函数和流函数,尽管生成方式与全场随机扰动类似,但经约束方程诊断为模式变量后,具有更小尺度的结构,同时扰动位势场和扰动风场具有一定的平衡关系。
3 同化数值试验
3.1 实况分析
2006年第8号台风“桑美”,于8月9日10时(世界时,下同)发展为超强台风,中心气压降至935 hPa,台风最大风速达到55 m/s,次日10时在浙江、福建交界处登陆,其间维持超强台风等级,中心最低气压为915 hPa,台风最大风速为60 m/s。台风登陆后强度迅速减弱,在浙闽沿海地区造成了很强的降水,其中心12 h累计降水超过200 mm。
3.2 同化试验方案
试验采取27 km(120 s)/9 km(40 s)、垂直28层的两重双向嵌套方案,使用分辨率为1°的NCEP/FNL分析资料和分辨率为20 km的JMA区域客观分析资料生成初始条件和边界条件,积云对流参数化方案为Kain-Fritcsh,行星边界层方案为YSU,确定性预报中的微物理方案使用WSM6,集合预报中微物理方案采取Lin和WSM6混合的方案。雷达资料选取温州站S波段多普勒天气雷达资料,经第1.3节中描述的质量控制算法进入同化系统。图2给出了WRF模拟区域和雷达探测范围。EnSRF同化参数:非水汽变量水平局地化半径100 km,垂直半径6 km;水汽变量水平局地化半径80 km,垂直半径16 km;松弛膨胀系数0.8;雷达径向风误差标准差2 m/s,反射率误差标准差2 dBz。
利用上面的模式设置,分别采用RandomCV方案、全场随机扰动方案和物理约束扰动方案进行集合初始化,扰动变量及扰动标准差与第2.2节中一致,在此基础上考察不同的初始扰动方案对EnSRF同化的影响。试验名称及方案设计详见表1。
调平控制系统Bode图如图5,相位裕度和幅值裕度均为正,该调平控制系统是稳定的。由Simulink仿真可得出控调平制系统单位阶跃响应曲线(图6),调平控制系统能达到稳定状态,但响应较慢,需设计模糊PID控制器。
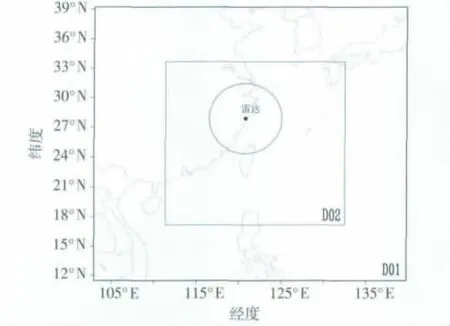
图2 模拟采用的两重嵌套区域示意图(黑圈:雷达扫描范围)Fig.2 Schematic diagram of two-way nesting regions in the simulation(black ring:radar’s covering)

表1 试验名称及方案设计Table 1 Experiment name and scheme design
模式在9日18时冷启动,积分6 h后进行集合初始化,形成30个集合成员。将集合成员平行积分3 h进入间隔30 min的分析循环,分析在10日06时终止,将得到的集合平均场匹配边界条件后一直预报到10日18时(图3)。
4 试验结果分析
4.1 同化结果分析
本文通过观测空间的“新息”平均、均方根误差和集合离散度评价同化效果(Aksoy et al.,2009),但计算“新息”均方根误差时与Aksoy et al.(2009)并不相同。这主要是因为在强天气过程模拟中,背景场与观测场的离差很大,“新息”平均经常出现强烈有偏的状况,若考虑该项会使得均方根误差产生虚假低值。因此,在观测误差允许的范围内,本文直接用“新息”向量的均方根评价同化前后模式空间诊断观测与真实观测的接近程度。
4.1.1 “新息”平均值
由分析前后观测空间的“新息”平均(图4)可以看出,不论采取哪种扰动方案,EnSRF分析会使得径向风(图4a)和反射率(图4b)的“新息”平均向0值靠近,这表明EnSRF分析具有类似“幂变换”的作用(Hamill,2001;Whitaker and Hamill,2002),对样本而言更接近Gauss形态。由于EnSRF同化理论是建立在Gauss假设基础上的,所以对于复杂非线性系统(数值模式和非线性观测算子)来说,该结论表明EnSRF分析后能够近似满足Gauss假定,这也是EnSRF适用于雷达资料同化的一个重要原因。对比3种方案的径向风“新息”平均(图4a)可知,全场随机扰动方案在分析循环前期比其他两种方案更合理,主要原因在于,“桑美”台风作为超强系统,其非水汽变量在模式中的线性属性较好,而具备物理结构的扰动方案会加大非线性效应的影响,分析后的集合预报具有较强非Gauss型分布。反射率的结果(图4b)与径向风的差异较大,模式中水汽变量具有较强的非线性属性,反射率与非水汽变量间相关性较差,同时雷达径向风同化贡献比反射率大很多,使得每次同化前反射率“新息”平均出现强烈的有偏性;但物理约束扰动的先验有偏性明显比其他两种方案小,表明该方案产生的集合成员能够较好地包含真值;同时由于需要剔除离差过大的观测,较小的先验“新息”平均也保证该方案可以更多地利用观测。由反射率的“新息”平均还可看出,在分析前期具备物理结构的两种初始扰动方案无偏性要比全场随机扰动好,同时“新息”平均收敛得更快,表明含有物理结构的扰动方案更好地表征了模式变量间的非线性相关。对比物理约束扰动和RandomCV扰动还发现,由于递归滤波器具有低通滤波的特性,经过3 h的集合Spin-up,较小的扰动尺度能够产生更为合理的中小尺度扰动结构。

图3 试验预报流程Fig.3 Flow chart of experiment forecasts

图4 径向风(a)和反射率(b)的“新息”平均Fig.4 Mean innovations of(a)radial velocity and(b)reflectivity
4.1.2 集合离散度水平
由于多普勒雷达探测的主要是对流区域,天气系统在该区域发生发展最不稳定,一旦含有中尺度信息的雷达资料进入模式,分析场就具备了更好的中尺度结构,因而能更有效地组织对流,在观测空间中的表象即离散度在分析循环中逐渐增加,最后增长率达到饱和。由图5可知,不论径向风还是反射率,不同的扰动方案在每次同化后离散度都非常接近,而在预报过程中却有不同的增长率,这也反映了同化雷达径向数据具有一定的“不适定”性,即便统计结论相差不大,其状态量的相空间也可能存在很大差异。离散度作为衡量集合成员差异的统计指标,其大小并不能直接反映同化效果的好坏,但过小的离散度会引起滤波发散致使滤波器过分忽略观测,但在该个例中,3种扰动方案的离散度在分析循环中基本都是增大的,离散度不足的现象并不明显。从不同的初始扰动方案看,物理约束扰动和全场随机扰动在分析循环前期的离散度较接近,但后期后者要明显大于前者,这主要是由于EnSRF方案更新的状态量在物理上是匹配的,而这种物理上的协调是有利于天气发展的,全场随机扰动的集合成员随着分析循环的进行会逐渐建立起合理的物理结构。对比RandomCV方案和物理约束扰动方案的径向风离散度(图5a)可见,初始扰动尺度较大的Ran-domCV方案离散度较小,随着分析循环的进行,离散度增长率会超过物理约束扰动。这说明EnSRF分析可以将集合扰动的尺度调整到一个合理的范围。对比反射率的离散度(图5b)可见,在分析后期具备物理结构的扰动方案离散度水平非常接近,但缺少物理结构的全场随机扰动则要大于其他两者;分析集合平均场发现,造成该现象的原因是由于该扰动方案下的成员组织的对流过强,产生很大一部分虚假回波。在整个分析循环过程中,相对其他两种初始扰动方案而言,物理约束扰动的先验离散度并未出现大幅增长;由于离散度是建立在集合平均基础上的,不稳定的集合平均往往会产生较大的离散度,显然RandomCV方案和全场随机扰动方案产生的这种增长与不合理的集合平均和扰动结构有关,而新方案避免了以上不足。

图5 径向风(a)和反射率(b)的离散度Fig.5 Spreads of(a)radial velocity and(b)reflectivity
4.1.3 “新息”均方根误差
图6给出了观测空间径向风和反射率相对于雷达观测的RMSE(其中对20~40 dBz和大于40 dBz的反射率分开统计)。由图6a可见,3种扰动方案均使得先验RMSE下降,这表明模式中台风的动力结构在向观测靠近,径向风的同化对台风预报起到了正的效果;就不同扰动方案而言,尽管每次分析后RMSE都很接近,但由于新方案能够较好捕捉不确定性的“流依赖”信息,更多利用反射率观测,所以其产生的先验RMSE明显比其他两种方案效果好;同时伴随分析循环的进行,具有物理结构的RandomCV方案也比缺乏物理结构的全场随机方案能获得更好的先验RMSE结果。反射率结果(图6b、c)与径向风类似,同化反射率资料使得RMSE随分析次数增加逐渐减小,但不同扰动方案的结果差异较大,由于RandomCV方案的随机扰动反映的扰动尺度较大,所以模式中水汽变量经3 h集合Spin-up发展得并不充分,造成第一次分析前反射率明显偏弱,而尺度较小的全场随机扰动和物理约束扰动在同化开始前能够获得更好的预报结果。

图6 径向风(a)、20~40 dBz反射率(b)和大于等于40 dBz反射率(c)的均方根误差Fig.6 RMSEs of(a)radial velocity,(b)20—40 dBz reflectivity,and(c)larger than 40 dBz reflectivity
4.2 预报结果分析
4.2.1 组合反射率、气压及风场
图7给出了同化末端组合反射率、海平面风场和海平面气压的比较。通过雷达径向数据的同化,基本可以反映台风的反射率结构;同时表明,EnSRF分析可以调整模式中水汽变量,缩短 Spin-up的时间。
对于图7b、c、d三幅图,在台风中心沿着虚线取剖面,以观察其绝对风速和位温的垂直结构(图8)。分析循环末端台风的暖心结构已基本建立,但该暖心的建立并未同化与温度相关的变量,而是通过径向风和反射率的“新息”向量对温度场进行调整,说明EnSRF“流依赖”的背景误差协方差能够正确反映物理量的相关关系。对比3种方案可以看出,物理约束扰动方案的位温垂直结构(图8c)比其他两种方案的(图8a、b)更加平滑,该方案更好地建立了雷达径向数据与模式变量间的相关关系。从绝对风速可以看出,分析循环末端全场随机扰动方案产生的台风左侧风速明显偏弱(图8b),而物理约束扰动方案则抓住了该侧的大风速状况。

图7 分析循环末端反射率(阴影;单位:dBz)、海平面气压(等值线;单位:hPa)、风场(箭矢;单位:m/s)的比较(图 b、c、d 中,红圈表示雷达体扫范围,虚线表示垂直剖面位置) a.观测;b.SRVF;c.SMVF;d.SPVFFig.7 Comparison of reflectivity(shadings;units:dBz),sea level pressure(contours;units:hPa)and wind field(vectors;units:m/s)at the end of analytical cycle(In figures b,c,d,red ring denotes radar’s covering and dashed line is position of cross section) a.observation;b.SRVF;c.SMVF;d.SPVF
4.2.2 台风强度、路径及降水预报
分析循环结束后进行12 h确定性预报,图9给出了台风中心气压及最大风速的时间序列。3种初始扰动方案产生的台风中心气压在10日06时均比最佳估计偏低,预报1 h后中心气压明显升高(图9a);而最大风速则明显减小(图9b)。这主要是由于雷达资料的观测范围有限,对大尺度环境场的调整能力偏弱,同时分析次数较少,模式中物理要素的配置关系不够好,模式动力过程将逐步调整这种不适应。就不同的初始扰动方案来看,由于物理约束扰动方案能够获得更好的先验RMSE,所以它在整个确定性预报中获得了更好的强度预报结果。
图10给出了12 h台风路径的预报,经过7次间隔30 min的分析循环,台风位置被不断修正,分析循环末端略有偏差。对比这3种试验可知,在登陆前SRVF的路径预报要优于SPVF和SMVF,表明RandomCV扰动方案对尺度较大的大气运动调整要比其他两种方案好,但台风登陆后,由于地形、地表摩擦造成台风动力、热力状况改变,小尺度作用逐渐超过大尺度环流场作用,SRVF的预报路径要明显比最佳估计偏北。从这一点来看,将来可以进一步考虑构造具有不同尺度的扰动叠加到背景场中。从整个12 h的路径来看,尺度较小的全场随机扰动和物理约束扰动对路径的预报效果更好,但后者在预报后期更加接近最佳估计路径。

图8 分析循环末端位温(实线;单位:K)和绝对风速(阴影;单位:m/s)的垂直结构(纬向穿过台风中心)a.SRVF;b.SMVF;c.SPVFFig.8 Vertical structure(zonally crossing typhoon center)of potential temperature(solid lines;units:K)and absolute velocity(shadings;units:m/s)at the end of analytical cycle a.SRVF;b.SMVF;c.SPVF
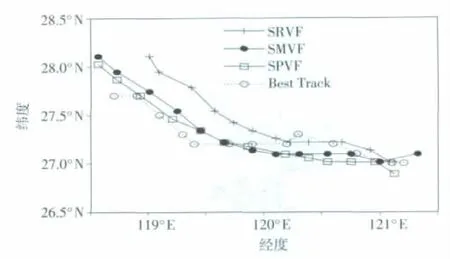
图10 预报台风路径和最佳估计路径的比较Fig.10 Comparison of typhoon track forecasts with the best estimated track
图11给出了实况、同化试验6 h累积降水的比较(实况降水使用TRMM卫星的定量降水估计作为海上无站点降水的补充)。由图11a、图10可知,降水主要发生在台风移动路径的右侧,呈现很强的不对称性(余贞寿等,2012)。3个同化试验基本再现了台风的螺旋雨带,海岸附近呈现出降水大值中心,同时也捕捉到了“桑美”台风降水的不对称性,但陆地上的降水落区要较实况范围偏小。对比同化试验预报结果发现,相对SPVF、SMVF而言,SRVF的螺旋雨带呈现出多中心的结构特征,6 h累计降水量较实况偏小。SPVF和SMVF预报的降水落区分布相近,仅在临近登陆前的部分地区SMVF降水量较SPVF偏大,两者均抓住了沿岸附近的大值中心,但中心降水量较实况偏高。总体而言,SPVF试验较好地抓住了近海岸降水的大值中心,同时未出现台风移动路径中产生过大降水的状况。
5 结论与讨论

图912 h预报的台风中心气压(a)和台风最大风速(b)Fig.9 The 12 h forecasts of typhoon(a)center pressure and(b)maximum wind speed
本文提出一种基于物理约束的初始扰动新方案,并利用台风“桑美”近海登陆过程的多普勒雷达资料进行集合卡尔曼滤波同化试验,对比新方案与广泛应用的RandomCV方案和全场随机扰动方案对同化及预报过程的影响,得到以下结论:

图 116 h 累计降水量(阴影;单位:mm)的比较 a.观测;b.SRVF;c.SMVF;d.SPVFFig.11 Comparison of 6 h accumulated rainfall(shadings;units:mm) a.observation;b.SRVF;c.SMVF;d.SPVF
1)新方案能够获得更好的“新息”平均和较为稳定的集合离散度,同化过程能够更多地利用反射率观测资料,调整的集合平均和扰动结构也更为合理。
2)经过3 h的集合Spin-up,物理约束扰动的先验均方根误差明显较RandomCV方案和全场随机扰动方案好;就反射率而言,3种方案分析前后的均方根误差差异较为显著,但物理约束扰动的表现效果总体优于其他两种初始化方案,在相同集合Spinup基础上,物理约束扰动能够得到更为合理的结果。
3)不同的扰动方案,经EnSRF同化均可修正台风中心位置,对调整模式中台风的温压结构以及对台风路径和降水预报起到积极作用,但物理约束扰动方案对台风路径、中心气压和最大风速的预报结果更为理想。
本文提出的物理约束扰动方案针对个例取得了良好的结果,但该方案还不能很好反映出各尺度扰动的信息,下一步考虑利用业务系统集合预报结果作为样本构造更为合理的扰动势函数和流函数。此外,新方案依然存在虚假对流的情况,考虑从雷达观测出发将该方案生成的扰动场限制在实际对流区域内,以降低不合理扰动激发的虚假对流。
崔哲虎,程明虎,乌秋力,等.2005.快速中值滤波方法及其在Doppler雷达资料处理中的应用[J].高原气象,24(5):727-731.
闵锦忠,陈杰,王世璋,等.2011.WRF-EnSRF同化系统的效果检验及其应用[J].气象科学,31(2):135-144.
余贞寿,闵锦忠,钟建锋,等.2012.超强台风“桑美”(0608)近海观测特征研究[J].科技通报,28(3):21-27.
Aksoy A,Dowell D C,Snyder C.2009.A multicase comparative assessment of the ensemble Kalman filter for assimilation of radar observations.PartⅠ:Storm-scale analyses[J].Mon Wea Rev,137(6):1805-1824.
Anderson J L.2001.An ensemble adjustment Kalman filter for data assimilation[J].Mon Wea Rev,129(12):2884-2903.
Barker D M.2005.Southern high-latitude ensemble data assimilation in the Antarctic mesoscale prediction system[J].Mon Wea Rev,133(12):3431-3449.
Barker D M,Huang W,Guo Y R,et al.2004.A three-dimensional variational data assimilation system for MM5:Implementation and initial results[J].Mon Wea Rev,132(4):897-914.
Evensen G.1994.Sequential data assimilation with nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J].J Geophys Res,99(5):143-162.
Evensen G.2003.The ensemble Kalman filter:Theoretical formulation and practical implementation[J].Ocean Dynamics,53:343-367.
Gao J D,Xue M,Shapiro A,et al.1999.A variational method for the analysis of three-dimensional wind fields from two Doppler radars[J].Mon Wea Rev,127(9):2128-2142.
Gao J D,Xue M,Keith B,et al.2004.A three-dimensional variational data analysis method with recursive filter for Doppler radars[J].J Atmos Oceanic Tech,21(3):457-469.
Hamill T M.2001.Interpretation of rank histograms for verifying ensemble forecasts[J].Mon Wea Rev,129(3):550-560.
Hollingsworth A,Lonnberg P.1986.The statistical structure of shortrange forecast errors as determined from radiosonde data.PartⅠ:The wind field[J].Tellus,38A:111-136.
Li Y Z,Wang X G,Xue M.2012.Assimilation of radar radial velocity data with the WRF hybrid ensemble-3DVAR system for the prediction of hurricane Ike(2008)[J].Mon Wea Rev,140(11):3507-3524.
Lindskog M,Salonen K,Jarvinen H D,et al.2004.Doppler radar wind data assimilation with HIRLAM 3DVAR[J].Mon Wea Rev,132(5):1081-1092.
Lorenc A C.1992.Iterative analysis using covariance functions and filters[J].Quart J Roy Meteor Soc,118(4):569-591.
Meng Z Y,Zhang F Q.2007.Tests of an ensemble Kalman filter for mesoscale and regional-scale data assimilation.PartⅡ:Imperfect model experiments[J].Mon Wea Rev,135(4):1403-1423.
Smith P L,Myers C G,Orville H D.1975.Radar reflectivity factor calculations in numerical cloud models using bulk parameterization of precipitation[J].J Appl Meteor,14(6):1156-1165.
Snook N,Xue M,Jung Y S.2011.Analysis of a tornadic mesoscale convective vortex based on ensemble Kalman filter assimilation of CASA X-band and WSR-88D radar data[J].Mon Wea Rev,139(11):3446-3468.
Sun J Z,Crook N A.1997.Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint.PartⅠ:Model development and simulated data experiments[J].J Atmos Sci,54(12):1642-1661.
Sun J Z,Crook N A.1998.Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint.PartⅡ:Retrieval experiments of an observed Florida convective storm[J].J Atmos Sci,55(5):835-852.
Tong M J,Xue M.2005.Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model:OSS experiments[J].Mon Wea Rev,133(7):1789-1807.
Tong M J,Xue M.2008.Simultaneous estimation of microphysical parameters and atmospheric state with simulated radar data and ensemble square root Kalman filter.PartⅠ:Sensitivity analysis and parameter identifiability[J].Mon Wea Rev,136(5):1630-1648.
Whitaker J S,Hamill T M.2002.Ensemble data assimilation without perturbed observations[J].Mon Wea Rev,130(7):1913-1924.
Zhang F Q,Weng Y H,Sippel J A,et al.2009.Cloud-resolving hurricane initialization and prediction through assimilation of Doppler radar observations with an ensemble Kalman filter[J].Mon Wea Rev,137(7):2105-2125.
Zhang J,Wang S X.2006.An automated 2D multipass Doppler radar velocity dealiasing scheme[J].J Atmos Oceanic Tech,23(9):1239-1248.

