基于SIDWT的多模态脑部医学影像融合算法
郭昕刚,王宏志,王 宇
(1.长春工业大学计算机科学与工程学院,吉林 长春 130012;2.长春理工大学电子信息工程学院,吉林 长春 130022)
图像融合是近年来图像处理和机器视觉领域人们重点研究的一个方向。特别是在医学领域,为了能让医生更直观更准确地对病灶进行判断和治疗,往往需要将来自不同成像设备的医学图像进行综合分析。而医学影像的成像原理、影像特点等都各不相同,例如,CT的密度分辨率极高,图像逼真清晰,解剖关系明确,对病变的定位和定性好,易于显示腹内实质性脏器的组织结构,但是含有放射性,空间分辨率较差,曝光时间长,易产生伪影。而MRI对脑和软组织成像分辨率极佳,多方位,多参数成像,具有流空效应,能对血管进行检查,可进行形态学,组织化学和生物化学方面的研究,但是钙化特征成像效果差,扫描信号采集时间长,危重症病人不能进行检查。通过对CT影像和MRI影像进行融合,为医生提供了更直观、更全面的生理信息,给病变的判断和治疗带来了帮助。
小波变换是在传统傅里叶分析的理论基础之上发展起来的,它的应用十分广泛,尤其是在图像处理领域,小波变换实现了时域和频域的相互转化,利用多种运算工具,多尺度全方位的分析信号,获取有用信息,作为一种极其有效的处理信号的工具,常被用于图像融合。虽然小波变换的融合效果相对比较理想,但在融合的过程中仍存在一些问题,如二维离散小波变换在分解和重建信号时不具有平移不变性,导致在融合图像的奇异处产生伪吉布斯现象,还有小波系数的选择是否恰当等问题[1]。考虑到以上不足,本文基于平移不变小波变换,提出了新的融合规则,实验结果表明,新方法能充分地保留图像的边缘和细节信息,融合效果更理想。
1 基于SIDWT的图像融合方法
1.1 平移不变离散小波变换原理
小波分解的Mallat算法存在下采样环节,不具备平移不变性,在融合结果中容易引入虚假信息,如振铃和混叠效应。为了克服上述不足,文献[2]提出平移不变离散小波变换(SIDWT)算法。以一维信号为例对其变换原理描述如下:
平移不变离散小波变换(SIDWT)的各个步骤都把原始数据变形,变成两部分,小波序列wi(n)部分和尺度序列si(n)部分。

si(n)会被用于下一层分解的输入信号,s0(n)=f(n),f(n)为输入信号。在原始滤波器g(k)及h(k)的序列间加上一定的“0”值就获得了第i层的高通滤波器g(2i·k)以及低通滤波器h(2i·k)。h(k)和g(k)的关系为

式中:H(z)是h(k)的z变换,G(z)是g(k)的z变换。这就是SIDWT的整个分解步骤。对比之前提到过的离散小波变换,因为没有了下采样,SIDWT具备平移不变性。二维图像信号的分解可以通过连续进行一维分解,分别在图像的行及列上来完成。图1是一幅医学图像经过二级SIDWT分解得到的各频带子图像。
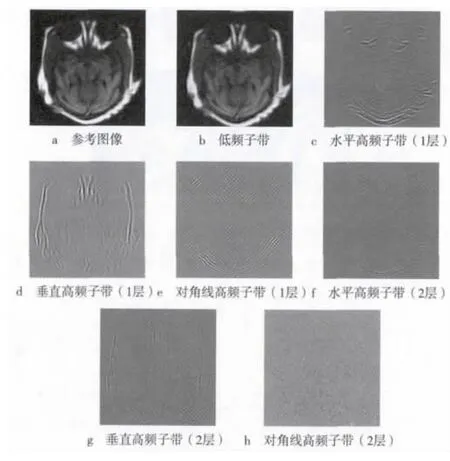
图1 二层SIDWT分解各频带子图像
由图1可以看出,一幅图像经过N层SIDWT分解,可得到一个低频子带以及3N个高频子带,而且新得到的高低频子带图像与原始图像尺寸相同,可以减小配准误差对融合结果的影响。
1.2 低频子带融合规则
经过SIDWT分解以后,需要对不同的频带设计融合规则进行融合。在结合小波相关理论的融合中,低频部分代表了被测目标的绝大部分能量,更接近于被测目标的整体信息。所以低频分量很大程度上关系到图像质量的恢复情况[3]。由于图像的局部特征往往不是由单个像素的变换系数所能表示的,所以采用基于窗口的融合规则。设低频子带中以某点(x,y)为中心的m ×n邻域用I(x,y)表示,文献[4]提出了一种基于区域对比度的图像清晰度评价算法,本文基于其定义的区域对比度构造低频子带的融合规则。局部区域对比度定义为

式中:maxI(x,y)与 minI(x,y)分别代表某点 (x,y)的m×n邻域内低频系数的最大值和最小值。显然邻域局部对比度越大,中心像素点周围灰度变化越剧烈。因此采用如下融合策略

式中:DA和DB分别表示在源图像A和B的低频子带中以某点(x,y)为中心的局部区域对比度;LA,LB与LF分别表示源图像A,B与融合图像F的低频子带系数。
1.3 高频子带融合规则
图像融合就是从源图像的高频子带中获取最能代表图像纹理细节的边缘信息,小波变换的高频系数的选择对于保留图像的边缘特性有很重要的作用。高频方向子带中的显著大系数,对应源图像中的强边缘,强区域轮廓等,而较小的系数则对应源图像中较为平滑的区域。为了更准确地突出图像的边缘纹理细节信息,去除冗余,将图像划分为边缘区和平滑区两部分,针对不同区域采取不同的融合策略。
小波变换后的高频系数反映了图像边缘的变化与分布。设H(i,j)为图像经小波分解后的某高频系数值。S为该高频子带系数的标准差。对相应高频子带系数进行二值化可得

若d(i,j)为“1”,则认为该系数是活跃的;为“0”,则是非活跃的[5]。边缘区由于图像灰度变化剧烈,则二值化后“1”的个数多;而平滑区由于图像灰度变化平缓,则二值化后“1”的个数就远少于边缘区。因此对高频子带进行均匀分块,每个高频子块有与之相对应的二值化高频系数子阵。可以通过统计该子阵里“1”的个数之和来判断该高频子块的区域属性。用SIDWT对源图像进行3层分解,分别得到3个水平方向的高频子带(HLi)、垂直方向的高频子带(LHi)和对角线方向的高频子带(HHi),i为分解层数。对所有各高频子带进行均匀分块,分块大小为m×n,定义各高频子带中第K个高频子块的平滑度Ck为

由于噪声主要存在于HHi中,所以仅对HLi与LHi子带进行统计,去除噪声的影响。CHLik为第i层分解得到的HLi子带中,第K个高频子块对应的二值化高频系数子阵中“1”的个数之和。同理,CLHik为LHi子带中第K个高频子块对应的二值化高频系数子阵中“1”的个数之和。求出平滑度以后,设定阈值T,待融合的两幅源图像分别为A和B,具体融合方法如下:
1)如果CAK>T或者CBK>T,说明该高频带子块对应着源图像的边缘区域,为了更加突出边缘细节信息,采用系数极大值法进行融合。即

式中:Ak(i,j)与Bk(i,j)分别对应着两幅源图像在同一分解层的同一高频方向子带上,坐标位置(i,j)点处的系数值;Fk(i,j)表示融合后的高频子带系数值。
2)如果不满足上述条件,则说明该高频带子块对应着源图像的平滑区域。考虑该区域像素的局部相关性,采用文献[6]提出的基于局部信息熵的融合规则。对两幅源图像A和B的处于同一分解层上,相同方向高频子带中的第k个子块,分别按照文献[6]的公式求得各自的局部信息熵,记为HAk与HBk,然后按照下式进行融合。Ak,Bk与Fk分别代表源图像A,B与融合图像F相对应的高频子带中第k个子块矩阵。
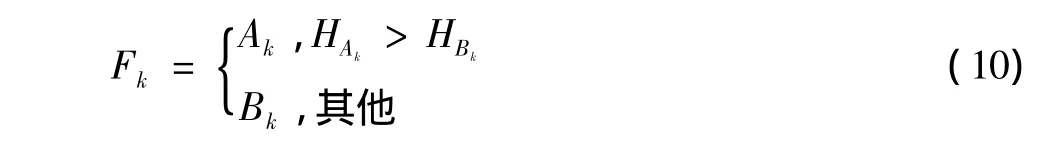
最后对融合后的高、低频系数进行SIDWT逆变换,得到最终的融合图像。
2 融合实验
图2与图3是两组已配准的颅脑部位的CT及MRI融合实验图像。图a均为病人的原始CT图,显示了清晰的骨组织结构;图b均为该病人的原始MRI图,可以显示清晰的软组织;图c均为低频采用加权平均法,高频采用本文融合规则得到的融合图像(算法1);图d均为低频采用本文的融合规则,高频采用局部区域能量最大融合规则得到的融合图像(算法2);图e为本文的融合方法得到的融合图像。图b与图c均采用Daubechies小波系中的DB4小波基,三种方法对源图像都进行三层分解。
目视结果可以看出,图2与图3中利用本文算法得到的融合图像能够同时清晰显示颅脑的骨组织和软组织,优于其他两种基于小波变换的传统融合算法。采用图像的熵、标准差、互信息[7]作为客观评价指标对上述方法得到的融合图像质量进行评价,见表1和表2。


图3 第二组实验图像及融合结果

表1 第一组实验图像评价数据

表2 第二组实验图像评价数据
从上表可以看出,采用本文算法的算法熵、互信息和标准差都达到最大值,从客观评价上证明了本文算法的融合质量最佳。
3 小结
图像融合在医学图像分析和诊断上具有重要的应用价值。基于平移不变小波变换提出了一种新的图像融合算法,克服了传统小波变换不具备平移不变性导致融合图像的失真。对低频子带采用局部区域对比度,尽可能多地保留了原始图像的信息。对高频子带定义了平滑度,并利用平滑度把高频子带分割成不同的区域,针对不同区域采取不同的融合策略。该方案有效地保持了源图像的边缘及细节信息,去除了冗余。实验结果表明,与传统的小波变换融合算法相比,无论从主观融合效果,还是客观评价指标,该方法的图像融合效果都优于传统的小波变换融合方法。
[1]王珂,欧阳宁.图像融合技术及评价方法[J],电视技术,2007,31(1):20-23.
[2]ROCKINGER O.Pixel level fusion of image sequences using wavelet frames[C]//Proc.the 16th Leeds AnnualStatisticalResearch Workshop.Leeds,UK:Leeds University Press,1996:149-154.
[3]HALL D,LLINAS J.An introduction to multisensor data fusion[J].Proceedings of the IEEE,1997,85(1):6-23.
[4]张亚涛,吉书鹏,王强锋,等.基于区域对比度的图像清晰度评价算法[J],应用光学,2012,33(2):293-299.
[5]RAMOS M,HEMAMI S,TAMBURRO M..Psycbovisually-based multiresolution image segmentation[C]//Proc.IEEE Int.Conf.Image Processing 1997.Santa Barbara,CA:IEEE Press,l997:66-69.
[6]WAN T,CANAGARAJAH N,ACHIM A.Segmentation-driven image fusion based on alpha-stable modeling of wavelet coefficients[J].IEEE Trans.Multimedia,2009,11(4):624-633.
[7]QU G,ZHANG D,YAN P.Information measure for performance of image fusion[J].Electronics Letters,2002,38(7):313-315.

