图像配准中特征点检测算法的探讨
纪利娥,杨风暴,王志社,陈 磊
(中北大学信息与通信工程学院,山西 太原 030051)
图像配准是指将不同条件(时间、视角等)或不同传感器下获得的同一场景的两幅或多幅图像进行匹配的过程,即寻找一种空间映射关系,使两幅图像中代表同一目标的对应点达到空间位置上的一致[1-2]。它是图像融合、目标识别等技术的关键前提,在医学、军事及遥感等领域具有广泛的应用。
基于特征点的配准方法是研究的热点,它主要包括特征点提取、特征点匹配、计算变换模型参数和图像变换与插值4个部分。其中,特征点检测是图像配准的重点和难点,特征点提取的好坏直接影响着图像配准的精度和效率[3]。近几年,国内外出现了许多特征点检测方法,然而对这些方法应用于图像配准这个环境中的实际效果如何,提取的特征点是否有利于图像配准,以及各种特征点检测算法的性能如何,都缺乏相应的分析与比较,对特征点提取方法也缺乏相应的评价标准。
本文主要从特征点检测与评价这两个方面出发,详细介绍了目前主流的特征点检测算法,并对特征点提取算法的评价标准作了一定的具体说明。通过实验,比较了各种算法的性能,为不同应用情形下特征点提取方法的选择提供有力的参考。
1 特征点检测方法
图像配准中的特征点是指对旋转、平移、缩放、光照等变换具有不变性,对噪声的敏感性也比较小,在不同成像条件下仍能保持一致性。
常用的特征点检测算法可以归纳为以下三类:
1)基于边缘点的提取方法:如LOG检测、Canny算子、基于小波变换的提取方法、基于NSCT(Nonsubsampled Contourlet Transform)的鲁棒性特征点等。
2)角点检测方法:主要包括基于边缘和基于灰度的方法,第一类需对边缘进行编码,对图像分割和边缘提取要求比较高,难度和计算量较大;第二类方法直接对图像灰度进行操作,主要是通过计算点的曲率及梯度来检测角点,此类方法主要有Moracec算法、Forstner算法、Harris算法、Susan算法等。
3)高效斑点检测算法:如SIFT(Scale Invariant Feature Transform)算法、SURF(Speeded Up Robust Features)算法等。
本文将对上述3类特征点中一些典型算法做详细的分析与比较。
1.1 基于NSCT的特征点检测方法
非下采样轮廓波变换(NSCT)是Cunha和Zhou等人[4]提出的一种多尺度多分辨率分析手段,具有快速变换、多尺度、多方向、平移不变、边缘保持、频率不混淆以及变换后图像大小不变的优点;在NSCT域中,尺度内、尺度间的系数都具有一定的相关性,噪声和细节在尺度间、尺度内各方向分布也具有不同的特点。
基于NSCT的特征点检测方法[5]步骤如下:
1)对图像进行N级NSCT变换,得到低频子带图像及各尺度L个方向上的高频方向子带系数矩阵。
2)对于高频分量,求相邻尺度同一方向子带的差值模值,得到L个差值子带图像。
3)对于所获得的差值子带图像,针对图像每一个像素点位置,进行模极大值检测,得到一幅NSCT模极大值图像。
4)在NSCT模极大值图像上利用硬阈值Th去除非显著的特征点,如NSCT模极大值大于阈值Th,则保留这些点;其中,Th=c(δ+μ),c是用户自定义参数,δ和μ是NSCT模极大值图像的标准方差和均值。
5)以4)保留下来的模极大值点为中心,在w×w的邻域内进行非极大值抑制,最后得到的点作为所提取的特征点。
基于NSCT的特征点提取方法的特点:
1)该算法采用多尺度空间思想,充分利用了NSCT域尺度内、尺度间系数的相关特性这一特点,能有效地抑制噪声、增强特征点;
2)NSCT具有很好的方向性,提取的特征点多位于图像的边缘、拐角处,具有很高的精度且鲁棒性强,很好地表征图像的显著特征;
3)NSCT是全局变换,由于其非下采样,变换后的图像大小不变,与小波变换相比,计算速度慢,对图像配准而言缺乏实时性。
1.2 基于灰度的角点检测方法
1)Harris算法
Harris角点[6]检测算法的思想是:使图像中的一个局部小区域在各个方向做微小移动,计算该区域内能量的变化,当该变化值超过一定阈值时,就认为该小区域内的中心像素点为角点。
Harris算法为

当某点的响应值R大于阈值t,进行局部极大值抑制,获得最终的角点。
Harris算法的特点是:
(1)算法只用到了灰度一阶差分,计算简单,速度快。
(2)算法通过计算图像每个位置的响应值,在合适的领域内选择最优点,提取的点特征均匀合理,在纹理信息丰富的区域,角点的数量较大,反之亦然。
(3)通过对极值点进行统一排序,根据时间和精度要求选取数量合理的最优角点。
(4)Harris算子对图像平移旋转和光照变化具有不变性,能够稳定地检测特征点;对噪声比较敏感,在信噪比低的条件下,特征点数量明显增加,加大了特征匹配的难度;且不具有尺度不变性和仿射不变性。
为了使Harris算子具有尺度不变性,把尺度空间理论引入到 Harris特征点检测上。Harris-Laplace[7]算子检测的特征点具有尺度不变性。
Harris-Affine[7]是一种新颖的检测仿射不变特征点的方法。在大尺度缩放变化的情况下,具有很好的性能;由于初始点检测和仿射区域的归一化,计算具有一定的复杂度。
2)Susan算法
Susan算法是由S.M.Smith等人[8]提出的,主要用来计算图像中的角点特征。SUSAN角点提取法主要有以下3步:
(1)计算核值相似区USAN的大小n( r0)
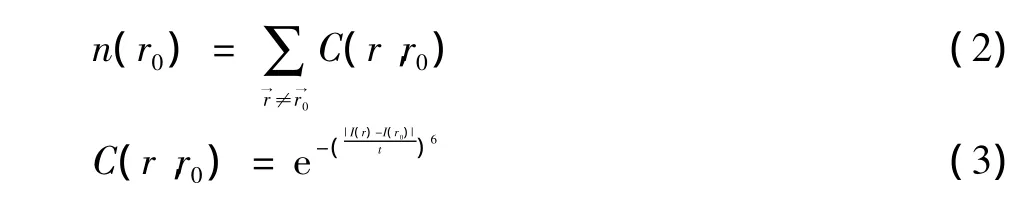
式中:r为模板内除核以外的其他位置;r0为模板核的位置;I为像素灰度值;t表示所能检测角点的最小对比度,其值越小,提取的角点越多;C(r,r0)表示灰度比较的结果。
(2)计算角点响应值R( r0)

式中:g为固定阈值,通常g=nmax/2;nmax为模板的大小减1,其大小不仅决定了角点的个数,也决定所检测角点的尖锐程度。
(3)去除虚假角点,并利用非极大值抑制确定角点:对于那些与正确角点相关的USAN区域,其重心位置远离模板的中心位置,利用加权法求重心,计算核到重心的距离,距离比较大,则认为该角点是候选角点。

Susan算法的特点:
(1)无须梯度计算,提高了算法的效率;
(2)具有积分特征,对局部噪声不敏感,抗干扰能力强;
(3)对角点的检测比对边缘的检测效果好,且特征点定位比较准确;
(4)针对模糊或者强噪声图像的检测结果,无论准确率还是数量,都不太理想;
(5)该算法对阈值较敏感,选取合适的参数对算法结果影响很大,同时会出现漏检和误检测角点。
1.3 高效斑点检测方法
1)SIFT算法
SIFT算法是Lowe[9]提出的一种尺度不变特征点检测方法,计算步骤如下:
(1)特征点检测
将不同尺度的高斯差分核与图像进行卷积,在生成的高斯差分尺度空间(DOG)检测极值点,这样提取的特征点较稳定。

式中:k为两相邻尺度空间倍数的常数;G(x,y,δ)为高斯空间函数。
将每一个采样点与它同尺度的8个相邻点和上下相邻尺度对应的9×2个点进行比较,在尺度空间和位置空间寻找局部极值点,视为候选点。然后通过子像元插值法精确定位特征点的位置及尺度,同时去除低对比度的特征点和不稳定的边缘响应点。
作为候选特征点,通过拟合三维二次函数以精确定位特征点的位置和尺度,同时去除低对比度的特征点和不稳定的边缘响应点。
(2)特征点描述
根据检测到的特征点的局部图像结构求得一个方向基准,使得特征点描述子对图像的旋转具有不变性。(x,y)处梯度的模值和方向公式如下

式中:L所在的尺度为每个特征点所在尺度。
为确保旋转不变性,将高斯图像坐标轴旋转为特征点的主方向。取以特征点为中心的4×4子区域,在每个子区域计算8个方向的梯度强度信息,共有4×4×8=128维的SIFT特征向量。此时该向量具有尺度及旋转不变性。再对特征向量归一化,可去除光照变化带来的影响。
SIFT算法的特点:
(1)在多尺度空间采用DOG算子检测关键点,相比传统的基于LOG算子的检测方法,运算速度大大加快;
(2)该算法提取的特征点较稳定,能够在图像仿射变换、视角变换及噪声等条件下具有很好的匹配能力;
(3)传统的SIFT算法维数较高,计算量大,速度慢;
(4)SIFT提取的特征点较多,使匹配时搜索范围大,增加了匹配时间和错匹配的概率。
针对SIFT算法速度较慢的问题,Ke等人[10]提出了PCA-SIFT算法,通过主成分分析降低了特征向量的维数,使计算复杂度下降。
2)SURF算法
Bay等人[11]通过将积分图像和Haar小波相结合,提出了SURF算法,进一步提高了特征提取的速度。主要包括两个部分:特征点检测和描述。
(1)特征点检测
SURF算法通过计算Hessian矩阵行列式的局部极值来检测特征点的位置。
设图像I中一个点X(x,y),在点X处,尺度为δ的Hessian矩阵H(X,δ)为

式中:Lxx(X,d)是图像 I中点 X与高斯二阶滤波∂2g(δ)/∂x2的卷积;Lxy(X,d)和 Lyy(X,d)的含义类似。
将盒子滤波器与图像进行卷积,其结果分别为Dxx,Dxy和Dyy,则Hessian矩阵的行列式可简化为

通过不同尺寸盒子滤波模板与积分图像求取Hessian矩阵行列式的响应图像,并在响应图像上进行3D非最大值抑制,求取各种不同尺度的斑点。
(2)特征点描述
首先确定SURF描述子的主方向以确保其旋转不变性。以特征点为中心,取半径为6δ(δ为特征点所在尺度)的区域作为其邻域,直方图统计邻域内各点的梯度和方向。以π/3为步长,找到具有最大分布响应的角度,将其作为该特征点的主方向;确定大小为20δ的矩形区域,将其划分为4×4的子区域,在每一个子区域内提取特征V

式中:dx,dy分别表示Harr小波在水平和垂直方向的响应值。
这样,每个特征描述子都由4×4×4=64维的特征向量组成。通过对特征向量进行归一化来实现对光照的不变性。
SURF算法的特点:
(1)SURF算法引入积分图像和盒子滤波器,在运算速度上比SIFT要快3倍左右,适用于图像分辨率变化较大的情况;
(2)对尺度、旋转、光照及视角变化等具有较强的鲁棒性和稳定性;
(3)在同一情况下,所提取的特征点数量少于SIFT特征点,综合性能优于SIFT算法。
2 特征点检测方法评价
特征点提取是图像配准的重要步骤,只有保证特征点准确可靠,才能进行有效配准。因此,不仅要通过主观视觉对特征点进行判断,还要通过客观指标对特征点进行准确评价。
在图像配准这个应用环境中,特征提取方法的好坏有其特定的涵义:特征点的数量要适中,特征点过多会给后续的特征匹配带来严重的运算负担,特征点过少可能无法满足变换模型的计算,且影响配准的精度;对于不同传感器图像及图像的不同变化,特征提取方法要有一定的适应性,且特征点要保持一定的不变性,才能使从不同图像提取的特征点能够精确匹配。综上所述,本文从3个方面对特征点检测方法进行评价。
1)特征点匹配率
特征点匹配率是指特征点匹配点对数与参考图像所有的特征点数之比。对于相同的实验图像,特征点匹配率越高,特征检测算法的性能越好。
2)检测速度
通过特征点检测所用时间来评价算法的速度。对于相同的图像,在相同的计算条件下,计算时间长说明特征检测算法速度慢。
3)不变性
对图像的旋转、平移、光照、仿射、噪声等变化,所提取的特征点应具有一定的不变性,才能保证不同图像之间的配准精度。
3 实验结果与分析
本文采用MATLAB 7.0对上述特征点检测算法进行实验。
3.1 Harris算法与Susan算法特征点检测比较
Harris算子和Susan算子在各种情况下的特征点检测结果如图1、图2所示,实验图像大小为169×169。


从上述实验结果可以看出,这两种特征点检测算法对图像旋转都具有一定的适应性,但Harris算法具有明显的优势;在噪声存在的情况下,特征点都明显增多。表1比较了算法的实时性及抗噪声能力,从表1可以看出Harris算子由于使用梯度,速度较慢,对灰度和几何变换的适用性稍优于Susan算子。

表1 Harris算子与Susan算子性能比较
3.2 SIFT算法与SURF算法特征点检测比较
本文在保持实验条件、主要参数一致的基础上,从特征点检测时间、特征点个数以及视角、光照和仿射变化下的匹配率这些方面对这两种算法进行对比,图3显示了两种算法在主要参数(组octaves=4,层levels=4)相同的情况下对同一幅实验图像提取的特征点情况,并通过表2对这两种算法的性能进行比较,实验图像大小为205×305。


表2 SIFT算法与SURF算法性能比较
从表2可以看出,SURF比SIFT在时间上有很大的提高;对于图像的视角、光照及仿射变化,这两种算法都具有一定的适应性;SURF检测的特征点明显不如SIFT丰富,但匹配率却比SIFT高。从实验结果可以看出:SURF在综合性能上要优于SIFT算法。
4 小结
基于特征点的图像配准方法是图像配准领域很重要的研究方向。特征点检测是图像配准的关键技术,特征点的好坏直接影响着后续图像配准的精度和效率。现有主流的特征点检测方法,都有其一定的局限性。本文对典型的特征点检测算法的优缺点进行详细的分析与比较,并给出了特征点评价的方法。
从图像配准的角度出发,对于特征点的提取,必须要考虑它的实时性、高精度和鲁棒性。随着图像配准实际应用的需求,对图像特征点提取方法必须进行深入研究,提出性能好的新方法,使基于特征点的图像配准方法具有良好的发展前景。
[1]赵芹,周涛,舒勤.基于特征点的图像配准技术探讨[J].红外技术,2006,28(6):327-330.
[2]刘琼,倪国强,周生兵.图像配准中几种特征点提取方法的分析与实验[J]. 光学技术,2007,33(1):62-67.
[3]GUARNERI I,GUARNERA M,LUPICA G,et,al.Image registration method for consumer devices[J].IEEE Trans.consumer electronics,2005,51(3):215-219.
[4]CUMHA A,ZHOU Jianping,DO M.The nonsubsampled contourlet transform:theory,design,and application[J].IEEE Trans.Image Processing,2006,15(10):3089-3101.
[5]CHAHIRA S,MOURAD B,YOUCEF B,et al.Robust feature points extratction for image registration based on the nonsubsanmpled contourlet transform[J].Int.J.Electron.Commun.(AEU),2009(63):148-152.
[6]HARRIS C,STEVEN M.A combined corner and edge detector[C]//Proc.the fourth Alvey Vision Conference.Manchester,UK:[s.n.],1988:147-151.
[7]MIKOLAJCZYK K,SCHMID C.Scale & affine invariant interest point detectors[J].International Journal of Computer Vision,2004,60(1):63-86.
[8]SMITH S,BRADY J.SUSAN-a new approach to low level image processing[J].International Journal of Computer Vision,1997,23(1):45-78.
[9]LOWE D.Distinctive image features from scale-ivariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[10]YE K,SUKTHANKAR R.PCA-SIFT:A more distinctive representation for local imagw descriptors[C]//Proc.Conference on Computer Vision and Patter Recognition.[S.l.]:IEEE Press,2004:511-517.
[11]BAY H,ESS A,TUYTELAARS T,et al.Speeded-up robust feature[J].Computer Vision and Image Understanding,2008,110(3):346-359.

