利用matlab计算与模拟点电荷对的电场

薛海国

(四川理工学院 理学院，四川 自贡 643000)

1 matlab 和点电荷系的电场

点电荷是电磁学中最简单的一种理想化模型。单个点电荷在空间某点所激发的电场强度大小和电势U =用电场线和等势面直观形象地来表示这两个物理量。电场线从正电荷(无穷远)出发终止于负电荷(无穷远)，电场线的切线方向代表该点的场强方向，电场线的疏密来表示电场的强弱。电场线和等势面处处垂直。

然而在真空中某点所激发的电场通常是由点电荷组或者连续带电体所激发。对于点电荷组在空间某点所激发的电场强度和电势，我们可以根据电场强度矢量叠加和电势标量叠加进行数值求解。比较有代表性的就是要求电偶极子在延长线上和中垂线上的E 和U。简单的点电荷系的模型还有两个等量同号点电荷系，两个不等量同号点电荷系等。但是如果空间带电体的数量多于两个，并且在空间有一定规律分布，我们虽然能求出E 和U 的数值，但由于电场线和等势面的抽象性和复杂性，此时就很难想象出空间的分布。

matlab 有强大的数学运算能力和绘图功能，能直接利用软件提供的函数，编写较简单的程序即可解决相应的物理问题。已有文献［1］［2］［3］对电偶极子、电四极子，多个点电荷系统的电势分布和矢量场图进行计算仿真。

2 等量同号点电荷电场中的E 和U

如图所示，等量同号点电荷在场点P(x，y)产生的电势为

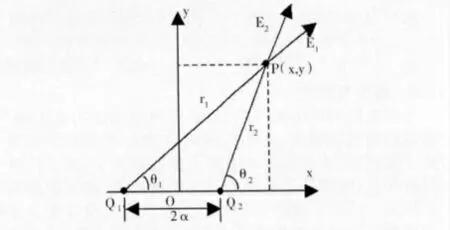
其中

E=－▽U，

其中，劈形算符为

在xy 平面上，场强只有两个分量

3 利用matlab 计算和模拟电场强度和电势

3.1 计算距离两个等量同号点电荷远处任一点的电位和场强

clear

＞＞syms q C0 r1 r2 x y U1 U2 a;

＞＞r1 =sqrt((x－a).^2 ＋y.^2);

＞＞r2 =sqrt((x ＋a).^2 ＋y.^2);

＞＞U1 =C0.* q./r1;U2 =C0.* q./r2;

＞＞U=U1 ＋U2;

＞＞Ex=－diff(U，x)，Ey=－diff(U，y)，AE=sqrt(Ex.^2＋Ey.^2)

运行结果

Ex =

1/2* C0* q/(x^2－2* x* a ＋a^2 ＋y^2)^(3/2)* (2* x－2* a)＋1/2* C0* q/(x^2 ＋2* x* a ＋a^2 ＋y^2)^(3/2)* (2*x ＋2* a)

Ey =

C0* q/(x^2－2* x* a ＋a^2 ＋y^2)^(3/2)* y ＋C0* q/(x^2 ＋2* x* a ＋a^2 ＋y^2)^(3/2)* y

AE =

((1/2* C0* q/(x^2－2* x* a ＋a^2 ＋y^2)^(3/2)* (2*x－2* a)＋1/2* C0* q/(x^2 ＋2* x* a ＋a^2 ＋y^2)^(3/2)*(2* x ＋2* a))^2 ＋(C0* q/(x^2－2* x* a ＋a^2 ＋y^2)^(3/2)* y ＋C0* q/(x^2 ＋2* x* a ＋a^2 ＋y^2)^(3/2)* y)^2)^(1/2)

在中垂线上时，x=0.键入:

x=0，

Ex=subs(Ex)，Ey=subs(Ey)，

返回:

Ex =0

Ey =2* C0* q/(a^2 ＋y^2)^(3/2)* y

在坐标原点时，x=0，y=0，键入:

x=0，y=0，

Ex=subs(Ex)，Ey=subs(Ey)

返回:

Ex =0

Ey =0

3.2 绘制距离两等量同号点电荷远处任一点的电位和场强分布图

clear

＞＞q=1.6e－19;C0 =9e9;l=3.0;

＞＞x=－5:0.5:5;y=x;

＞＞［X，Y］=meshgrid(x，y);

＞＞r1 =sqrt((X－l/2).^2 ＋Y.^2);

＞＞r2 =sqrt((X ＋l/2).^2 ＋Y.^2);

＞＞U=q.* C0.* (1./r1 ＋1./r2);

＞＞［Ex，Ey］=gradient(－U);

＞＞AE=sqrt(Ex.^2 ＋Ey.^2);

＞＞Ex=Ex./AE;Ey=Ey./AE;

＞＞subplot(1，3，1);

＞＞contour(X，Y，U，＇k－＇)

＞＞axis(＇square＇)，xlabel(＇x＇);ylabel(＇y＇);

＞＞title(＇等量同号点电荷的等位线和电场分布＇);hold on

＞＞quiver(X，Y，Ex，Ey，0.7)

＞＞plot(－l/2，0，＇ro＇，－l/2，0，＇r ＋＇)，plot(l/2，0，＇ro＇，l/2，0，＇r ＋

＇)

＞＞hold off，

＞＞subplot(1，3，2);meshc(X，Y，U);

＞＞subplot(1，3，3);meshc(X，Y，AE)

通过上面的图示，我们可以看出电场线从正电荷出发，终止在无穷远处。电场线与等势线垂直，任何两条电场线都不相交。当两个电荷的电量相等时，电场线和等势线对中垂线是对称的。

4 结束语

以点电荷的电势和电场强度模型，用matlab 指令直观形象地画出了两个等量同号点电荷的电场线和等势线的平面分布，电势和场强的空间分布。对于上述程序，稍加修改我们也可得到不等量，不同号的点电荷对的电场空间分布。

［1］王明美.一对点电荷电场的matlab 模拟实验［J］.合肥师范学院学报，2012，30(3).

［2］汤朝红.利用matla 模拟点电荷对的电场线分布［J］.广西物理，2012，33(4)

［3］孔祥鲲.基于matlab 构建点电荷系的电势和电场强度分布图［J］.实验技术与管理，2007，24(10)

［4］钱曦旭等著.MATLAB 及其在大学物理课程中的应用［M］.西安:陕西师范大学出版社，2006.