基于LabVIEW的电机振动信号分析
邹世明 张祥明
( 井冈山大学 机电工程学院,江西 吉安 343009)
1 LabVIEW 简述
LabVIEW 是美国NI 研发的一种基于G 语言的图形编程开发环境,是一种用图标代替文本行创建应用程序的图形化编程语言。用该种方式开发完成的程序,其构成文件大部分都是后缀名为vi 的文件,这些文件因其后缀而被叫做VI。VI文件一般有四个组成部分:首先是前面板,前面板主要的功能是交互,将使用者输入的数据和指令输送给另一个组成部分框图,而计算和分析结果也在前面板上以数字、图形或是表格等各式各样的方式表现出来。其次是框图部分,该部分中主要是负责将前面板接到的指令进行计算,然后将最终的计算结果传输给使用者。还有就是图标,图标是VI 文件的外在的图形符号,LabVIEW 为了满足使用者对图标的不同喜好,专门设置了图标编辑器,从而让使用者们能够自主的制作自己所欣赏的图标。最后的一个组成部分则是连线板,该部分是自定义输入和输出。以上四个部分共同组成了VI 文件,在彼此的相互配合下,使该文件的功能得到良好发挥。
2 振动信号的时域分析
常见的反映振动信号的基本特征参数有:均值μ、均方根Xrms、峰峰值φx。均值反映信号的静态分量,即常值分量。均方根也称作为有效值,它的计算方法是先平方、再平均、然后开方。峰峰值主要是针对周期稳态信号而言,对于随机信号无法确定。
(1)均值
振动信号的均值是样本函数x(k)在整个时间坐标上的积分平均,其物理含义为该振动信号变化的中心趋势,离散振动信号均值计算公式为
(2)均方根
振动信号的均方根是为信号的有效值,离散振动信号均方根计算公式如下:
(3)峰峰值
振动信号的峰峰值是信号最高正峰max{x(k)}到最低负峰min{x(k)}的距离,离散振动信号峰峰值计算公式为φx=max{x(k)}-min{x(k)}。
3 振动信号的频域分析
傅立叶变换作为平稳信号分析、处理的一项关键技术,能够将一个时域的问题通过傅立叶变换能转化成频域的问题来分析研究。设x(t)为t 的函数,并且满足狄氏条件,具体的计算式如下:X(f)=∫+∞-∞x(t)e-2πftdt。
连续傅立叶变换实现了测试信号从时域到频域的转换,在理论分析中具有很大的价值。虽然其功能强大,但是连续傅立叶变换也有自身的不足之处,它不能直接使用在计算机技术上,因为繁琐的计算限制了它的进一步发展。这种情况的改善是源于离散傅立叶变换的出现,离散傅里叶变换让数学方法与计算机技术进行了很好的融合,两者的融合使得工程的发展有了更大的保障依据。设x(k)为一时域数字序列,具体的计算方式如下
对于离散傅立叶变换,求出N 点x(k)需要N2次复数乘法,N(N-1)次加法运算。每次复数乘法要做四次实数乘法,两次实数加法运算。这样当N 很大时,所需的计算工作量也是相当可观的。为了进一步减少计算量,库利-图基于1965年提出了快速傅立叶算法,使用快速傅立叶变换,计算N 点离散傅立叶的计算量由N2次复数乘法降为Nlog2N 次复数乘法,计算强度明显降低。
4 电机振动信号检测分析
电机振动信号的由速度传感器检测电动机振动信号,从速度传感器检测到的电机振信号往往比较小,易受噪声影响,在用数据采集卡采集前,先要将微弱信号放大预处理,然后再利用数据采集卡进行数据采集,利用LabVIEW 中的分析函数和功能模块对特征信号值进行数字滤波以及进一步的分析处理,采用一定机制方法,如值域判定、时域判定、幅度谱判定、相位谱判定、功能判定和逻辑判定等作出评判,最后实现电机的健康诊断。当然由LabVIEW 软件开发完成的工作有数据采集、信号处理、健康诊断。其检测分析具体过程见图1 所示。

图1 振动信号检测分析框图
我们根据电机在正常运转时所产生的震动和噪声,对检测处得振动信号进行详细全面的检测,由于电机工作时要经历启动、加速、匀速、减速到停止各个工作阶段,为便于对电机的状态分析,对其匀速运转阶段的振动信号进行分析。其振动信号时域波形和频谱分析图如图2、图3 所示:
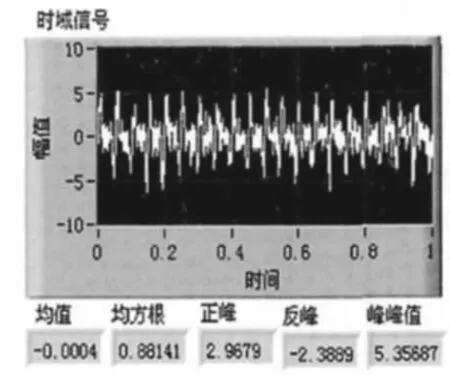
图2 振动信号时域波形

图3 频谱分析图
5 结论
LabVIEW 提供了丰富的图形化的编程方法,在设计具体的系统过程中可以彻底的从复杂枯燥的编程工作中解放出来,而不需要用大量的精力去搭建实验系统设备,完成工程设计与应用的效率有了大大的提高。本文将虚拟仪器技术与电机信号检测技术相结合。研究了基于LabVIEW 的电机振动信号检测的方法,通过具体的应用测试,验证了该系统的实用性与高效性。
[1]张桐,陈国顺,王正林编著.精通LabVIEW 程序设计[M].北京:电子工业出版社,2008.
[2]杨乐平等.LabVIEW 高级程序设计[M].北京:清华大学出版社,2003.

