多臂井径测井有效通径算法研究

赵俊堂 （中石油长城钻探工程有限公司测井公司，辽宁 盘锦124011）

随着油田开发的逐步深人，油水井套管的损坏已成为一个比较突出的问题［1］。多臂井径成像测井是目前油水井套损检测中最重要的测井方法之一，可以完成套管检测中的多种测试，如油、套管变形、孔眼孔洞、裂缝、腐蚀、结垢、弯曲、断裂、射孔层段等［2］。目前，国内多臂井径仪器种类繁多，基本原理都大同小异，都实现了独立臂的测量，用于生产的主要有16臂、24臂、36臂、40臂、56臂和60臂等。但是多臂井径成像测井解释方法和软件起步晚，没有形成一个完整的体系，在解释中对原始数据做简单处理，主要以原始曲线作为解释依据，以最大、最小和平均值作为主要参考曲线，个别引入了椭变的相关数学曲线作为解释参考。仪器不居中、套管在发生弯曲和错断等情况时，井径测井获得的这些曲线并不能直观反映套管变形的真实形状，需要计算相关参数作为参考。截面的最大通径和有效通径是一个非常重要的参数，对采油厂进行套损作业改造非常重要，但目前还没有一个好的计算方法［1］。为此，笔者引入数学中计算多边形内切圆的方法，求多臂井径测井有效通径。

1 截面圆心、最大通径和有效通径计算

变形截面的最大通径是该截面能够通过最大圆形工具的直径，常规的方法取原始数据井径最小值作为最大通径是不合理的。变形截面的有效通径是指考虑变形井段通过最大圆形工具时该截面的最大通过直径，这2个参数对油水井套损的改造具有十分重要的指导意义。而有效通径的求取依赖于最大通径的求取，因此首先给出最大通径的求取方法。

通过计算多边形内切圆的方法来求取最大通径。首先确定多边形，设井径臂数为N，测得的各个井径数据分别为radi（i＝1，2，…，N），对井径数据进行去噪和插值计算，来达到计算精度。插值后的数据个数为M，各个数据值分别为di（i＝1，2，…，M），以（0，0）为圆心，以di为半径，以360／M 的角度绘制多边形，设多边形的各个顶点坐标为Pi（xi，yi）（见图1），则（xi，yi）的计算方法为：

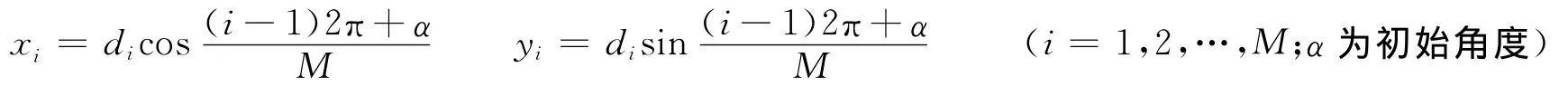
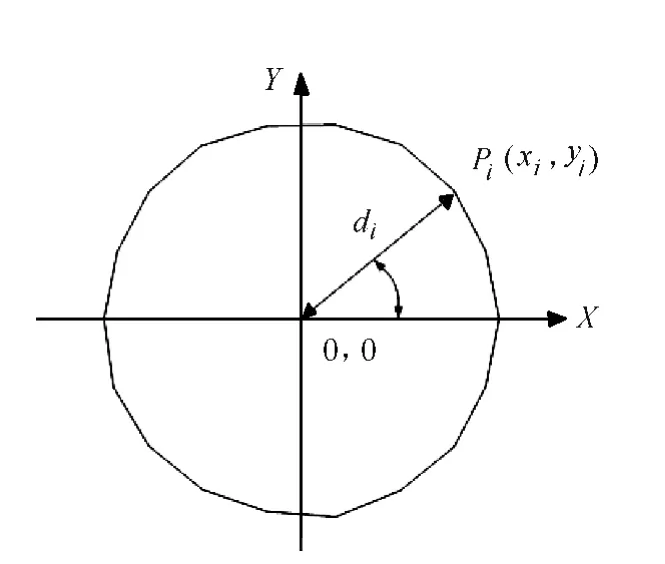
图1 最大通径计算示意图

该多边形的内切圆的计算步骤如下［3］：

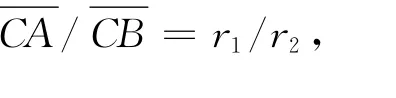
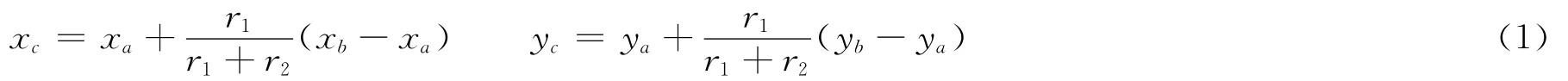
如初定圆心恰与A，B两点共线，则参考点取A点，即（xc，yc）＝（xa，ya）。利用参考点与初定圆心的位置关系，在CO 的延长线上取新的圆心位置0′（x′0，y′0），0′点坐标由式（2）计算：

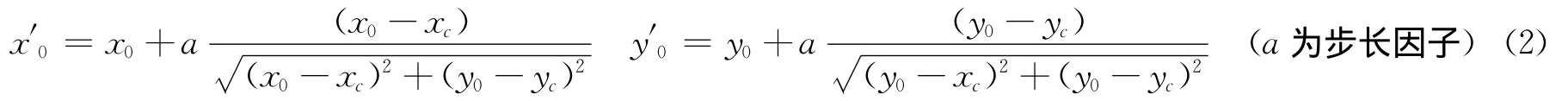
第2步：确定了新的圆心坐标0′后，计算新圆心至各边的最短距离，并将计算的最小距离r1与前次最小距离进行比较。若r1值增大，则继续第1步计算新的圆心坐标；若r1值减小，则应回到公式（2）重新计算新圆心坐标，但要调整补偿因子a，可取原a的一半或0.618倍。

重复以上2步，直到步长因子小到满足所给定的精度，则得到最大内切圆的圆心坐标（x0，y0）和最大内切圆半径ri。最大内切圆半径ri即为截面的最大通径L。

记0′到井径仪器轴心的距离为1，记该截面的最大通径为L，则该截面的有效通径为L－1。

2 软件实现

软件开发基于CifLog平台，利用该平台提供的二次开发接口，开发以上提出的通径计算方法模块 （见图2），编写人机交互解释界面，实现解释软件。开发的模块主要有预处理模块、优化计算模块、曲线计算模块、通经计算模块以及一些接口。

3 实际应用

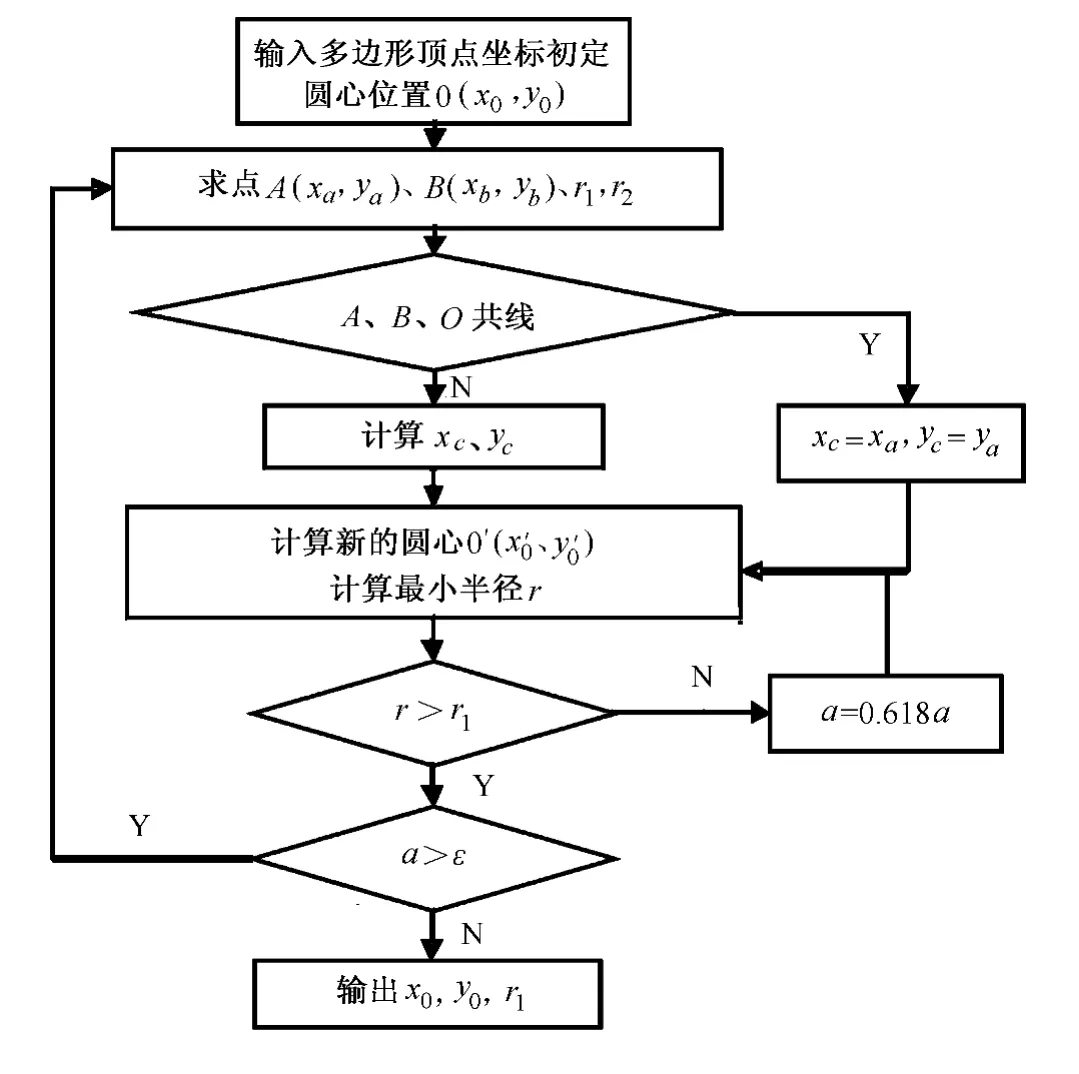
图2 通径计算程序设计图

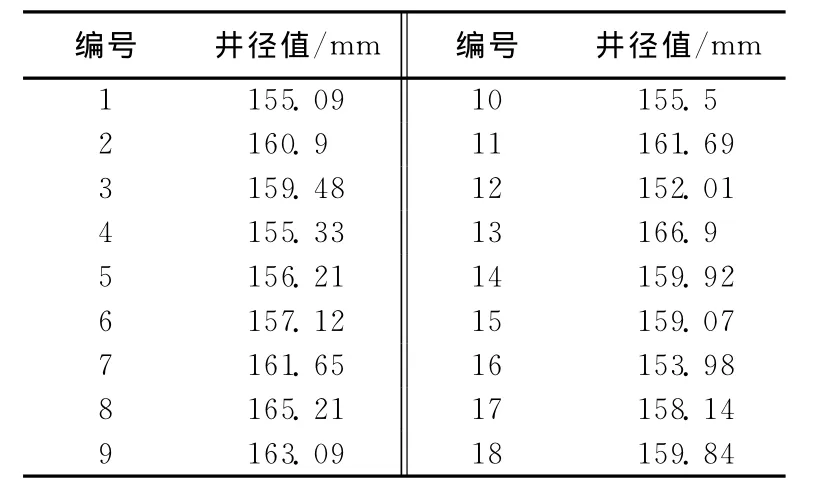
表1 JX井多臂井径测井849.71m处测井数据

图3 849.71m处截面图

表1是JX井十八臂井径测井数据中深度点849.71m处的18个井径数据。该井段套管外径177.8mm，内径159.4mm，实测数据显示最大内径166.90mm，最小内径为152.01mm。用新方法计算的通径相对圆心为 （－2.44，1.86），最大通径为153.66mm，有效通径为151.98mm。

图3为通过计算绘制的套管内径界面图，从计算的数据来看，计算的最大通径比最小内径大了1.65mm，通径圆心偏离仪器中心3.06mm。传统方法用最小内径作为最大通径的话，就会造成计算的有效通径偏小，从小影响油水井套损的改造设计和施工。

4 结 语

采用数学中步长因子自动控制搜索精度计算多边形最大内切圆的算法，计算多臂井径测井最大通径和有效通径，计算的结果可以从细节描述管柱的变形情况，为管柱的修补和下一步施工作业提供技术参数。

［1］周瑞芬 .最优化方法在多臂井径测井解释中的应用 ［J］.数学的实践与，2006，36（16）：127－129.

［2］王成荣，李文彬，秦小虹，等 .多臂井径成像测井技术 ［J］.石油仪器，2006，20（1）：44.

［3］郑梅生 .计算任意多边形最大内圆的一种算法 ［J］.机械设计与制造，2003（5）：84－85.