余期望系数与基尼系数比较研究

○罗文海 王 玖 韩春蕾

（滨州医学院 山东 烟台 264003）

国民收入分配不平等性是当前社会关注的焦点之一，而分析国民收入分配不平等性时则常用洛伦兹曲线和基尼系数。1905年，统计学家洛伦兹提出了著名的用以描述居民收入分配不均等性的方法，即洛伦兹曲线，但是该方法只能作定性描述，不能作定量描述。为了更好地反映国民收入分配的不均等性，1912年意大利经济学家基尼根据洛伦兹曲线计算出一个能反映国民收入分配不均等性的指标，称为基尼系数。此后，基尼系数逐渐成为国际上通用的衡量一个国家（地区）居民收入分配不均等性的统计指标。但是由于基尼系数还存在许多不足之处，如基尼系数计算比较繁杂和计算结果的精度不够高；对中间阶层收入的变化比对收入阶层两端的变化敏感；当用基尼系数分析相互联系的事物时，所得到的基尼系数彼此独立、缺乏可加性，影响了相互有联系事物的对比分析。因此，许多学者不断提出新的衡量国民收入分配不平等性的新方法，如我国学者于2003年提出了一种新的评价方法——余期望系数，此后许多人使用余期望系数进行国民收入分配不平等性的评价。本文试对基尼系数和余期望系数的意义、计算公式等方面进行比较，并作实证分析。

一、研究方法

洛伦兹曲线法是借助图形直观地表示收入分配不平等程度、非量化的定性指标。图1中横坐标是人口累计比重，纵坐标是收入累计比重，根据洛伦兹曲线与绝对平均线的位置关系来判断收入分配的不平等程度。所以，在应用时存在限制条件，即当两洛伦兹曲线不相交时才可用于比较，而相交时则不能进行收入分配的不平等性比较。洛伦兹曲线的位置越低，收入分配的不平等性越严重。

洛伦兹曲线和绝对平均线（对角线）之间的月牙形面积S，可以用来表示实际收入分配不平等性。这块月牙形面积越大，洛伦兹曲线弯曲度越大，说明收入差距越大，贫富两极分化越严重。反之，这块月牙形面积越小，洛伦兹曲线越平缓，说明社会收入分配差距越小，贫富两极分化越不明显。根据月牙形面积S与绝对平均线右下方的三角形面积P，可以计算基尼系数，见式（1）（几何法）。

为计算方便，基尼系数G的数值常按式（2）（基尼平均差法）计算：

式（2）中n是人口等分组的个数，yi是人口等分组收入的均值。

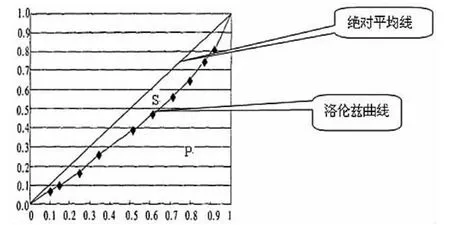
图1 洛伦兹曲线

表1 2005—2008年全国城镇居民收入分配数据

余期望系数是国内学者近些年来新提出的收入分配不平等性的测量方法，其基本思想是从信息量角度出发而设计出来的指标。设p是事件B发生的概率P（B）=p。对于不容易发生的事件，我们越要想全面了解，需要的信息量也就越大，因此对于事件B发生所需的信息量假定为p的减函数log（1/p）。假如有n个事件，发生的概率分别为p1、p2…pn。从概率论的期望公式出发，期望信息量则可定义为：

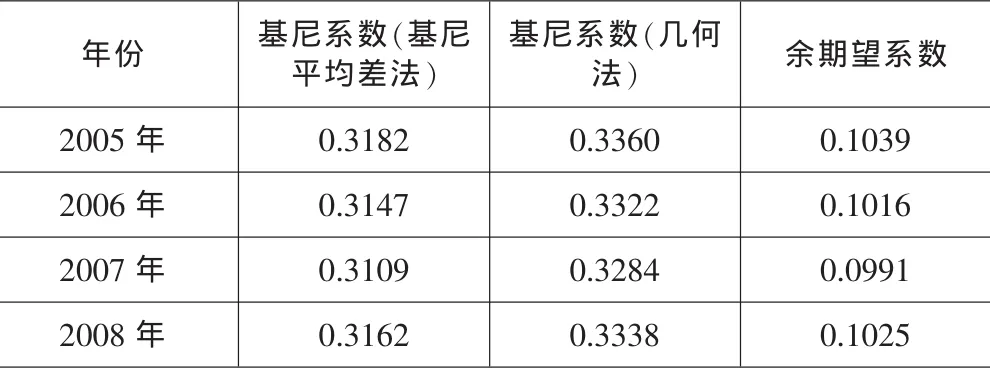
表2 全国城镇居民收入分配的基尼系数和余期望系数分析

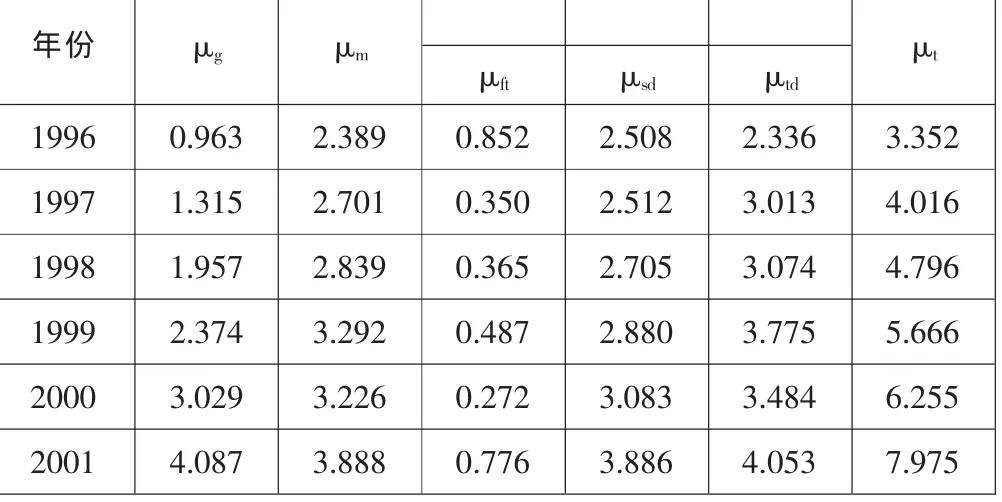
表3 江苏省三个产业在岗职工年平均工资余期望系数单位：%

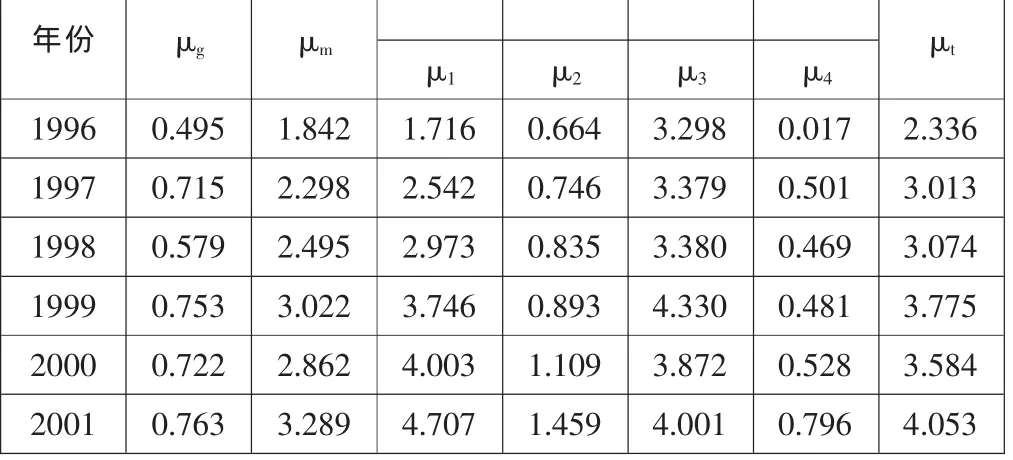
表4 江苏省第三产业在岗职工年平均工资余期望系数单位：%

概率 p1，p2，…，pn的值越接近，期望信息量E就越大。如果p1=p2=…=pn=1/n，则E达到最大值logn。于是可定义余期望系数：

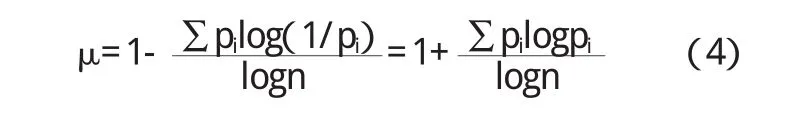
如果把pi视为第i个单位所占的收入份额，即pi=Wi/ΣWi，（Wi为第i个单位的收入，i=1，2，…，n），则余期望系数 μ 可以测度收入分配的差异性。该系数愈靠近0，表明单位之间收入差异愈小；愈靠近1，表明单位之间收入差异愈大。

与基尼系数相比，由于余期望系数的数学含义及表达式简单明了，不涉及不规则图形面积的计算，因此其计算精度能得到保证，根据余期望系数作出的分析判断具有较高的可信度。

二、研究资料与结果

本文选取中国统计年鉴中2005—2008年的全国城镇居民收入分组数据作基尼系数和余期望系数计算结果的比较。在计算国民收入分配不平等性时，国际上常用收入5等份分组数据进行计算，而中国统计年鉴给出的数据为7分组不等距分组数据，因此先将数据转换为5等份分组数据，见表1。根据上述5等份分组数据，分别计算基尼系数（几何法，式（1））、基尼系数（基尼平均差法，式（2））和余期望系数（式（4）），计算结果如表2所示。

由表2可知，根据2005—2008年全国城镇居民收入分配数据，由几何法计算的基尼系数比由基尼平均差法计算的基尼系数要略微大一些，平均大5.6%。余期望系数的计算结果明显比由上述两种方法计算的基尼系数要小，同一资料计算的余期望系数的数值约为基尼系数的1/3，差别明显。

此外，基尼系数的一个不足之处是缺乏可加性，而余期望系数与之不同具有可加性，下面以表3、表4资料为例说明其可加性。

表4中，μt为总余期望系数，μg为单位间余期望系数，μm为单位内余期望系数，μ1、μ2、μ3、μ4、μft、μsd、μtd为组内（单位内）亚单位的余期望系数，μ1、μ2、μ3、μ4为第三产业包含的 4个亚单位（4个层次）的余期望系数，4个层次分别包含不同的内容。μft、μsd、μtd分别为第一、第二、第三产业的余期望系数。余期望系数的可加性是指表3、表4的μt是μg和μm之和，如表3中的1999年μg（2.374）+μm（3.292）=μt（5.666）。μm为组内亚单位的余期望系数的加权和，权数按亚单位人数比重计算。但是经过细致的研究发现，根据表3、表4依据的江苏省统计年鉴的数据计算出的组内亚单位的余期望系数的加权和与表3、表4的μm值有差别，以1999年的有关数据为例，详细的比较数据，见表5。

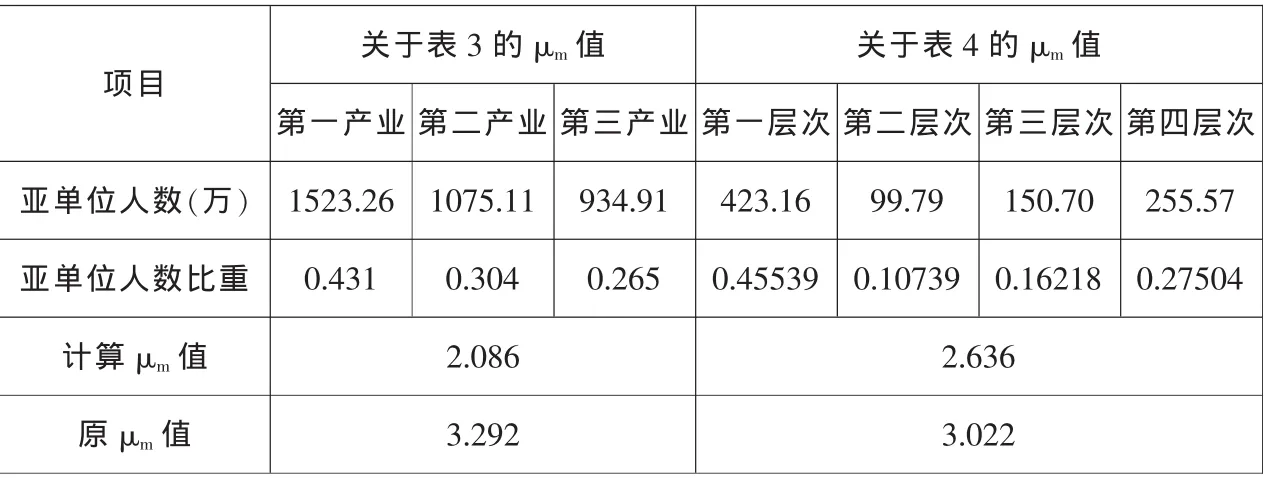
表5 1999年数据计算的单位内余期望系数μm值比较

三、结论

虽然国民收入分配公平性研究是一个常见的重要课题，但是现有的统计分析方法不同程度地存在着这样或那样的问题，因此科技工作者不断提出一些新的分析方法。余期望系数是近些年来由我国科技工作者提出的新方法，之后许多人开始采用余期望系数进行国民收入分配不平等性等分析。

表2显示用同一资料按几何法计算的基尼系数和按基尼平均差法计算的基尼系数的数值略有差别，这与许多文献的结论相似。表2显示的全国城镇居民收入分配的基尼系数的结果与许多文献结果一致。全国城镇居民收入分配的余期望系数的数值未见文献报道，但是少数文献涉及到全国部分地区居民收入分配的余期望系数的数值，多篇报道的余期望系数的数值与表2显示的全国城镇居民收入分配的余期望系数的结果比较一致。表2显示用同一资料计算的余期望系数的数值比基尼系数数值明显偏小，约为1/3。但是二者的变化规律相同，如在2005—2008年的四年中，这二者的数值均是2007年最低、2005年最高。余期望系数和基尼系数的这种关系可以为其他人讨论余期望系数和基尼系数的数量关系提供参考，例如可以根据目前广泛使用的基尼系数的数值来粗略推算相应的余期望系数。

[1]王海港：收入分配不平等的概念及其度量综述[J].阴山学刊，2005，18（5）.

[2]解火亘、莫旋：论不平等程度度量的统计方法[J].长春师范学院学报（自然科学版），2005，24（6）.

[3]尚卫平：一种反映收入差异程度的新指标——余期望系数[J].统计研究，2004（1）.

[4]姚智谋：三次产业在岗职工工资收入差异程度研究——以南京市为例的实证分析[J].南京财经大学学报，2006（6）.

[5]彭娜、王运松、聂思举、徐世英：我国民族地区城乡收入差异程度的实证分析[J].中央民族大学学报（自然科学版），2011，20（4）.

[6]王祖祥：收入不平等程度的度量方法研究[J].经济评论，2001（5）.

[7]张云霞、李梅、刘中雨、侯冬梅：山西省卫生资源配置公平性研究——基于洛伦兹曲线与基尼系数方法[J].卫生经济研究，2011（9）.

[8]钱敏泽：中国现行统计方法基尼系数的推算及结果[J].经济理论与经济管理，2002（11）.

[9]陈建东、戴岱、冯瑛：居民收入样本分组数与基尼系数测算的关系探讨[J].统计与决策，2011（15）.

[10]张新春、尚卫平：我国农村居民家庭收入差异与影响因素分析[J].科技情报开发与经济，2007，17（24）.

[11]尚卫平：我国三次产业在岗职工工资收入差异程度研究—以江苏省为例的实证分析[J].财经研究，2003，29（11）.

[12]李瑞、杜宝苍：基尼系数求解方法的简要描述[J].经济研究导刊，2012（8）.

[13]瞿晶、姚先国：城镇居民收入不平等分解研究[J].统计研究，2011，28（11）.

[14]田卫民：中国基尼系数计算及其变动趋势分析[J].人文杂志，2012（2）.

[15]朱红菠、彭莉莎、申付亮：四川省城镇居民可支配收入公平度的测量与分析[J].数据，2009，18（6）.