船舶电力系统谐波检测

管 旭

(渤海船舶职业学院电气工程系，辽宁省葫芦岛125005)

0 引言

20世纪80年代中期以来，主要归功于功率半导体器件的飞速发展，使电力电子技术快速兴起。采用功率半导体器件实现变频装置的作用就是变流。但是在变流过程中，使用了电力半导体器件的开关特性，其输入和输出侧电压和电流都会出现波形畸变现象，产生丰富的谐波[1]。船舶上大量应用电力电子技术给船舶电网带来了谐波问题，严重影响电源质量，国内外都有因为谐波问题而引发的重大船舶事故。船舶电力系统用电设备的谐波标准日益提高，而现阶段直流传动系统和交流传动系统都会给船舶电网注入大量的谐波，因此船舶电力系统首先要解决的就是谐波问题。

谐波问题涉及面很广，其中包括谐波抑制、畸变波形的分析方法、谐波源分析、电网谐波潮流计算、谐波限制标准以及谐波测量等。谐波检测是谐波问题的一个重要分支[2]。

本文在对现存谐波检测方法及相关技术进行分析和总结的基础上，进行相应的仿真研究，验证其有效性。

1 谐波的主要检测方法

谐波检测是研究分析谐波问题的出发点和主要依据。谐波检测方法按原理可分为：模拟滤波器；基于傅立叶变换的谐波检测法；基于瞬时无功功率理论的谐波检测法；基于神经网络的谐波检测法；基于小波分析的谐波检测法。谐波检测（包括对所有谐波源用户的设备投运时的测量）主要是鉴定实际电力系统及谐波源用户的谐波水平是否符合标准，以确保设备投运后船舶电力系统和设备的安全及经济运行。

1.1 基于模拟滤波器的谐波检测

模拟滤波器谐波检测方法的优点是：能滤除一些固有频率的谐波，电路结构简单，造价低，品质因数易于控制等。该方法的缺点有：不仅实现电路的滤波中心频率 f1,f2…,fn的元件受外界环境的影响很大，很难获得理想的幅频特性及相频特性，而且只能对少量谐波进行检测且检测精度较低。因为存在这些缺点，所以目前基本上不用这种早期的谐波检测方法。

1.2 基于傅立叶变换的谐波检测

目前基于傅立叶变换的谐波测量基本采用由离散傅立叶变换过渡到快速傅立叶变换算法进行检测。这种测量方法对低频（稳态）谐波检测精度较高，使用也比较方便，目前应用较为广泛。但其缺点在于检测时间长，检测结果实时性较差，而且会产生频谱泄漏效应和栅栏效应，使计算出的信号参数尤其是相位的误差很大[3]。为了降低频谱泄漏效应和栅栏效应产生的影响，人们想出了多种方法。例如：加窗差值算法、双峰谱线修正算法、利用数字式锁相器(DPLL)使信号频率和采样频率同步方法，其中自适应采样算法根据信号频率实时调整采样频率，确定下一采样时间。该算法不仅频谱泄漏的影响较小、实时性较好，而且精度也比较高，与固定采样率算法相比，基本不需增加计算量。

1.3 基于瞬时无功功率理论的谐波检测

1983年日本学者赤木泰文提出了瞬时无功功率理论。根据该理论，瞬时有功功率p和瞬时无功功率q中都含有直流分量和交流分量，从中可得被检测电流的基波分量，将总电流减去基波分量可得相应的谐波电流。该理论使得电力有源滤波理论由实验室的理论研究走向实际应用。该方法只适用于三相电压正弦、对称情况下的三相电路谐波和基波无功电流的检测[4]。对于单相电路，必须首先构建三相电路才能进行谐波检测，这种方法的优点是当电网电压对称且无畸变时，各电流分量的测量电路比较简单，并且延时小。但所需硬件多，花费大[5,6]。在目前条件下，采用这种方法相比之下是得不偿失的。

1.4 基于神经网络的谐波检测

研究神经网络的目的有两个：一是探索和模拟人的感觉、思维和行为的规律，设计具有人类智能的计算机系统；二是探讨人脑的智能活动，用物化的智能来考察和研究人脑智能的物理过程及其规律。目前对神经网络的研究取得了丰硕成果，己应用于许多重要领域，如模式识别与图象处理、控制与优化、预测与管理、通信等。

1.5 基于小波变换的谐波检测

小波分析(Wavelet Analysis)是一种新兴的数学分支，它是泛函数、Fourier分析、调和分析、数值分析的最完美的结晶。它被认为是继Fourier分析之后的又一有效的时频分析方法。小波变换与Fourier变换相比，是一个时间和频域的局域变换因而能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，解决了 Fourier变换不能解决的许多困难问题。由于小波变换克服了傅里叶变换在频域完全局部性而在时域完全无局部性的缺点，实现了理论上的全面性，广泛应用于信号处理、图象处理与分析等领域。

2 利用小波多分辨率分析对船舶电网谐波进行检测

小波多分辨率分析在对非稳态成分谐波进行检测时，有其独特的优势。由于船舶工作条件的复杂性等因素，导致船舶电网谐波问题比陆上大电网更为突出，而且多为非稳态谐波，所以适用小波多分辨率变换对其进行分析。本节将使用MATLAB平台的小波工具箱对船舶电网现场采集的谐波进行小波多分辨率分析仿真检测。

一般来讲，移动船舶电站中高次谐波幅值会随频率升高而降低，基波频率为工频50 Hz或60 Hz。根据香农采样定理，把采样频率设定在6 kHz，则最高次的检测谐波为3000 Hz（即50次谐波）。小波多分辨率分析谐波检测的原始信号来自现场船舶变压器中电压波形，采样点取为

2000，试验中采集到的数据经过通讯线路传出到电脑中，经过MATLAB得到如图1所示的信号波形图。

测试环境：两台柴油发电机组并网发电。1#机组和2#机组的输出电流均为1100 A，有功功率分别为736 kW、735 kW，无功功率分别为1270 kVar、1260 kVar。电压总畸变率THDu=46%。

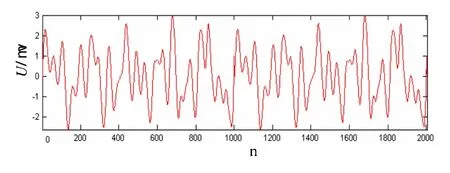
图1 由实验装置采集到的某船舶变压器现场信号

小波基的选择在利用小波变换进行系统谐波检测中十分重要。本节根据小波基的选择条件，选用的小波基为DB2[7]。图2所示是船舶现场信号利用小波多分辨率分析分离后各个频段的重构波形。

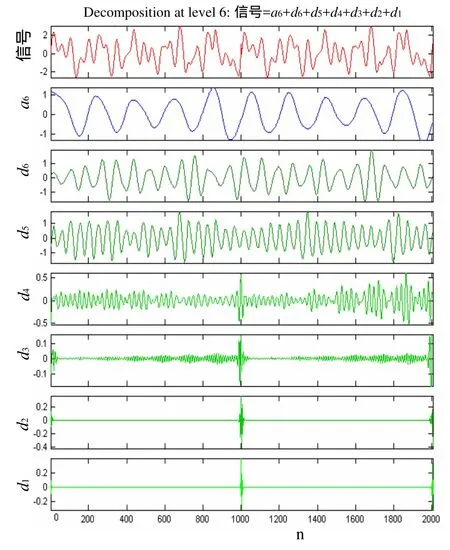
图2 尺度为6的db2小波分解

从图中可以很清楚地看到，尺度1、2、3中的局放信号清晰，所以将尺度1、2、3下分解的信号重构，得出了如图3的局放脉冲谐波信号。

以上是利用小波多分辨率理论，通过MATLAB仿真程序对某船舶正常作业时的对某变压器处进行现场检测。检测结果表明: 小波多分辨率算法在基波幅值相对稳定的情况下，可以比较准确地分离出船舶电力系统的高次谐波信号。

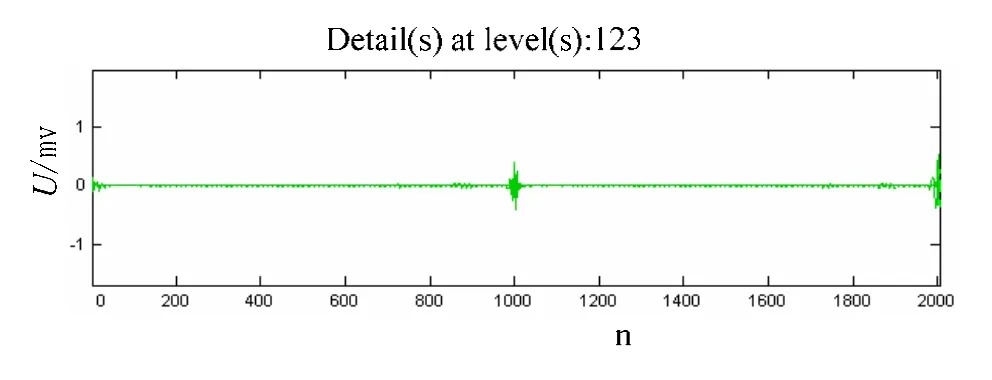
图3 经测量得到的谐波信号

3 总结

本文对现存的谐波检测方法详加分析，并在此基础上用小波多分辨率理论，通过 MATLAB仿真程序对某船舶进行现场检测，结果证明：小波多分辨率理论可以对船舶电力系统谐波问题进行比较准确的分析。

：

[1]肖湘宁. 电能质量分析与控制. 北京: 中国电力出版社, 2004.

[2]Yang Junzhe, Yu Chishan, Liu Chiwen. A new method for power signal harmonic analysis. In: IEEE Transactions on Power Delivery, 2005, 20(2): 1235-1239.

[3]唐岩. 电力系统谐波测量方法简述. 青海大学学报(自然科学版), 2005, 2 (1): 21-26.

[4]刘开培, 张俊敏, 陈艳慧. 基于重采样的三相谐波检测瞬时无功功率法.电力系统自动化, 2003, 27(12):45-47.

[5]王兆安, 李民, 卓放. 三相电路瞬时无功功率理论的研究.电工技术学报, 1992, 7(8): 55-59.

[6]张桂斌, 徐政, 王广柱. 基于空间矢量的基波正序、负序分量谐波分量的实时检测方法.中国电机工程学报, 2001, 21(10): 1-5.

[7]飞思科技产品研发中心. 小波分析理论与MATLAB7实现. 北京: 电子工业出版社, 2005.