基于卡尔曼滤波的多传感器跟踪融合算法

王永安，何光进， 刘毅

（1. 海军91880部队，山东胶州 266300；2. 海军工程大学兵器工程系，武汉 430033）

0 引言

多传感器信息融合是指对来自多个传感器的数据进行多级别、多方面、多层次的处理，从而产生新的有意义的信息，而这种信息是单一传感器无法获得的。

卡尔曼滤波器是对运动目标进行跟踪和预测的良好方法，它具有模型简单、数据存储量小的特点，特别适用于航天、航空、航海、系统工程等多种领域。

1 卡尔曼滤波的基本方程

一般离散线性系统的卡尔曼模型由状态方程、观测方程及一步预测及更新方程组成，具体如下[1]：

状态方程：

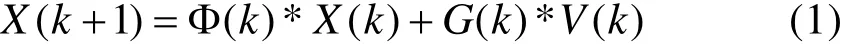
观测方程：

上式中，X( k)为系统在k时刻的状态向量；Φ (k)为状态转移矩阵；V( k)和G( k)分别为过程噪声和过程噪声控制矩阵，V( k)是具有零均值和正定协方差矩阵 Q的高斯过程噪声。H( k)为观测矩阵，W( k)为观测噪声，具有零均值和正定协方差矩阵R。

误差协方差更新方程：

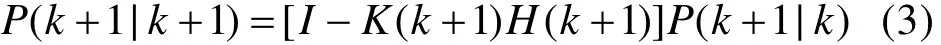
滤波器状态更新方程：

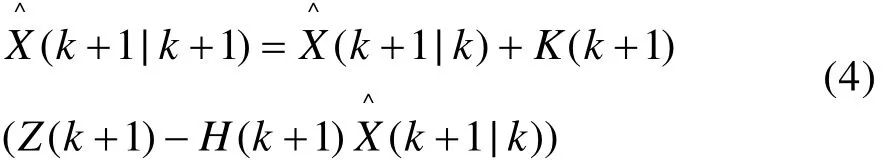
若知道了滤波器的状态初始值 x(0|0)和误差协方差初始值 p(0|0)，就可以通过上式对目标的运动状态进行预测了。

2 数据融合算法的分类

数据融合算法主要分为集中式、分布式和混合式，分别如图1、图2和图3所示。

集中式和分布式是多传感器信息融合跟踪系统中最具根本性和重要性的两种结构，下面分别对它们的算法及估计性能做一分析。

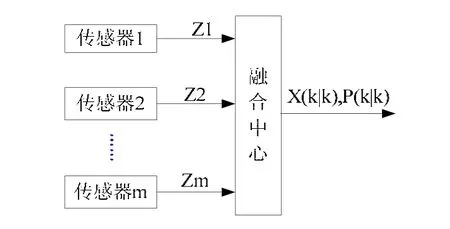
图1 集中式融合模式

图2 分布式融合模式

图3 混合式融合模式

3 集中式信息融合算法

各个传感器将观测矩阵送至融合中心，融合中心综合各个传感器的观测数据做出判断，给出最优的结果。因信息损失小，理论上它可以获得最优的融合性能，但是它对资源（通信带宽、融合合中心的处理能力等）要求较高。

根据对观测数据的处理方式和观测数据的实时性，集中式融合可分为以下四类：扩维融合、加权融合、同步序贯融合和异步序贯融合。下面通过仿真对前三种融合算法进行分析比较。

3.1 扩维融合

在扩维融合方式中，融合中心将各传感器将送来的观测数据放在同一个矩阵，其模型为[2]：

融合中心的状态方程：

融合中心的观测方程：

其中：

噪声协方差阵：

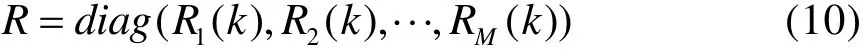
其中： R1( k),R2( k ),· ··,RM(k)分别为M个传感器的观测噪声协方差矩阵。

下面针对文献[3]一个实际系统对集中式融合前后的性能作一分析，不同的是我们将传感器的数据推广到三个。

系统的模型为：

状态方程：

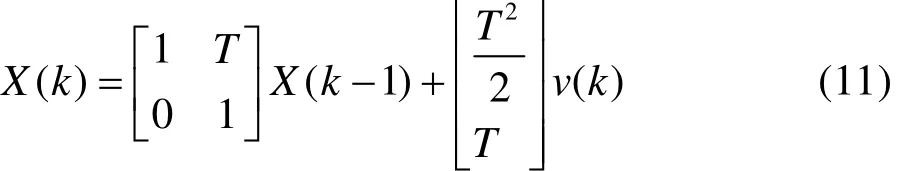
每个传感器的观测方程：

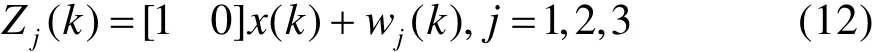
其中：采样间隔T=1 s，v( k)， wj( k)分别为过程噪 声 和 观 测 噪 声 ， 满 足 ： E( v( k ))= 0,E( v( k)v( k)')=q、 E( wj( k ))= 0,j= 1,2,3、E( wj( k)wj( k )')=Rj、E( wi( k)wj( k )')= 0,i≠ j。另外，为了简化分析，我们也假设v( k)、wj( k)和状态初始值x(0|0)均相互独立。

假设运动目标在k=0时刻位于x-y坐标系的原点并前沿x轴正向以10 m/s的速度运动。对系统的仿真结果如图4所示，仿真中采用了100次的蒙特卡罗仿真（下同）。

3.2 加权融合

集中式数据融合的另一种结构是在局部节点对观测数据进行加权平均，它要求所有传感器的观测矩阵是相同维数的（至少存在公共向量，通过补零来实现维数相同）。加权值为各个观测值的噪声协方差的逆。若每个传感器观测值为 Zi( k)，观测矩阵为 Hi( k)，观测噪声协方差为Ri，则它的加权模型为[4]：

加权后的观测值：

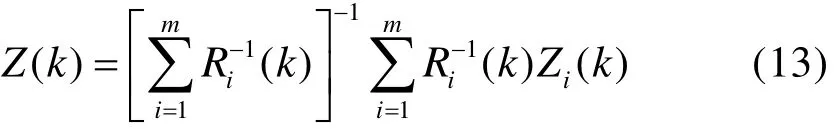
加权后的观测向量：

加权后的观测噪声协方差：

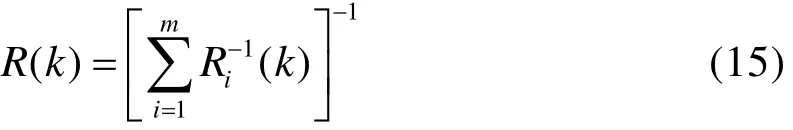
图4 扩维融合前后的位置和速度误差协方差比较

加权融合是在最小均方意义上对观测数据进行处理，同扩维融合方式相比，它对资源的要求减少很多，具有明显的优点[4]。

仍然用上一个例子对加权融合的性能进行仿真，仿真的结果如图5所示。通过比较可以看出，加权融合和扩维融合具有相同的预测误差，这说明在一定的条件下，加权融合和扩维融合可以获得相同的估计性能，但可以节省很多资源和减少计算复杂度。

3.3 同步序贯融合

对于融合中心来说，各个传感器的观测值可以看作是一个具有零预测时间的新测量[1]，融合中心将某一可靠性较高的传感器作为主传感器，先用主传感器的数据对融合中心的状态进行预测，然后用其它传感器的数据依次更新融合中心的状态，得到融合后的状态矢量。

同步序贯融合的一般步骤为[5]：

1) 用( k| k)和P( k| k)计算出一步预测值( k + 1|k )和P( k+ 1|k)；

2) 用主传感器的观测数据Z( k)对融合中心的 状 态 进 行 更 新 ， 得 到( k + 1|k + 1)和P( k + 1|k + 1)。

3) 令( k + 1|k)=( k + 1|k + 1)，P( k + 1|k)= P( k + 1|k + 1)，即把上一传感器的估计结果作为下一传感器的一步预测估计。用下一传感器的观测数据更新融合中心的状态。

4）重复2)和3)，完成对整个系统的更新。

用此方法对式(11)和(12)所表示的系统进行仿真，结果如图6所示。可以看出，融合后的位置和速度误差协方差和单个传感器的融合性能相比并没有得到很好的改善，这是因为每个传感器都基于自己的判断对目标状态进行更新。

图5 加权融合前后的位置和速度误差协方差比较

图6 同步序贯融合前后的位置与速度误差协方差比较

4 分布式信息融合算法

和集中式融合算法不同，分布式融合算法不是将每个传感器的观测值送入融合中心，而是局部节点先对目标的运动状态作一预测，然后将预测轨迹送入融合中心，和集中式相比，它传输的数据量较少且可靠性和可扩展性较高，成为研究的重点[6]。

分布式信息融合算法分以下几种：直接式、同步序贯式、异步序贯式、反馈式、分层式。下面通过仿真对其中两种算法进行分析比较。

4.1 直接式分布融合算法

同直接式集中融合算法类似，不同的是每次送往融合中心不是各传感器（组）的观测值，而是已经进行处理后的目标状态：X( k| k)和P( k| k)。算法如下[2]：

一步预测方程：

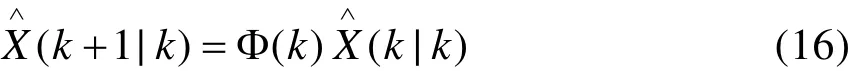
一步协方差预测方程：

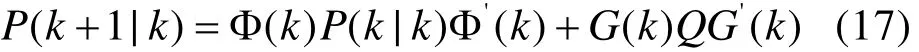
误差协方差更新方程：

状态更新方程为：

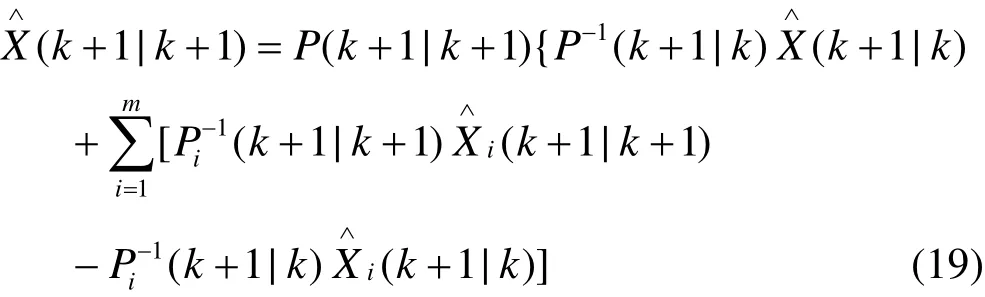
用式(11)和(12)所表示的系统进行仿真，结果如图7所示。从图中可以看出融合性能和集中式的融合性能一致。

图7 分布式直接融合前后的位置与速度误差协方差比较

4.2 异步序贯式分布融合算法

同异步序贯集中式算法类似，它可以通过增加传感器的数量来提高对目标的跟踪精度，下面对它的融合效果作一仿真。仿真结果如图8所示。从图中可以看出，对速度和位置的估计达到了预期的目标。

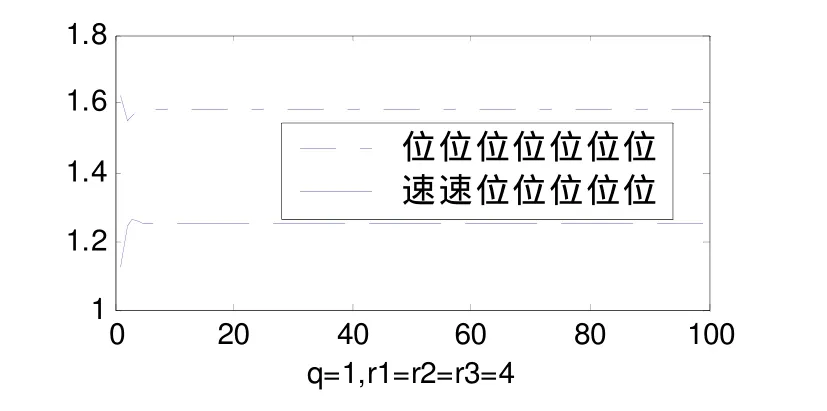
图8 异步序贯分布融合后的位置和速度的误差协方差估计

5 总结

本文总结了基于卡尔曼滤波技术的各种算法，集中式融合算法具有最优的估计性能但是对资源的要求也最高。分布式融合算法可以节省计算量和通信带宽，在一定条件下也可以达到对目标的最优估计。各种融合算法在不同的背景下都有实际的工程应用价值，对它们的研究将有助于理解和改进现有的各种融合算法，减少目标的不确定性，提高跟踪精度。

：

[1]. 何友, 王国宏等. 多传感器信息融合及应用[M]. 北京: 电子工业出版社, 2007.

[2]. Sumedh Puranik, Thomas C. Jannett. A comparison of the tracking performance of some distribute multi-sensor data fusion algorithms based on Kalman filter methods[J]. IEEE, 2003: 455-459.

[3]. Chang,K.C., Saha, R. K., and Bar-Shalom, Y.. On optimal track-to-track fusion. IEEE Transactions on Aerospace and Electronic Systems, 1997,33(4):1271-1276.

[4]. X.R.Li. Comparison of two measurement fusion methods for Kalman –filter-based multisensor data fusion[J]. IEEE Transactions on Aerospace and Electronic Systems,2001(37):273-280.

[5]. 文成林, 吕冰, 葛泉波. 一种基于分布式滤波的数据融合算法[J]. 电子学报, 2004(32), 1264-1267.

[6]. 李涛, 王宝树, 乔向东. 带反馈多传感器分层融合算法性能研究[J]. 宇航学报, 2005(26)732-736.

[7]. 朴美善, 林象平. 基于分层融合的快速融合系统[C].中国造船工程学会电子技术学术委员会年会论文集,2001: 93-96