基于Kalman滤波的多传感器信息融合研究

刘洲洲

（西安航空学院 陕西 西安 710077）

多传感器信息融合的基本原理是充分地利用多个传感器资源，通过对多传感器观测信息合理使用，把各种传感器在空间和时间上的互补与冗余信息依据某种优化准则组合起来，从而对观测环境进行一致的描述和解释。基于各传感器分离观测信息，通过对信息的优化组合导出更多信息，利用多个传感器共同或联合操作的优势，提高整个传感器系统的有效性[1]。

1 多传感器信息融合理论

融合方法研究的内容是与数据融合有关的算法[2]。信息融合算法，一般可以分为经典和现代方法。经典方法包括加权平均法、最小二乘法、极大似然估计、卡尔曼滤波、D-S证据理论和贝叶斯估计等。现代方法包括模糊逻辑、人工神经网络、遗传算法、模糊积分理论等。数据融合过程如图1所示。

1.1 卡尔曼滤波（KF）

卡尔曼滤波用测量模型的统计特性，递推决定统计意义下最优融合数据合计。KF分为分散卡尔曼滤波（DKF）和扩展卡尔曼滤波（EKF）。DKF可实现多传感器数据融合完全分散化，其优点是，单个传感器节点失效不会导致整个系统失效[3]。而EKF的优点是可有效克服数据处理不稳定性或系统模型线性程度的误差对融合过程产生的影响。

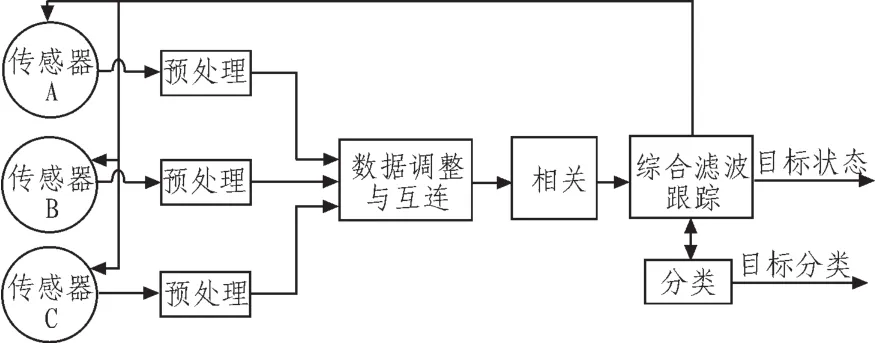
图1 数据融合过程Fig.1 Data fusion process

1.2 人工神经网络法

人工神经网络法[4]通过模仿人脑的结构和工作原理，设计和建立相应的机器和模型并完成一定的智能任务。神经网络多传感器信息融合的实现，分3个重要步骤：

1）根据智能系统要求及传感器信息融合的形式，选择其拓扑结构；

2）各传感器的输入信息综合处理为一总体输入函数，并将此函数映射定义为相关单元的映射函数，通过神经网络与环境的交互作用把环境的统计规律反映到网络本身结构；

3）对传感器输出信息进行学习、理解，确定权值的分配，完成知识获取信息融合，进而对输入模式做出解释，将输入数据向量转换成高层逻辑概念。

1.3 D-S推理

假设F为所有可能证据所构成的有限集，Ai为集合F中的某个元素（证据）。 引入信任函数 B（f）∈[0，1]，它表示每个证据的信任程度：B（F）=1，B（φ）=0。

引入基础概率分配函数 m（f）∈[0，1]，满足 m（Φ）=0 和（A）=1，与之相对应的信任函数：

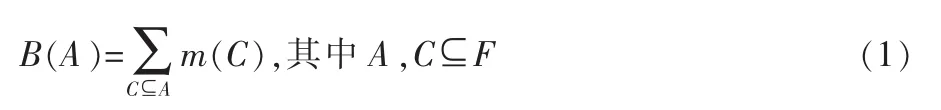
1.4 Bayes估计

Bayes[5]估计是融合静态环境中多传感器低层数据的一种常用方法，其信息描述为概率分布，适用于具有可加高斯噪声的不确定性信息。假定完成任务所需的有关环境的特征物用向量f表示，通过传感器获得的数据信息用向量d来表示，d和f都可看作是随机向量。信息融合的任务就是由数据d推导和估计环境f。假设p（f，d）为随机向量f和d的联合概率分布密度函数，则

p（f|d）表示在已知d的条件下，f关于d的条件概率密度函数；p（d|f）表示在已知f的条件下，d关于 f的条件概率密度函数；p（d）和p（f）分别表示d和f的边缘分布密度函数。已知 d 时，要推断 f，只须掌握 p（f|d）即可，即

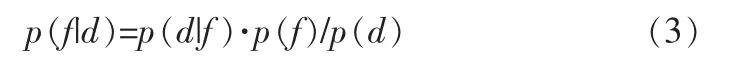
上式为概率论中的Bayes公式。

信息融合通过数据信息d做出对环境f的推断，即求解p（f|d）。 由 Bayes公式知，只须知道 p（f|d）和 p（f）即可。 因为 p（d）可看作是使 p（f|d）·p（f）成为概率密度函数的归一化常数，p（d|f）是在已知客观环境变量f的情况下，传感器得到的d关于f的条件密度。当环境情况和传感器性能已知时，p（f|d）由决定环境和传感器原理的物理规律完全确定。p（f）可通过先验知识的获取和积累，逐步逼近得到。

2 基于Kalman滤波的多传感器融合仿真

卡尔曼滤波处理[6]的基本思路是:对于运动目标，由描述目标运动模型的线性动态方程，在当前滤波估值的基础上预测下一时刻的目标状态，并将这一预测值与下一时刻状态观测值加权平均，获得下一时刻的滤波估值，由此实现连续、实时的、递归滤波。

动态系统的状态方程和量测方程，它们分别为[4]：

在状态方程和量测方程中，一般Ak与Ck是已知的，yk是量测的数据是已知的。式（1）和式（2）得到xk与yk分别用表示，则有，

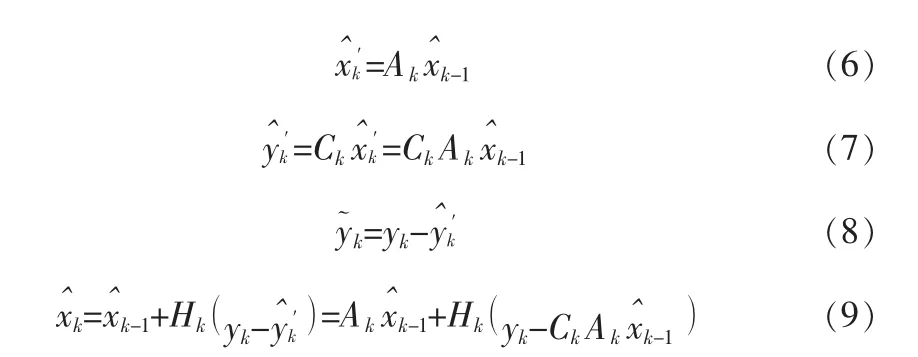
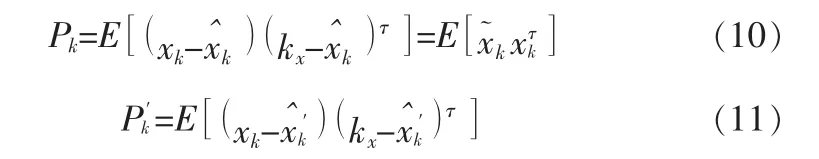
得到卡尔曼一步递推公式：

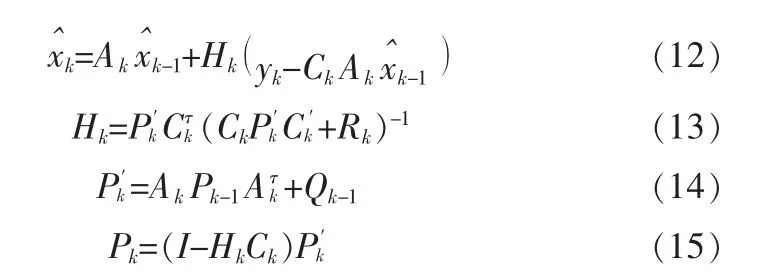
基于卡尔曼滤波理论，设置初始状态，在目标跟踪环境下，基于Kalman滤波的多传感器仿真如图示2所示。

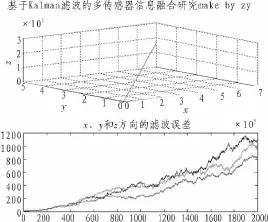
图2 基于Kalman滤波的多传感器仿真Fig.2 Based on Kalman filtering multisensor simulation

其中最上边曲线的表示X方向的滤波误差，中间的曲线则代表了Y方向的滤波误差，Z方向的滤波误差由最下面的曲线表示。

3 结 论

多传感器信息融合将来自不同途径，不同时间，不同空间的传感器信息协调成统一的特征表达式，以完成对某一对象和环境特征的描述。文中搜集、整理和总结今年来国内外在信息融合领域的最新研究成果和最新进展，借鉴其相关的经验。运用MATLAB对卡尔曼滤波进行仿真，验证了算法的可行性。

[1]王军，苏剑波，席裕庚.多传感器集成与融合概述[J].机器人，2011，23（2）：55-57.WANG Jun，SU Jian-bo，XI Yu-geng.Overview of multisensor integration and fusion of[J].Robot，2011，23 （2）:55-57.

[2]罗跃纲，陈长征.基于信息融合的集成小波神经网络故障诊断[J].东北大学学报：自然科学版，2012，23（8）:802-805.LUO Yue-gang，CHEN Chang-zheng.Information fusion based on integrated wavelet neural network fault diagnosis[J].Journal of Northeastern University：Natural Science Edition，2002，23（8）:802-805.

[3]袁南儿，杨东勇，林毅.多传感器信息融合及其在工业控制中的应用[J].浙江工业大学学报，1999，27（4）:77-79.YUAN Nan-er，YANG Dong-yong，LIN Yi.The multi sensor information fusion and its application in industrial control[J].Journal of Zhejiang University of Technology，1999，27 （4）:77-79.

[4]王华奎，张立毅.数字信号处理及应用[M].太原：太原理工大学出版社，2003.

[5]李国勇，谢克明.控制系统数字仿真与CAD[M].北京:电子工业出版社，2003.

[6]彭冬亮，文成林，薛安克.多传感器多源信息融合理论及应用[M].北京:科学出版社，2010.