基于状态空间的Buck型变换器数字电压控制

李 峰

（中国电子科技集团公司20所，西安710068）

0 引 言

利用经典控制理论进行Buck型变换器的数字控制器设计时，需要先完成控制器的连续域（s域）设计，然后再将其转换成离散域（z域）的差分方程以实施数字控制［1］，这导致数字控制系数与系统设计指标之间不存在直接的对应关系［2］。当数字反馈控制不能满足系统设计要求时，无法判断哪个控制系数需要调节以及如何调节，只能返回连续域（s域）阶段重新设计，甚至需要反复试探多次才能达到设计要求。

针对上述问题，基于状态空间理论和离散等效技术［3］，本文提出了Buck型变换器的数字电压控制及其设计流程，可一次性完成数字控制器的设计工作，避免了经典控制理论固有的反复试探性。

1 被控对象的跟踪控制模型

Buck型变换器的控制环路中，由功率级电路、数字脉冲宽度调制器（DPWM）和模／数转换器（ADC）构成了被控对象，如图1所示［4］。其中vG、vO、vref、iL、uU、eE和dD分别是Buck型变换器的输入电压、输出电压、参考电压、功率级电感电流、数字占空比、数字误差电压和模拟占空比。

图1 Buck型变换器的被控对象结构

选择电感电流和输出电压作为状态变量，得到功率级电路、DPWM和ADC的交流量状态方程分别为［5－6］：

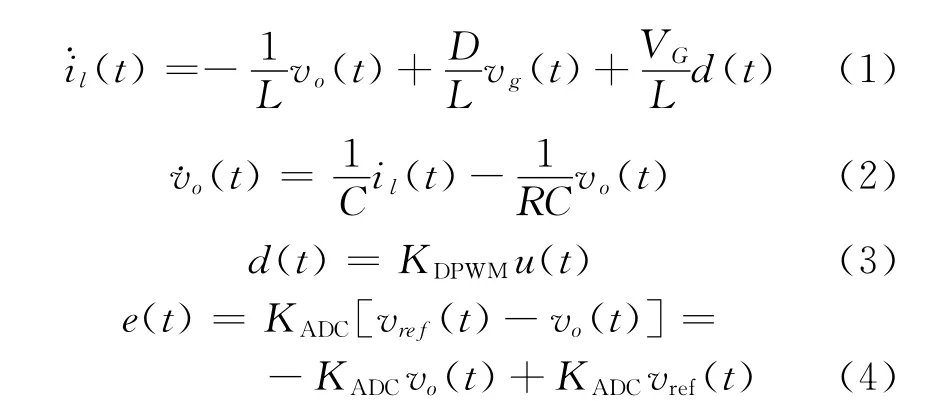
式中：L、C和R分别为功率级的滤波电感、滤波电容和负载电阻；VG和D分别为输入电压和模拟占空比的稳态直流量；il（t）、vo（t）、vg（t）和d（t）为对应的交流量；KDPWM和KADC分别为DPWM和ADC的传递函数；u（t）、e（t）和vref（t）分别为数字占空比、数字误差电压和参考电压的交流量。

式（1）和式（2）说明Buck型功率级电路的核心是LC滤波电路，式（3）和式（4）说明DPWM 和ADC可等效成常数传递函数的比例环节，所以图1所示的被控对象属于二阶谐振系统。为实现Buck型变换器的跟踪控制，需要在模／数转换器后面串行加入一个积分环节（复频域模型1／s），使得原被控对象由二阶系统升至三阶系统。设q是积分输出交流量，则存在下面关系式：

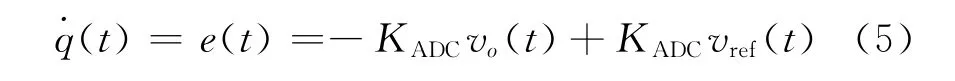
选择积分输出交流量作为第3个状态变量，合并式（1）、式（2）、式（3）和式（5），得状态方程模型：

式中：A为状态矩阵；B为输入矩阵。

输出方程为：

式中：C为输出矩阵；D为直接转移矩阵。

模型式（9）中包含了积分环节，便于实现Buck型变换器的跟踪控制，所以称该模型为被控对象的跟踪控制模型。

2 跟踪控制模型的可控性和可观性

系统可控矩阵是行满秩矩阵，则系统完全可控；系统可观矩阵是列满秩矩阵，则系统完全可观［1］，针对上述跟踪控制模型，分别得出对应的可控矩阵和可观矩阵为：

可控矩阵MC和可观矩阵MO的秩均等于3，分别是行满秩矩阵和列满秩矩阵，说明Buck型变换器的被控对象完全可控且完全可观，利用输入信号控制被控对象有意义，利用输出信号进行反馈控制可行。

3 数字电压控制

3.1 数字控制器结构

以跟踪控制模型的输出电压vO和积分输出量qQ作为反馈源，由比例环节F1和积分环节构成积分反馈支路，由F2构成电压反馈支路，形成Buck型变换器的电压反馈控制，如图2（a）所示。用Ts表示Buck型变换器的开关周期，采用数字滤波技术将积分环节转换成差分形式并作如下定义［3］：

得到如图2（b）中虚框所示的数字控制电路，它由2个乘法器和3个两输入加法器构成。

图2 电压反馈控制的Buck型变换器

3.2 控制系数计算公式

根据图2（a），Buck型变换器在数字电压控制下，闭环系统的状态空间模型和特征方程分别为：

式中：Asys为状态矩阵；Bsys为输入矩阵。

控制理论对一阶系统和二阶欠阻尼系统进行了深入研究，并根据极点之间的相对位置，将三阶系统近似等效成二阶欠阻尼系统或一阶系统进行分析。不妨给出便于系统设计的三阶特征方程：

式中：ζ、ωn和ζωn分别为阻尼系数、无阻尼振荡频率和衰减系数；p为复平面中的实极点距原点的距离。

当Buck型变换器被设计成近似二阶欠阻尼系统时，根据式（18）和式（19），得出控制系数计算公式为：

当Buck型变换器被设计成近似一阶系统时，控制系数计算公式为：

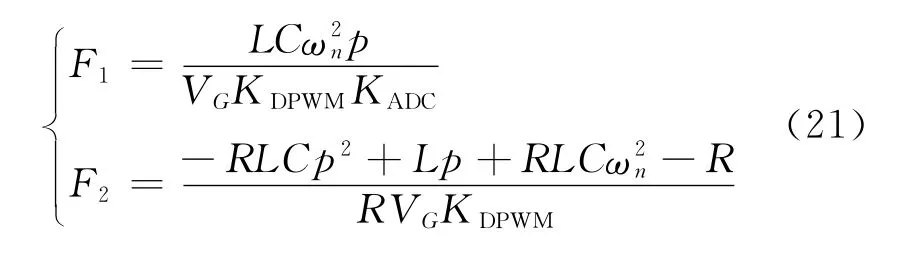
3.3 瞬态性能分析

控制系数F1对Buck型变换器瞬态性能的影响在参考文献［7］中进行了系统论述，本文仅对控制系数F2进行分析。根据图2（a），当F2＜0时（b＞0），电压反馈支路形成正反馈，导致Buck型变换器振荡；当F2＝0时（b＝0），电压反馈支路的作用消失，系统仅由积分反馈支路控制；当F2＞0时（b＜0），电压反馈支路属于负反馈，削弱了积分反馈支路对系统瞬态性能的影响，F2越大（｜b｜越大），削弱作用越强。因此，控制系数F2对瞬态性能的影响与控制系数F1的作用相反，如表1所示（F1＞0，F2＞0；↗：增大，↘：减小）。

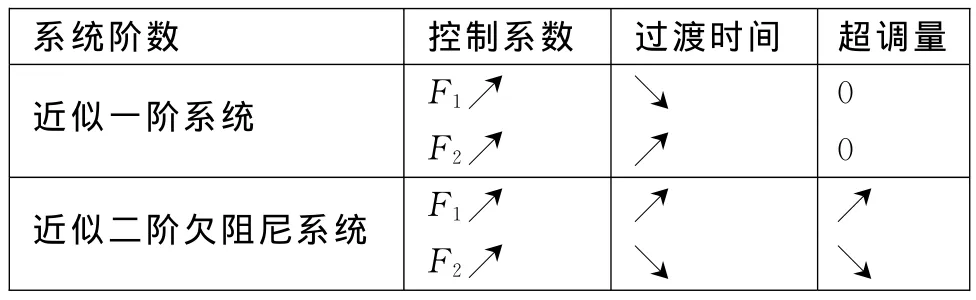
表1 控制系数的影响

4 数字电压控制设计流程

基于上述分析，得到Buck型变换器数字电压控制的设计流程如下：

（1）确定Buck型变换器的系统阶数。根据应用环境及瞬态响应的要求，确定Buck型变换器为近似二阶欠阻尼系统或近似一阶系统。

（2）计算控制系数F1和F2。根据选定的系统阶数，利用式（20）或式（21）计算控制系数。

（3）设计验证。利用仿真或测试等方法验证由F1和F2所确定的数字控制器是否满足Buck型变换器的设计指标。若满足，设计结束；若不满足，继续（4）。

（4）微调控制系数F1和F2。判断当前Buck型变换器的瞬态性能与设计指标的差距，并根据表1总结的规律，对控制系数进行微调，微调后返回（3）。

上述流程如图3所示。

5 仿真与测试

控制系数F1的验证见参考文献［7］，本文只验证控制系数F2对Buck型变换器瞬态性能的影响。利用Matlab／Simulink建立Buck型变换器模型，其系统参数为：fs＝200kHz，Ts＝5μs，L＝22.0μH，C＝22.0μF，R＝1.8Ω，VG＝5.0V，VO＝1.8V，KDPWM＝1／211，KADC＝210／5。

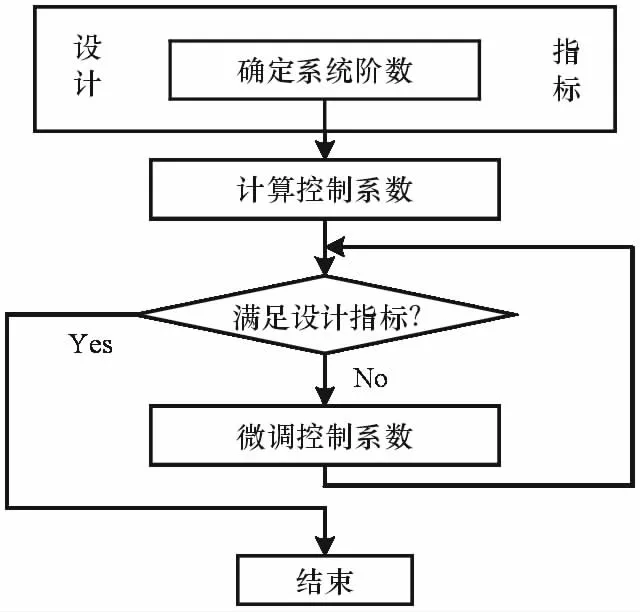
图3 数字电压控制的设计流程

针对负载电流发生0.2A的上跳变，固定a（F1·Ts）＝0.225，从0～2.7之间等步长地变化｜b｜（F2／KADC），并分别进行瞬态仿真，其结果统计在图4中。当｜b｜＝0时，电压反馈支路无效，积分反馈支路配置变换器为近似二阶欠阻尼系统；随着｜b｜增大（F2增大），电压反馈支路对积分反馈支路的削弱作用开始增强，促使变换器由近似二阶欠阻尼系统向近似一阶系统转换，过渡时间和超调量均逐渐减小；当｜b｜增大至2.1时，超调量减小至零，标志着Buck型变换器过渡至近似一阶系统；之后，过渡时间又随着｜b｜的增大而增加。在当前仿真环境下，过渡时间的最小值为130μs。上述仿真结果与表1所示的理论分析结果一致。

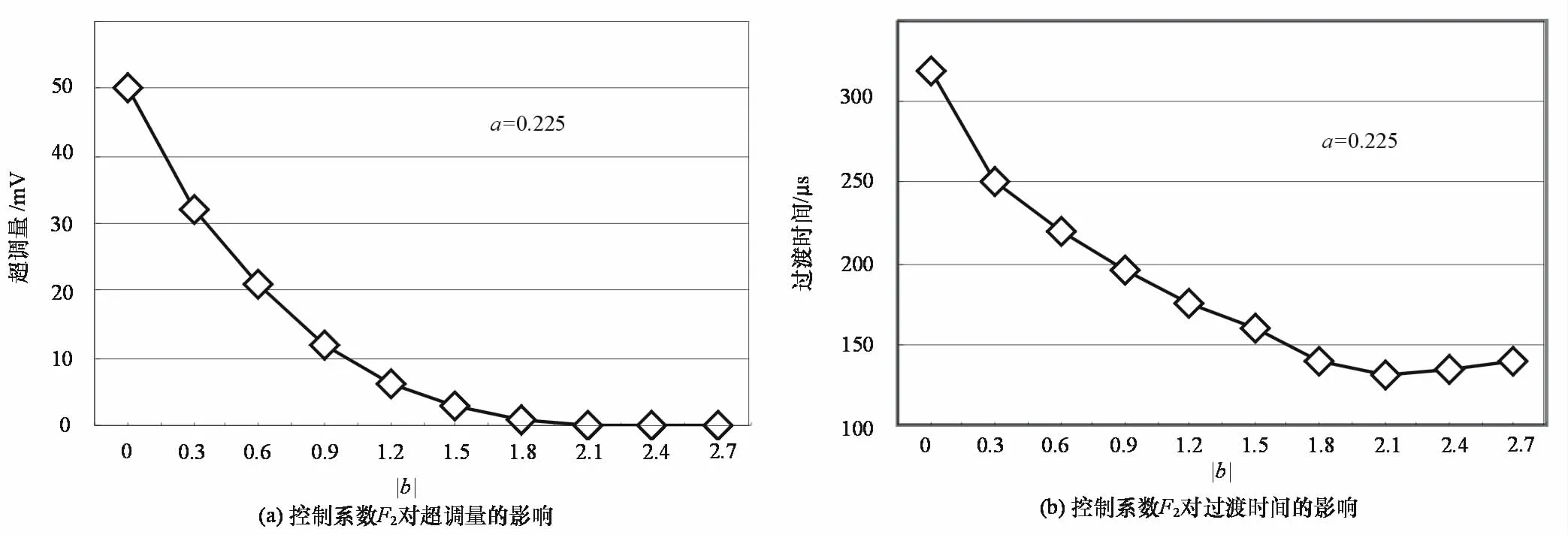
图4 控制系数F2对超调量和过渡时间的影响

为了进一步验证本文结论，保证系统参数与仿真模型一致的前提下，设计了基于FPGA的数字Buck型变换器，并在其上实施所提的数字电压控制，测试曲线如图5所示。测试结果表明：数字电压控制实现了Buck型变换器的稳态跟踪控制；随着控制系数｜b｜的增大，变换器由近似二阶系统向近似一阶系统过渡，验证了数字电压控制的理论分析和仿真结果的正确性。

图5 电压反馈控制的输出电压测试曲线

6 结束语

基于状态空间理论，提出了Buck型变换器的数字电压控制，针对系统超调量和过渡时间2个指标，分析了控制参数对变换器瞬态性能的影响，给出了数字电压控制的设计流程，用以指导数字控制器的一次性设计工作，有效地避免了经典控制理论固有的反复试探性。仿真与测试结果验证了所提数字电压控制的有效性及理论分析的正确性。

［1］胡寿松.自动控制原理（第5版）［M］.北京：科学出版社，2007.

［2］俞 立.现 代 控 制 理 论 ［M］.北 京：清 华 大 学 出 版社，2007.

［3］Gene F F，DAVID J P，MIichael W.Digital Control of Dynamic Systems ［M］.Reading，MA：Addison－Wesley，1998.

［4］张卫平.开关变换器得建模与控制［M］.北京：中国电力出版社，2006.

［5］Erichson Robert W，Maksimovic Dragan.Fundamentals of Power Electronics［M］.New York：Kluwer Academic Publishers，2000.

［6］Benjamin J P，Aleksandar P，Art Z，et al.High－frequency digital PWM controller IC for DC－DC converters［J］.IEEE Transactions on Power Electronics，2003，18（1）：438－446.

［7］李峰，魏廷存，郑宇亮.单参数控制的数字DC－DC变换器设计及其FPGA实现［J］.计算机测量与控制，2012，20（4）：1042－1045.