一种稳健接收波束形成算法
郑均杰
(解放军92785部队,秦皇岛066000)
0 引 言
波束形成是阵列信号处理的重要组成部分,在雷达、声纳、无线通信等领域有着广泛的应用。其主要目的是有效地提取信号,同时可以最大限度地抑制干扰和噪声。对于经典理论而言,Capon波束形成在一定条件下有较好的性能,但在实际工程中,由于阵列天线并非理想化,阵元之间的误差、互耦等影响都会导致模型失配,致使Capon波束形成的性能下降。为此,稳健波束形成技术已逐渐成为理论和工程界关心的重要课题[1-4]。
1 Capon波束形成
对于一个具有M个阵元的阵列,R是阵列采样协方差矩阵,设R>0,且有:

式中:ak,k=0,1,…K为第k个信号的方向向量;为第k个信号的功率;(·)*为共轭转置运算;Q为噪声项。
假设式(1)中第1项为信号。对于经典Capon波束形成算法就是期望信号的方差最小且无畸变。其可以描述为:

应用Lagrange乘数法,很容易得到以上问题的解:


另外,Capon波束形成也可以表示为协方差拟合的形式,即:
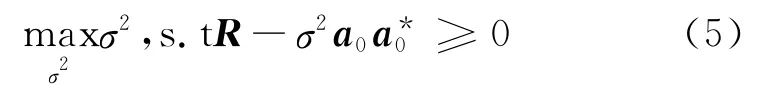
可以验证2种Capon波束形成的等价性。
协方差拟合Capon波束形成算法可以描述为:给定R和信号方向a0,将最大的σ2作为信号功率的估计,且满足协方差矩阵的残差非负定,即R-
2 稳健接收波束形成
稳健接收波束形成方法主要由A.B Gershman,R.Lorenz等提出,其优化目标是最不利情况下的信干噪比。下面介绍在DOA失配情况下稳健接收波束形成方法[2]。
设信号的真实方向为a0,期望方向为0,失配向量δ为:

通常认为失配向量δ是有界的,即:

式中:ε为一常数,它表示了DOA估计可能出现的最大失配。
把经典Capon波束形成做一些推广:

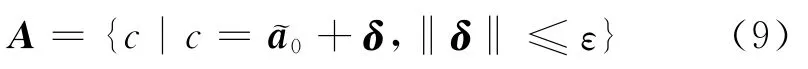
把不失真约束拓展到真实信号方向所在的集合A上等价于对A中最不利情况下的方向进行无失真约束[4-6]。
对式(8)进行等价变形:

可以证明以上问题(10)可以转化为:

将式(10)做一等价转化:

式(12)可以看成一个二次锥规划的问题。首先,把目标函数转化成线性函数,对R做Cholesky分解[6-7]:

利用上式,有:
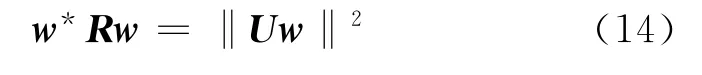
优化问题(12)可以改写为:

为了方便运算,需要把以上问题转化成实数形式,令:
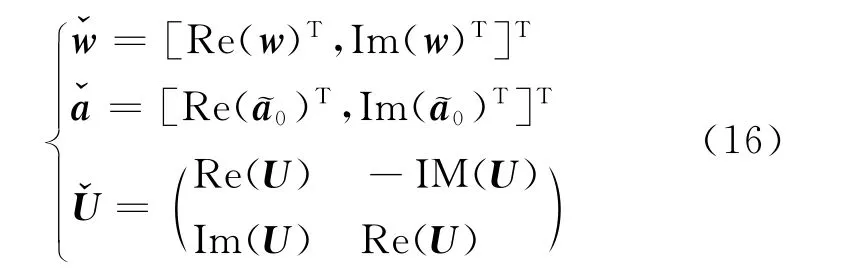
式(15)可以表示为实值向量和矩阵形式:

显然,上式是一个二次锥规划,可以直接用凸优化工具求解,则最优权值可以由下式计算得到:

为了更加深入地分析问题的本质,现在考虑等价的等式约束问题:

借助Lagrange方法,构造Lagrange函数:

式中:v为Lagrange乘子。

可以得到:

由:

式中:Rs为信号协方差矩阵;Ri+n为干扰加噪声协方差矩阵。
由于信号干扰加噪声比(SINR)是权向量的任意尺度变换的不变量,因此,上式可以转化为:

从而有:

从式(24)可以看到,对于稳健Capon波束形成问题可以归结为对角加载问题。但与传统的固定系数对角加载不同,稳健Capon波束形成问题的加载系数是ε/‖w‖,其直接与ε相关,可以认为,这样的对角加载是与信号的DOA失配相匹配的。因此,稳健Capon波束形成就成了如何求得加载系数,即归结到如何求得‖w‖,则:

对式(25)两边取范数平方,可以得到:

令τ=‖w‖>0,式(26)可以转化为:
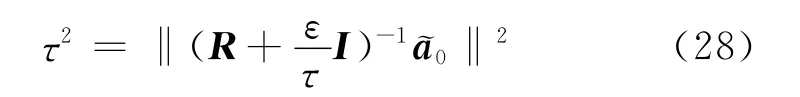
为了简化上式,对R做特征分解R=UΓU*,代入到以上等式中,可得:
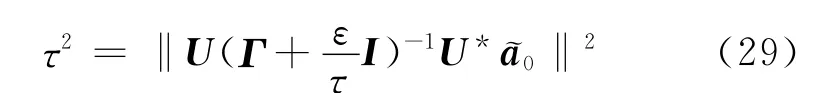

考虑到τ>0,这样τ的求解问题就转化为:


方程f(τ)=0的根就在上,其中:

应用牛顿迭代算法,可以直接求得‖w‖,根据式(25)可以求得信号DOA失配与干扰加噪声的权值。
3 仿真
以均匀线阵进行仿真。信号和噪声设为零均值复高斯过程,对于第k个信号,其信噪比为:
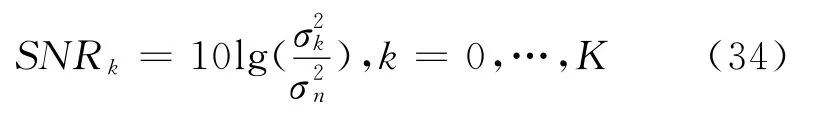
最优信噪比由下式给出:

仿真中对比的算法如下:经典Capon波束形成算法,缩写为 “Standard CB”;稳健接收波束形成算法[8-9],缩写为 “Ellip-Uncertainty RCB”。
采用10阵元线性阵列,阵元间距为半波长。期望信号(SOI)位于0°,信噪比10dB;2个干扰位于25°和50°,信噪比为20dB,噪声方差为1。
(1)无角度失配
信号DOA精确已知情况下各波束形成器的接收方向图(N=1 000)如图1所示,各波束形成器输出的SINR与数据长度之间的关系(100次独立仿真的结果)如图2所示,各波束形成器输出的SINR与期望信号信噪比(SNR)之间的关系(100次独立仿真的结果,N=200)如图3所示。

图1 信号DOA精确已知情况下各波束形成器的接收方向图

图2 信号DOA精确已知情况下各波束形成器输出的SINR与数据长度之间的关系

图3 信号DOA精确已知情况下各波束形成器输出的SINR与期望信号SNR之间的关系
(2)存在1°角度失配
信号DOA失配1°情况下各波束形成器的接收方向图(N=1 000)如图4所示,各波束形成器输出的SINR与数据长度之间的关系(100次独立仿真)如图5所示,各波束形成器输出的SINR与期望信号SNR之间的关系(100次独立仿真,N=200)如图6所示。

图4 信号DOA失配1°情况下各波束形成器的接收方向图

图6 信号DOA失配1°情况下各波束形成器输出的SINR与期望信号SNR之间的关系
从仿真结果可以看出,当信号DOA精确已知时,经典Capon算法和圆约束下的稳健波束形成算法均具有良好的波束,即在0°方向上形成主峰,在25°和50°方向上形成凹陷;当信号DOA出现1°角失配时,经典Capon算法在0°方向形成凹陷,这可能会造成信号的漏检,而圆约束下的稳健波束形成算法在失配情况下,依旧在0°信号方向形成主峰。另外,圆约束下的稳健波束形成算法的各波束形成器输出信噪比接近于理想情况,且随观测数据和输入信噪比变化明显优于经典Capon算法。
4 结束语
仿真验证了空域滤波稳健Capon波束形成算法的性能。在实际环境中,精确测得期望信号DOA通常是不可能的,当信号DOA出现失配、局部相干和非相干散射等情况时,稳健接收波束形成算法的显著优于经典的Capon波束形成算法。仿真说明,稳健波束形成方法在阵列流型失配和少观察数据量下具有稳健的性能。
[1]Gershman A B,Sidropoulos N D,Shahbazpanahi S,Bengtsson M,Ottersten B.Convex optimization-based beamforming[J].IEEE Signal Processing Magazine,2010,27(3):62-75.
[2]Vorobyov S,Gershman A B,Luo Z Q.Robust adaptive beamforming using worst-case performance optimization:A solution to the signal mismatch problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.
[3]Vorobyov S,Gershman A B,Luo Z Q,Ma N.Adaptive beamforming with joint robustness against mismathched signal steering vector and interference nonstationary[J].IEEE Signal Processing Letter,2004,11(1):108-111.
[4]Shahbazpanahi S,Gershman A B,Luo Z Q.Robust adaptive beamforming for general-rank signal models[J].IEEE Transactions on Signal Processing,2003,51(5):2257-2269.
[5]Vorobyov S,Chen H,Gershman A B.On the relationship between robust minimum variance beamformings with probablilistic and worse-case distortionless response constraints[J].IEEE Transactions on Signal Processing,2008,56(3):5719-5724.
[6]Lorenz R,Boyd S P.Robust minimum variance beamforming[J].IEEE Transactions on Signal Processing,2005,53(2):1684-1696.
[7]Stoica P,Wang Zhisong,Li Jian.Robust Capon beamforming[J].IEEE Transactions on Signal Processing Letters,2003,10(6):172-175.
[8]Li J,Stoica P,Wang Z.On robust Capon beamforming and diagonal loading[J].IEEE Transactions on Signal Processing,2003,51(3):1702-1715.
[9]Capon J.High resolution frequency-wavenumber spectrum analysis[J].IEEE Signal Processing Magazine,1969,57(5):1408-1418.

