基于皮尔逊Ⅲ型分布的汉口站年最小月流量趋势性分析

江 聪，熊立华

（武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

基于皮尔逊Ⅲ型分布的汉口站年最小月流量趋势性分析

江 聪，熊立华

（武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

在变化环境下，对水文时间序列的非一致性研究变得非常重要。经典线性回归模型在传统的水文序列趋势性分析中有广泛的应用，该模型假定水文变量服从正态分布，这与我国现行的水文频率分析计算中推荐选用的皮尔逊Ⅲ型频率分布（简称PⅢ分布）并不相符。提出采用基于PⅢ分布的回归模型对汉口水文站59 a间的年最小月流量序列进行趋势性分析。研究发现基于PⅢ分布的回归模型比基于正态分布的回归模型能更好地揭示水文序列频率分布的时变特征。在此基础上采用灵活性较强的多项式对水文序列的趋势性进行了分析。

趋势性分析；回归模型；正态分布；PⅢ分布；年最小月流量

1 研究背景

现行的水文频率分析方法的一个基本前提条件是水文序列必须满足一致性［1］。近几十年来全球气候的变化和人类活动的影响，使水文序列失去一致性，对工程水文设计和水电工程的正常运行造成了极不利的影响，因此对非一致性水文序列进行研究具有重要意义。目前国内非一致性水文频率分析计算的内容主要有变点分析、趋势性分析等［2－3］。线性回归模型是分析检验水文序列趋势性和非一致性水文还原计算的重要工具，并在实际中得到广泛应用。熊立华等［4］应用一元线性回归模型分析了长江宜昌站1882—2001年间的年最大、年最小和年平均流量序列，发现三者均具有随时间减小的趋势，并对回归方程的显著性进行了检验。谢平等［5］建立了潮白河年径流量随时间的线性回归方程，并对线性回归系数进行了显著性检验，采用分布合成的方法进行了非一致性水文序列的合成计算，分析了北京市的水安全问题。赵锐锋［6］等也运用线性回归的方法分析了塔里木河干流4个水文站年径流量的变化趋势。

以上回归模型均假设水文序列服从正态分布，广义线性模型认为这个模型可以被推广其他情况，即因变量（随机变量）是非正态分布的。Gabriele等人［8－9］应用基于耿贝尔、伽马、对数正态分布的GAMLSS模型（Generalized Additive Models for Location，Scale and Shape）分别对罗马地区长期的降水和气温序列以及美国Little Sugar Creek流域的年最大洪峰序列进行了趋势和成因分析，并且取得较好的拟合效果。在我国一般认为水文序列服从PⅢ型频率分布［10］，运用基于正态分布假设的回归模型对不满足正态分布的水文序列进行趋势性分析显然是不合理的，在还原计算中势必会造成较大误差。本文将引入基于PⅢ分布的回归模型对汉口水文站59 a间的年最小月流量序列进行趋势性分析，在此基础上建立二次多项式回归模型，以更加灵活地反应序列的趋势变化。

2 基于正态分布的水文序列趋势性分析

假设水文序列Y与时间t之间存在相关关系［11］：

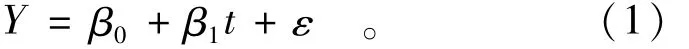
称方程Y＝β0+β1t为经验型回归方程，简称回归方程，其中：β0，β1为回归系数；ε为近似值与真值Y的偏差，称为残差，通常认为ε是服从正态分布的随机变量。现将一组水文序列观测值yi和相应的时间值ti（ i＝1，2，…，n）代入式（1）得由序列的均值E（yi）与方差D（yi）可以由如下公式（3），公式（4）表示：

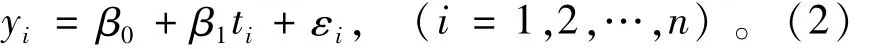
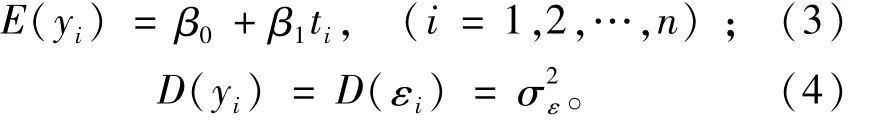
因此水文序列观测值yi服从正态分布N（β0+β1ti，。最后运用最小二乘法或极大似然法对模型的参数进行求解后即可得到序列的回归方程。

3 基于PⅢ分布的水文序列趋势性分析

3.1 基于PⅢ分布回归模型的定义

首先将PⅢ分布概率密度函数写为

其中μ，σ，ν分别为PⅢ分布位置、尺度和形状参数，它们和PⅢ分布的均值E（Y）、变差系数CV、偏态系数CS关系如下：

与基于正态分布的回归模型类似，基于PⅢ分布的回归模型也被认为水文序列与时间之间存在相关关系

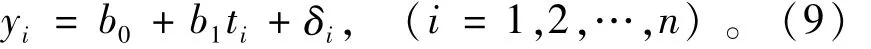
式中：yi为水文序列的实际观测值，yi～PⅢ（b0+ b1ti，σ，ν）分布，δi为模型残差。

3.2 模型参数求解

本文将采用最大似然法［11］求解公式（9）的未知参数为b0，b1，σ，v，令向量θ＝（b0，b1，σ，v）T。

设Y1，Y2，…，Yn为来自Y中的样本，分布概率密度函数为），且θ∈Θ（Θ为θ的可能取值范围），又设y1，y2，…，yn为相应样本Y1，Y2，…，Yn中的一个样本值，令

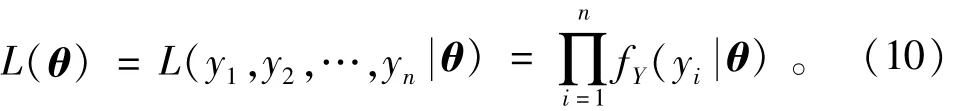
这里L（θ）为样本的似然函数。为简化，似然函数一般取似然函数的对数，即对数似然函数ln L（θ），若

根据上述公式，下面给出PⅢ分布的对数似然函数

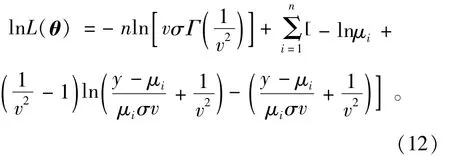
式中：μi＝b0+b1ti（i＝1，2，…，n）；σ＝CV；v＝CS／2，然后运用牛顿－拉普森法对参数进行求解［12］。

3.3 模型拟合效果评价

为对比不同回归模型的拟合效果，引入全局拟合偏差GD和AIC准则作为评定标准［12］，定义分别如下：

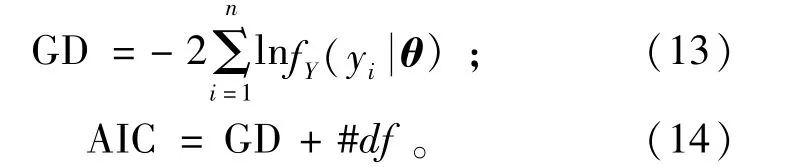
式中：＃为模型每个有效自由度的惩罚系数，一般取2；df为模型的有效自由度。GD反映了模型的整体拟合效果，GD越小说明模型的拟合偏差越小。但为防止过度拟合，在GD的基础上加上惩罚项＃df得到AIC准则判断值，在模型自由度不同的情况下，通过对比AIC值进行模型优选。

判断模型的拟合效果，残差的概率分布检验也是重要的一方面内容。为了便于对比不同分布类型模型残差的分布状况，首先根据相应的分布类型对残差进行标准正态化处理［13］：

式中：ri为标准正态化的残差；Φ－1为正态分布概率函数的反函数其中F（）为相应分布的概率函数，例如假设水文序列服从PⅢ分布，F（）即为PⅢ分布的概率函数。标准正态化的残差序列越接近于标准正态分布，说明模型产生的残差序列越合理。然后推求模型理论残差

最后以理论残差Mi横坐标，以实际残差ri纵坐标，可得正态QQ图。图中点与1∶1的直线偏差越小，说明残差的实际值与理论值越接近，模型的拟合效果越好。

4 基于PⅢ分布的汉口站年最小月流量趋势性分析

汉口水文站位于长江与汉江交汇处的下游河段，上游控制面积约为149万km2，是长江干流设站最早的水文站之一。由于近几十年来，长江流域地区降水、蒸发条件和土地利用状况都发生了很大变化，同时大规模的水利工程建设，尤其是具有较大调蓄能力的水库的修建，这些方面因素都不同程度上改变了汉口站上游流域的产汇流条件及流域调蓄能力，使该站水文序列发生变异。秦年秀等［15］分析了1870—2000年间汉口站的多年平均流量序列，发现年平均流量有减少的趋势，同时分析了各月的平均流量序列，发现近些年来1—4月及7月份的平均流量有增加的趋势，其他月份有减少的趋势。选取汉口站1952—2010年间共59 a的年最小月流量序列，运用基于PⅢ分布的回归模型进行趋势性分析，同时对比基于正态分布回归模型的分析结果，比较两者的优劣。

4.1 序列初步分析

首先采用Mann-Kendall（简称M-K）法对序列进行趋势显著性检验，同时应用基于正态分布的回归模型对序列进行趋势性分析。计算结果见表1。

表1 M-K检验及基于正态分布趋势性分析的计算结果Table 1 Results of M-K test and trend analysis based on normal distribution

当显著水平取α＝5%时，Z（1－α／2）＝1.96，由于ZMK＞Z（1－α／2），从M-K检验的结果看，年最小月流量序列有比较明显的趋势；同样取显著水平α＝5%，线性趋势临界相关系数Rα＝0.256，而实际资料计算的相关系数R为0.480，显然，序列的线性趋势是存在的［11］，由于R＞0，因此年最小月流量序列具有显著的增加趋势，线性趋势线见图1。

图1 基于正态分布的趋势性分析Fig.1 Trend analysis based on normal distribution

4.2 一致性假设下的频率分析

假设汉口站59 a间的年最小月流量序列满足一致性，分别采用最大似然法估算服从正态分布和PⅢ分布时的统计参数，结果见表2。

表2 基于正态分布和PⅢ分布的统计参数最大似然估计Table 2 M aximum likelihood estimation of statistical parameters based on normal distribution and PⅢdistribution

根据计算所得统计参数，绘出正态分布和PⅢ分布的频率曲线（见图2）。基于正态分布的频率曲线大部分偏离实测点据，而基于PⅢ分布的频率曲线的拟合程度要明显好于前者，因此可以认为序列更加接近于服从PⅢ分布。

图2 基于正态分布和PⅢ分布频率曲线的拟合对比Fig.2 Com parison between the fitting results of the frequency curves based on normal distribution and PⅢdistribution

4.3 基于PⅢ分布的非一致性频率分析

下面采用基于PⅢ分布的回归模型对年最小月流量序列进行趋势性分析，根据最大似然法求解参数，计算结果见表3。

表3 基于PⅢ分布趋势性分析的计算结果Table 3 Results of trend analysis based on PⅢdistribution

比较表1和表3，发现基于PⅢ分布的回归模型计算得到的回归方程与基于正态分布模型计算得到的结果略有不同，截距b0有所增加，而直线的斜率b1有所减小，较原来的拟合直线平缓（见图3）。由于全局拟合偏差GD较基于正态分布回归模型的GD有所减小，这说明基于PⅢ分布的回归模型的拟合效果要优于基于正态分布的回归模型。尽管基于PⅢ分布的回归模型的自由度较基于正态分布的回归模型的自由度要多一个，但根据AIC判断准则，基于PⅢ分布的回归模型的值仍小于后者，因此从模型的整体效果看，基于PⅢ分布的回归模型还是要优于基于正态分布的回归模型。

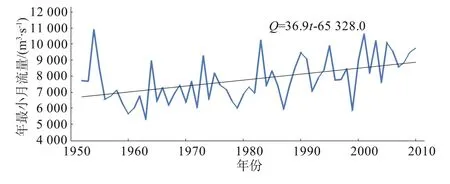
图3 基于PⅢ分布的趋势性分析Fig.3 Trend analysis based on PⅢdistribution

模型拟合产生的残差序列的分布状况可以反映原序列是否符合相应的分布。为便于比较，将2种模型产生的残差序列进行标准正态化处理，然后分别计算残差序列的均值、方差和偏态系数（见表4）。2种模型正态标准化的残差序列的均值和方差都非常接近，且基本接近于标准正态分布的统计参数（均值为0，方差为1）。但是在偏态系数方面，基于正态分布的回归模型产生的残差仍具有相当大的偏度，而基于PⅢ的回归模型产生的残差的偏度已经很小，基本接近于0，可以认定残差序列符合正态分布。

表4 基于正态分布和PⅢ分布回归模型的残差分析表Table 4 Residual analysis for the regression models based on normal distribution and PⅢdistribution

正态QQ图可以比较直观地反映正态标准化的残差序列分布状况，2种模型的正态QQ图见图4。基于正态分布回归模型的实际残差与理论残差之间出现了较明显的偏差，中部大部分点偏离了理论直线；基于PⅢ分布回归模型的残差除两端的少数点之外，大部分点与理论直线几乎重合，因此从残差分析方面来看，基于PⅢ分布的回归模型的拟合效果还是好于基于正态分布的回归模型。

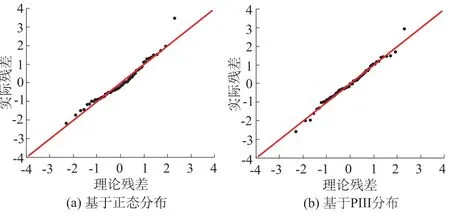
图4 回归模型的正态QQ图Fig.4 Normal QQ plots of regression models

综上所述，无论从模型的AIC判断准则还是残差分析，在汉口站年最小月流量序列的趋势性分析中，基于PⅢ分布的回归模型要明显优于基于正态分布的回归模型。

4.4 基于二次多项式回归的趋势性分析

对于较长的水文序列，其整体的趋势变化可能表现为增加或减少，但是各时间段趋势变化往往又不是单一的，如果用一元一次方程来描述整个序列的变化，势必会造成在某些时间段内会出现偏差。从5年滑动平均过程线（图2）来看，整个序列并不是完全一致地呈现递增趋势，在前期甚至出现了递减的趋势。为灵活地描述各个时段的趋势变化特征，下面引入二次多项式来反映整个序列的变化过程，具体计算与上类似，只是在均值中加入二次项t2，增加一个二次项系数b2，建立回归方程y＝b0+ b1t+b2t2+δ′。计算结果见表5。

表5 基于二次多项式回归的趋势性分析计算结果Table 5 Results of trend analysis based on quadric polynom ial regression

对比表3和表5中的计算结果可以看出，GD和AIC判断准则值都明显减少；拟合过程线基本上反映出了不同时段序列趋势变化的特征（见图5）；同时比较图6中实际点在不同概率（5%，25%，50%，75%和95%）分位曲线之间的分布状况，二次多项式回归模型的分布状况较一次回归模型也更为合理，这说明在描述序列趋势变化方面二次多项式回归模型的效果要优于一次回归模型。

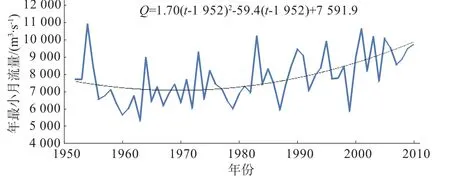
图5 基于二次回归模型的趋势性分析Fig.5 Trend analysis based on quadric polynom ial regression

5 结 语

在变化环境下，对水文时间序列的非一致性研究变得非常重要。经典线性回归模型在传统的水文序列趋势性分析中有广泛的应用，该模型假定水文变量服从正态分布，这与我国现行的水文频率分析计算中推荐选用的PⅢ型频率分布并不相符。本文中重点介绍了基于PⅢ分布的回归模型，并且用该模型对汉口水文站59 a间的年最小月流量序列进行了趋势性分析。无论从模型的AIC判断准则还是残差分析，基于PⅢ分布的回归模型在汉口站年最小月流量序列的趋势性分析中要明显优于基于正态分布的回归模型。因此，基于PⅢ分布的回归模型比基于正态分布的回归模型能够更好地反映序列的分布特征。研究还发现，引入二次多项式来描述较长序列的趋势变化，能够更加灵活地描述水文序列趋势的变化特征。

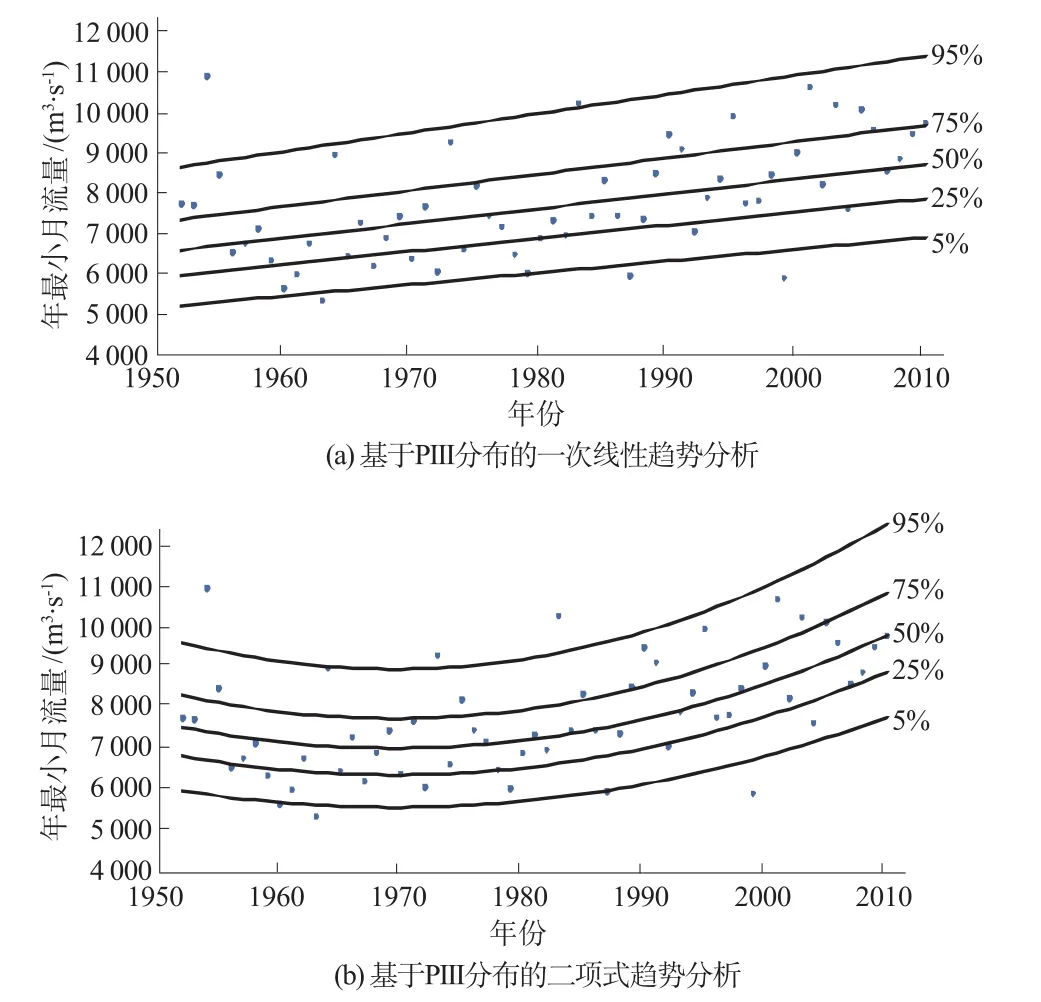
图6 概率分位曲线Fig.6 Centiles curves

在水文序列的趋势性分析中，本文作者只考虑均值随时间的变化，但水文序列的趋势性变化也可能是表现在方差和偏态系数方面，在今后的非一致性水文序列分析中考虑多种统计参数的时变将是研究的重要内容之一。

［1］ 梁忠民，胡义明，王 军.非一致性水文频率分析的研究进展［J］.水科学进展，2011，22（6）：864－871.（LIANG Zhong-min，HU Yi-ming，WANG Jun.Advances in Hydrological Frequency Analysis of Non-stationary Time Series［J］.Advances in Water Science，2011，22（6）：864－871.（in Chinese））

［2］ 王文圣，丁 晶，金菊良，等.随机水文学（第二版）［M］.北京：中国水利水电出版社，1997.（WANG Wen-sheng，DING Jing，JIN Ju-liang，et al.Stochastic Hydrology（Second Edition）［M］.Beijing：China Water Power Press，1997.（in Chinese））

［3］ 谢 平，陈广才，雷红富，等.水文变异诊断系统［J］.水力发电学报，2010，29（1）：85－91.（XIE Ping，CHEN Guang-cai，LEIHong-fu，et al.Hydrological Alteration Diagnosis System［J］.Journal of Hydroelectric Engineering，2010，29（1）：85－91.（in Chinese））

［4］ XIONG Li-hua，GUO Sheng-lian.Trend Test and ChangepointDetection for the Annual Discharge Series of the Yangtze River at the Yichang Hydrological Station［J］.Hydrological Sciences Journal，2004，49（1）：99－112.

［5］ 谢 平，陈广才，韩淑敏，等.从潮白河年径流频率分布变化看北京市水资源安全问题［J］.长江流域资源与环境，2006，15（6）：713－717.（XIE Ping，CHEN Guang-cai，HAN Shu-min，etal.Problems in the Security of Water Resources in the City of Beijing Reflected from the Change in Annual Runoff Frequency Distribution in Chaobaihe Basin［J］.Resources and Environment in the Yangtze Basin，2006，15（6）：713－717.（in Chinese））

［6］ 赵锐锋，陈亚宁，李卫红，等.1957年至2005年塔里木河干流径流变化趋势分析［J］.资源科学，2010，32（6）：1196－1203.（ZHAO Rui-feng，CHEN Ya-ning，LI Wei-hong，et al.Trends in Runoff Variations of the Mainstream of the Tarim River during the Last50 Years［J］.Resources Science，2010，32（6）：1196－1203.（in Chinese））

［7］ 乔治·H·邓特曼.广义线性模型［M］.上海：格致出版社，2011.（DUNTERMAN G H.Generalized Linear Model［M］.Shanghai：Gezhi Press，2011.（in Chinese））

［8］ GABRIELE V，JAMES A S，FRANCESCO S，et al.Flood Frequency Analysis for Nonstationary Annual Peak Records in an Urban Drainage Basin［J］.Advances in Water Resources，2009，32（8）：1255－1266.

［9］ GABRIELE V，JAMES A S，FRANCESCO S.Nonstationary Modeling of a Long Record of Rainfall and Temperature over Rome［J］.Advances in Water Resources，2010，33（10）：1256－1267.

［10］詹道江，叶守泽.工程水文学［M］.北京：中国水利水电出版社，2000.（ZHAN Dao-jiang，YE Shou-ze.Engineering Hydrology［M］.Beijing：China Conservancy and Hydropower Press，2000.（in Chinese））

［11］黄振平.水文统计学［M］.南京：河海大学出版社，2003.（HUANG Zhen-ping.Hydrologic Statistics［M］.Nanjing：Hohai University Press，2003.（in Chinese））

［12］RIGBY R A，STASINOPOULOSDM.Generalized Additive Models for Location Scale and Shape［J］.Applied Statistics，2005，54（3）：507－554.

［13］RIGBY B，STASINOPOULOSM.A Flexible Regression Approach Using GAMLSS in R［M］.Lancaster：Univer-sity of Lancaster，2009.

［14］薛 毅，陈立萍.统计建模与R软件［M］.北京：清华大学出版社，2006.（XUE Yi，CHEN Li-ping.Statistical Modeling and R Software［M］.Beijing：Tsinghua U-niversity Press，2006.（in Chinese））

［15］秦年秀，姜 彤，许崇育.长江流域径流趋势变化及突变分析［J］.长江流域资源与环境，2005，14（5）：589－594.（QIN Nian-xiu，JIANG Tong，XU Chong-yu.Trend and Abruption Analysis on the Discharge in the Yangtze Basin［J］.Resources and Environment in the Yangtze Basin，2005，14（5）：589－594.（in Chinese））

（编辑：赵卫兵）

长江科学院派员赴贵州福建进行石漠化、红壤流失治理现状与技术应用考察

2013年5月28日至6月1日，长江科学院水土保持所、农业水利所所长张平仓率孙蓓、孙佳佳参加了由水利部科技推广中心组织的贵州石漠化和福建红壤流失治理现状与技术应用考察。考察团由水利部科技推广中心肖新民处长率领，参加人员包括水利部科技推广中心张冠华博士、许文盛博士，中国科学院南京土壤所梁音教授，厦门理工学院傅海燕副教授及江苏艾特克环境工程设计研究院、深圳市微润灌溉技术有限公司、北京亚盟达生态技术有限公司、深圳市天源新能源有限公司、北京德科创源科技有限责任公司、北京水创新能科技有限公司等高新科技企业代表。贵州省水利厅、长汀县人民政府的领导和技术人员热情接待了考察团一行。

考察团查勘了贵州长顺典型喀斯特地貌、石漠化以及治理现状，并与水利厅水保处、贵州省水科院的领导及专家进行了交流座谈；查勘了福建长汀红壤流失及崩岗发育的现状和治理，并与长汀县领导及相关技术人员进行了交流座谈。

在座谈中，各高新科技企业专家针对当地地貌和区域特征，特别是季节性干旱和严重水土流失情况交流了W-OH高新复合材料应用技术、微润灌溉技术、工程护岸生态治理技术、新能源提水技术等高新技术，地方领导及技术人员对各项技术给予了充分肯定与高度评价，并与考察团专家共同商讨了将各项技术应用于当地水土保持工作的应用前景和治理模式。

（摘自：长江水利科技网）

Trend Analysis on the Annual M inimum M onthly Runoff Series of Yangtze River at Hankou Hydrological Station Based on Pearson Type IIIProbability Distribution

JIANG Cong，XIONG Li-hua
（State Key Laboratory ofWater Resources and Hydropower Engineering Sciences，Wuhan University，Wuhan 430072，China）

It is very important to research the inconsistency（or nonstationarity）of hydrological time series under changing circumstance.Classical regression models，which are widely used in traditional hydrological trend analysis，are based on the assumption that the hydrological variables follow the normal distribution.However，this assumption does not consist with the practical findings in China thatmost hydrological random variables follow the Pearson type III（PⅢ）distribution.In this paper，the regression model based on the assumption of the PⅢdistribution is introduced to analyze the trend of annualminimum monthly runoff series of the Yangtze River at Hankou hydrological station observed over the period of 1952-2010.It is found that the regression model based on the PⅢdistribution ismore effective than the regressionmodel based on the normal distribution in fitting the trend of hydrological series.Furthermore，themore flexible polynomial is used to analyze the trend of the hydrological series.

trend analysis；regressionmodel；normal distribution；PⅢdistribution；annualminimum monthly runoff

TV121.2

A

1001－5485（2013）07－0016－06

10.3969／j.issn.1001－5485.2013.07.004

2012－06－29；

2012－08－06

国家自然科学基金重大项目（51190094）；国家自然科学基金项目（51079098）

江 聪（1989－），男，河北宁晋人，硕士研究生，主要从事水文水资源方面的研究，（电话）13659831242（电子信箱）jc1207＠whu.edu.cn。