K0≠1时基础软弱下卧层临界埋深的讨论

黄朝煊，袁文喜，方咏来

（浙江省水利水电勘测设计院，杭州310002）

K0≠1时基础软弱下卧层临界埋深的讨论

黄朝煊，袁文喜，方咏来

（浙江省水利水电勘测设计院，杭州310002）

通过数学理论推导，给出了考虑静止土压力系数K0≠1时的条形基础的地基临界荷载P1／4，并与国标《建筑地基基础设计规范》（GB50007—2011）中相应公式（5.2.5条）进行了对比分析，认为国标公式过高估计了地基承载力，而本文公式相对较合理。当基础受力层范围内存在软弱下卧层时，国标中“5.2.7”条给出了软弱下卧层承载力验算公式，但未说明软弱下卧层埋深超过多少时可不考虑软弱下卧层影响，采用已推导的地基承载力公式，通过无量纲化推导计算，给出了软弱下卧层相对临界埋深（Hcr／b）与基础相对埋深（d／b）之间的关系式。最后通过实例计算，得出了不同基础宽度、不同软弱下卧层抗剪强度指标下的相对临界埋深（Hcr／b）关系曲线，认为软弱层抗剪强度指标越大、上层土内摩擦角越大，则软弱下卧层相对临界埋深Hcr就越小，其不利影响就越小。

地基承载力；静止土压力系数；软弱下卧层；软弱层临界深度

对于地基下存在软弱下卧层时的地基承载力验算，国标《建筑地基基础设计规范》（GB50007—2011）［1］中给出了相应的软弱层承载力验算公式。实际中，当软弱下卧层埋深较大时，浅基础设计中是完全可不考虑软弱下卧层影响的，只有当软弱下卧层埋深较小时，浅基础设计中才需采用国标中相应验算公式进行复核，基于此，本文将对此问题进行深入研究。

1 地基临界荷载

一般土力学教材中的临界荷载计算公式都是在条形均布荷载、均质地基等假定条件下推得的，且在公式推导简化过程中假定了土的静止土压力系数K0＝1，即将自重应力场视为静水应力状态。显然，这种假定与大多数土的实际K0值（K0＝0.35～0.80）相差较大。假设K0＝1会过高地估计地基承载力。基于上述情况，一些学者在文献［2－5］中借助莫尔－库仑强度理论，重新“推导”了K0≠1条件下的地基临界荷载计算公式，但其“推导”中采用数学近似公式≈0.96A＋0.37B误差较大（其中A表示某点处正应力差的一半，B表示某点处的剪应力）。依据莫尔应力圆知：B≤A，通过数值分析最大误差出现在A＝B时，此时则采用该公式计算值1.414A与精确值1.33A的误差最大为6.0%（＞5.0%），误差稍大，因此其“推导”得出的公式不严密，这也导致了不同学者［4－5］推导出的公式也不一样，但推导思路及主要过程完全一致。基于此，本文采用严密的数学理论对静止侧压力系数K0≠1时的地基临界荷载进行了推导，并将本文成果应用于基础下卧软弱层的承载力验算中。

1.1 K0≠1时的地基临界荷载分析

设基础宽度为b（m）；埋深为d（m）；均布条形荷载p作用在基底；基础埋深d范围内土层平均容重为γ0；基础下土层容重为γ；其抗剪强度参数为c，φ；土的静止土压力系数为K0。

基底附加应力p为地基土中任意点的附加应力与考虑静止土压力系数K0时的地基自重应力之和，即得基底下任意点的总应力为

式中：参数角α为计算点与条形地基基底两端连接之间的夹角（°），参数角δ为计算点与条形地基底中点的连线与竖向之间夹角（°）；参数z为计算点至基底的竖向距离。

令p0＝p－γ0d，依据莫尔应力圆可求地基底任意点的主应力，若该点处于塑性区边界上，则根据Mohr－Coulomb屈服准则，该点的大、小主应力满足以下关系：

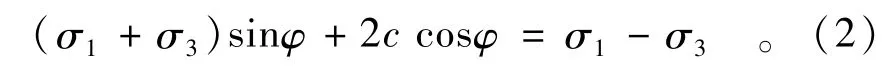
依据公式（1）、莫尔应力圆主应力计算公式及Mohr－Coulomb屈服准则，可得基底下土体处于塑性区的应力条件式，通过整理，并对塑性区深度z关于张角α求导，并令d z／dα＝0，可得α＝π／2－φ，以下塑性区深度d与p0之间关系式为

由余弦三角差公式，即：cos（α＋2δ）cos（2α＋2δ）＋sin（α＋2δ）sin（2α＋2δ）＝cosα，参考文献［3］，取α＋2δ＝π，代入上式（6）可知：

取塑性区深度为zmax＝b／4，则得由塑性区开展深度得到的地基承载力特征值为

地基的静止土压力系数K0计算采用由Jaky［2］提出并简化的公式K0＝1－sinφ，其中φ为相应土层的内摩擦角。当K0＝1时，该公式与国标5.2.5条中的公式完全一致，其中对于地基宽度b＞6 m，取6 m，对于砂土＜3 m，取3 m，该公式对相对偏心距e／b＜0.033时适用，其中各参数同上文。

1.2 考虑K0≠1时地基临界荷载与规范推荐公式的对比分析

为了分析荷载埋深对地基临界荷载的影响，取γ0＝γ，K0＝1－sinφ，将本文公式（5）与国标公式（5.2.5条）的相应无量纲公式的比值关系作为新函数（将公式（5）两边除以γb，简化为无量纲关系式），其比值关系与相对凝聚力c／γb、土的内摩擦角φ、相对埋深d／b之间关系曲面见图1。由图1可知：基础相对埋设深度越大、下层土内摩擦角越大、下层土凝聚力越小，本文导出的承载力公式与国标公式相差越大，且下层土内摩擦角影响最大。可见，考虑静止土压力系数K0≠1时临界荷载会减小，与文献［3］，［5］等结论一致，且文献［3］中图5、图6曲线特性也与本文曲面中的曲线族基本吻合。

图1 K0≠1时临界荷载（p1／4）与国标公式（5.2.5条）比值关系曲面Fig.1 Curved surfaces formed by critical load ratio（ratio of critical load in the proposed formula to that in the code formu la），and relative cohesion and internal friction angle（K0≠1）

2 对基底软弱下卧层临界埋深的探讨

2.1 规范对基础存在下卧软弱层时的承载力验算

当浅基础受力层范围内存在软弱下卧层时，国标中5.2.7条规定：当地基受力层范围内有软弱下卧层时，见图2，应按以下公式验算其地基稳定性

式中：pz为相应于荷载效应标准组合时，软弱下卧层顶面处的附加压力值；pcz为软弱下卧层顶面处土的自重压力值；faz为软弱下卧层顶面处经深度修正后的地基承载力特征值。对于条形基础式中pz值可按国标中公式（5.2.7.2条）计算，即

式中：b为条形基础底边的宽度；pc为基础底边处自重应力值；z0为基础底边面至软弱下卧层顶面的距离；θ为地基压力扩散线与垂直线的夹角，按规范表5.2.7条计算。

对于软弱下卧层容许承载力，国标5.2.5条给出了根据土的抗剪强度指标确定地基承载力特征值的计算公式（5.2.5条），该公式其实是本文K0＝1的特例。

2.2 对基础下卧软弱层临界埋深的讨论

对软弱下卧层承载力特征值的计算采用本文考虑静止土压力系数K0≠1时计算公式（5）。假设地基软弱下卧层顶面至地面深度为H（m），基底宽为b（m），地基埋深深度为d（m）；设淤泥层的重度为γ1，内摩擦角为φ1，凝聚力为c1，静止土压力系数K01＝1－sinφ1；设上部土层的重度为γ，内摩擦角为φ，凝聚力为c，静止土压力系数K0＝1－sinφ1，则地基下的软弱下卧层承载力特征值为

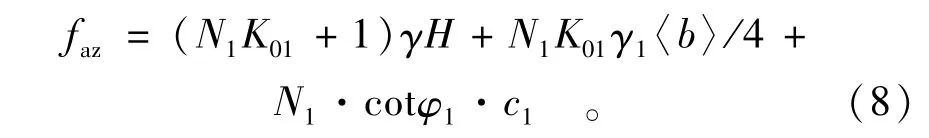
当基础埋设太深以至于接近软弱层时，承载力反而降低，故存在一个合适的埋深，使得基础不考虑软弱下卧层时的承载力与考虑软弱下卧层影响时的承载力刚好相等，即满足

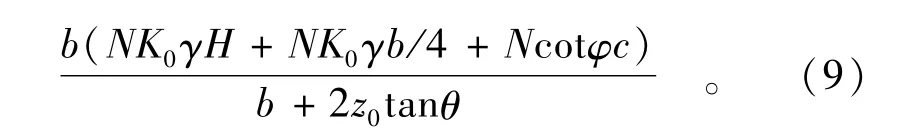
其中：参数θ按规范表5.2.7计算；Nh为上部土层的承载力参数。

对公式（9）中参数无量纲化，即对承载力等力参数乘以（1／γb），对深度、宽度等长度量乘以（1／b），将以上方程无量纲化，即：¯z＝z／b，¯H＝H／b，¯d＝d／b＝（H－z）／b，¯c1＝c1／γb，¯c＝c／γb。

通过公式（9）可知，基础相对埋深¯d和软弱层相对埋深¯H之间的函数，即当地基相对埋深控制在小于¯d时，则通过上式可求出相应的软弱层临界埋深¯Hcr（即当软弱层埋深大于¯Hcr时，可不考虑该软弱下卧层对地基的不利影响）。

求解公式（9）的无量纲化公式得

已知：地基的相对埋深深度为d／b，上部土层的重度为γ，内摩擦角为φ、凝聚力为c，静止土压力系数为K0，软弱淤泥层土的力学指标容重为γ1，内摩擦角为φ1，凝聚力为c1，静止土压力系数为K01，则依据本文公式（10），可求出软弱下卧层相对临界深度¯Hcr。即，若软弱层无量纲埋深（H／b）大于临界埋深值¯Hcr时，可不考虑软弱层对地基承载力的不利影响；反之，若软弱层无量纲埋深（H／b）小于临界埋深值¯Hcr时，则必须依据规范“5.2.7条”考虑软弱层对地基承载力的不利影响，必要时采用加大基础底宽或采用基础处理等其它措施。

图2 浅基础下存在软弱下卧层临界埋深分析Fig.2 Schematic of critical embedded depth of weak substrata under shallow foundation

3 算例分析

为了分析基础相对埋深¯d＝d／b和软弱下卧层相对临界埋深¯Hcr＝Hcr／b之间的关系，本次计算取软弱下卧层为浙江沿海地区海堤围区内的2种典型淤泥土参数：①淤泥土1＃：c1＝9 kPa，γ1＝16.5 kN／m3，φ1＝1°；②淤泥土2＃：c1＝13 kPa，γ1＝17 kN／m3，φ1＝3°。

取2种典型的地基上层土，其力学参数分别为：①上层土为黏土时，c＝30 kPa，γ＝19 kN／m3，φ＝10°；②上层土为砂土时，c＝7 kPa，γ＝18 kN／m3，φ＝23°；取地基宽度分别为2，4，6，8 m，取Es／Es1＝3，即基底压力扩散角取θ＝23°，其中静止土压力系数均取K0＝1－sinφ。采用本文理论及公式分析计算，软弱下卧层临界埋深与土层力学性质及基础底宽的关系曲线见图3。

图3 当基础底宽b＝3，6 m时软弱层相对临界埋深¯Hcr与基础相对临界埋深¯d关系曲线Fig.3 Curves of relative critical embedded depth of weak strata vs.relative critical embedded depth of foundation（foundation bottom w idth b＝3 m and 6 m）

通过实例计算分析，得出了不同基础宽度、不同土层抗剪强度指标组合下的软弱下卧层相对临界埋深¯Hcr关系曲线，认为软弱层抗剪强度指标越好、上层土内摩擦角越大，软弱下卧层相对临界埋深¯Hcr就越小，其不利影响就越小；基础底宽越大，其软弱下卧层相对临界埋深¯Hcr就越小，但当基础宽度大于6 m后，基础宽度影响逐渐变小。最后给出了软弱下卧层影响的推荐相对临界埋深值，见表1。

表1 不考虑软弱下卧层影响时的相对临界埋深¯Hcr建议表Table1 Recommendations of relative critical embedded depth when the im pact of weak substrata is not considered

4 结 语

本文采用严密的数学理论，推导了地基承载力公式；并利用该公式对基础软弱下卧层临界埋深进行深入研究，主要得出以下结论：

（1）推导了考虑静止土压力系数K0≠1时的条形地基的弹塑性临界荷载P1／4，并与国标公式5.2.5条进行了对比分析，认为国标公式高估了地基的承载力，本文公式相对较合理；基础相对埋设深度越大、下层土内摩擦角越大、下层土凝聚力越小，则本文导出的承载力公式与国标公式相差越大，且下层土内摩擦角影响最大。

（2）对基础下软弱下卧层相对临界埋深进行了研究，得出了软弱下卧层相对临界埋深¯Hcr与基础相对埋深（d／b）之间的无量纲公式。

（3）通过工程实例计算，得出了不同基础宽度、不同土层抗剪强度指标组合下的软弱下卧层相对临界埋深¯Hcr关系曲线，认为软弱层抗剪强度指标越大、上层土内摩擦角越大，则软弱下卧层相对临界埋深¯Hcr就越小，软弱下卧层的不利影响就越小。随着基础底宽越大，其软弱下卧层相对临界埋深¯Hcr就越小，但当基础宽度大于6 m后，基础宽度影响逐渐变小。最后给出了软弱下卧层影响的推荐相对临界埋深值。

［1］ GB50007—2011，建筑地基基础设计规范［S］.北京：中国建筑工业出版社，2011.（GB50007—2011，Code for Design of Building Foundation［S］.Beijing：China Building Industry Press，2011.（in Chinese））

［2］ 赵树德.地基弹塑性承载力K0≠1时的计算公式［J］.西安建筑科技大学学报，1995，27（3）：294－298.（ZHAO Shu-de.Formula of Bearing Capacity of Subgrade with K0≠1.0［J］.Journal of Xi’an University of Architecture＆Technology，1995，27（3）：294－298.（in Chinese））

［3］ 陈乐意，李镜培，梁发云.考虑荷载埋深与K0变化的地基临界荷载［J］.岩土工程学报，2010，32（12）：1930－1934.（CHEN Le-yi，LIJing-pei，LIANG Fa-yun.Critical Load of Ground Considering Load Embedded Depth and Variation of K0［J］.Chinese Journal of Geotechnical Engineering，2010，32（12）：1930－1934.（in Chinese））

［4］ 梅 岭，梅国雄，易宗发.K0≠1时的地基临塑载荷和临界载荷近似计算公式［J］.计算力学学报，2010，27（6）：1090－1095.（MEI Ling，MEI Guo-xiong，YI Zong-fa.Approximate Formulas of Critical Edge Pressure and Critical Load of Subsoil with K0≠1［J］.Chinese Journal of Computational Mechanics，2010，27（6）：1090－1095.（in Chinese））

［5］ 隋凤涛，王士杰，马建超.新的临界荷载计算公式［J］.河北农业大学学报，2009，32（5）：94－97.（SUIFengtao，WANG Shi-jie，MA Jian-chao.New Formula of Critical Load of Subsoil［J］.Journal of Agricultural University of Hebei，2009，32（5）：94－97.（in Chinese） ）

（编辑：刘运飞）

Critical Embedded Depth of Foundation’s W eak Substrata W hen K0≠1

HUANG Chao-xuan，YUANWen-xi，FANG Yong-lai
（Zhejiang ProvincialWater Conservancy and Hydropower Survey and Design Institute，Zhejiang 310002，China）

Mathematical inferential reasoning was employed to obtain the critical load P1／4of strip foundation when the effect of K0≠1 was considered，and the obtained formulawas compared with formula 5.2.5 in Code for Design of Building Foundation（GB50007—2011）.It’s believed that the formula in the Code overestimates the foundation’s bearing capacity while the formula in this study ismore reasonable.When weak substrata exists in the foundation’s load carrying layers，a check formula for the bearing capacity of theweak substrata is given in“5.2.7”in the Code，but the Code doesn’t explain under what embedded depth ofweak strata the effect of K0≠1 can be ignored.On the basis of the obtained formula of foundation’s bearing capacity，the relationship between the relative critical embedded depth（Hcr／b）ofweak strata and the relative embedded depth of foundation（d／b）was obtained through dimensionless calculation.Finally through calculation examples，curves of relative critical embedded depth（Hcr／b）with different foundation widths and different shear strengths ofweak layer were acquired.It’s concluded thatwhen the shear strength ofweak strata and the internal friction angle of topsoil are larger，the relative critical embedded depth of weak substrata Hcris smaller，hence the adverse impactwould be smaller.

foundation’s bearing capacity；coefficient of lateral earth pressure；weak substrata；critical depth of weak strata；

TV223.2；TU470.3

A

1001－5485（2013）01－0056－05

10.3969／j.issn.1001－5485.2013.01.011

2011－11－22；

2012－03－08

黄朝煊（1983－），男，湖北黄石人，硕士研究生，主要从事水工结构工程研究，（电话）13819483276（电子信箱）516227811＠qq.com。