Hybrid FEM-FIPWA for Scattering from Complex Bodies of Revolution
RUI Xi ,HU Jun,LIU Qing-huo
(1.Southwest China Institute of Electronic Technology,Chengdu 610036,China;2.School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 610054,China;3.Department of Electrical and Computer Engineering,Duke University,Durham,NC 27708,USA)
1 Introduction
The electromagnetic problem for bodies of revolution(BOR)of arbitrary shape with different kinds of materials has been widely discussed for several decades[1-6].In thiswork,FEM-BI is presented to analyze the scattering of BORwith inhomogeneousmaterials,and extend the fast inhomogeneous plane wave algorithm to accelerate the computation of the method of moment(MoM).Finite Element Method(FEM)is used to analyze the interior electric field.Edge-based and node-based elements are used to represent the interior electric field.While for the exterior region,Boundary Integration(BI)is used as a exact boundary condition.Triangular and pulse basis functions are used to represent the electric and magnetic fields on the boundary.The aggregation and disaggregation factors in Fast Inhomogeneous Plane Wave Algorithm(FIPWA)can be derived analytically.Both the memory requirement and the CPU time are saved for large scale BOR prob-lems.Numerical results are given to demonstrate the validity and the efficiency of the presented method.
2 FEM-FIPWA for Axisymmetric Resonators
2.1 Body of revolution
Because of the symmetry of the geometry,the volume of the BOR is generated by revolving a plane curve about the z-axis as shown in Figure 1.Here(ρ, ,z)are the variables in cylindrical coordinate system,θincis the angle of incident wave, t and are the unit vectors,S is the surface of the BOR.
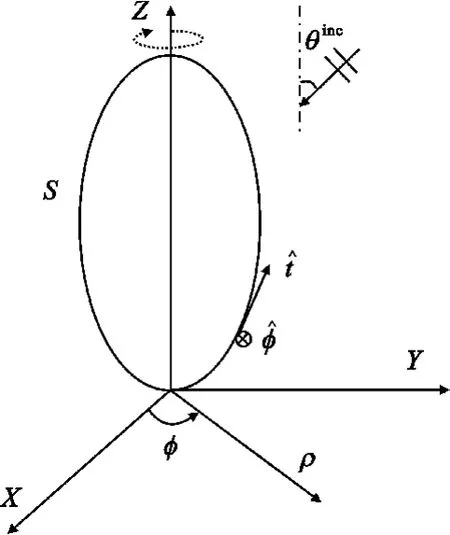
Fig.1 Body of revolution and coordinate system图1 旋转体结构坐标系统
The electric and magnetic fields can be expressed in a Fourier series:

where Et,m,E ,m,Ht,mand H ,mare the electric and magnetic fields in the meridian plane and the azimuthal component of the m-th Fourier mode,respectively.As the fields are decomposed into two parts as shown in E-quation(1-2),only a 2-D mesh(meridian cross section)is needed for analyzing the 3-D axisymmetric problem.These different modes can be treated separately because of the orthogonality.In the cylindrical coordinate system,the unit vectors t and are defined as where θ is the angle between the z-axis and the unit vector t. is the azimuthal angle as shown in Figure 1.

2.2 FEM for the interior region
As shown in Figure 2,the interior region of the BOR is filled with inhomogeneous material with the relative permittivity εrand the relative permeability μr.Both εrand μrare the functionof z and ρ,but independent of .

Fig.2 The mesh for the interior and exterior regions图2 内部区域与外部区域的网格划分
The vector Helmholtz equation for the electric field can be written as

where Seis the source term,and k0is the wave number in free space.If it is source free(Se=0)in the interior region the weak form of the vector wave equation can be expressed as[7-8]
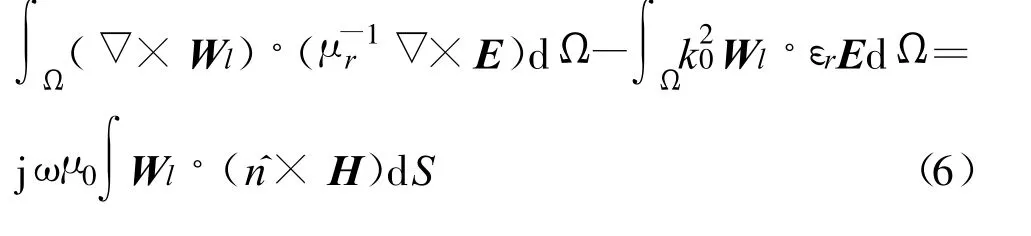
where Wlis the testing function,and μ0is the permeability of the free space.
The fields must retain the continuity for any values of on the z-axis(ρ=0).Thus,there are three kinds of conditions for different cylindrical modes:

The basis functions for the electric field are chosen as

where Nnis the number of nodes,Nsis the number of segments(or edges),et,iand e,iare the unknown coefficients,and Niand Nirepresent the standard node-based and edge-based element basis functions,respectively.The magnetic field on the boundary S is expanded as the same as the electric field.

The testing function is chosen as
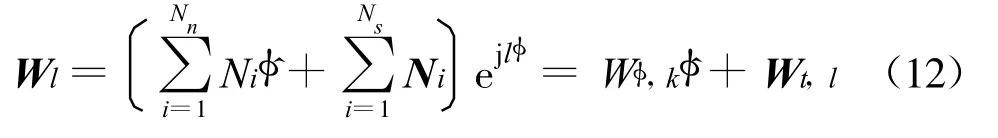
After substituting the basis and testing functions into Equation(6)and making use of the orthogonality of cylindrical modes,the wave equation can be rewritten as

can be formed,where m is the index of the mode and b is the index of boundary.And the matrix element can be expressed as

where αand β are the choices for the testing function and the basis function.et=(et,1,et,2,…,et,Ns)T,e =and.K is the total number of the elements,Kbis the number of the boundary elements.
A seven-point numerical integration is used for the impedance matrix assembling.The unknowns contain six parts,the interior electric fieldand,the boundary electric fieldand,the boundary magnetic fieldand.The matrix equation for FEM part can be rewritten as

2.3 FIPWA for the exterior region
For the exterior region,boundary integration is applied to govern the boundary electricfield E and magnetic fields M.The fieldson the boundary S can be written as

where J and M are the equivalent electric and magnetic currents,which will satisfy the electric field integral equation(EFIE)and the magnetic field integral equation(MFIE)
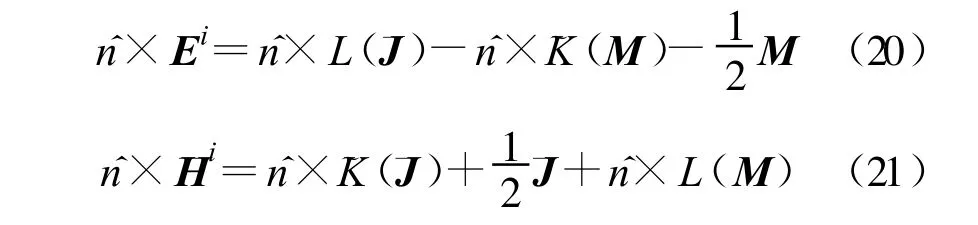
where Eiand Hiare the incident electric and magnetic fields, Hi=η0Hi, J=η0J,η0is the wave impedance in the free space,L and K are the operators which can be expressed as

where G is the Green′s function,and the integration in the equation above has remove the contribution of the singular point.The key process of MoM is solving the modal Green′s function gnwhich can be expressed as

For the traditional MoM,the modal Green′sfunction has to be evaluated by numerical method,hence it is time consuming when the radius of the BOR is large.In this section,fast inhomogeneous plane wave algorithm(FIPWA)is applied to accelerate the computation of the MoM for bodies of revolution.Based on Weyl Identity[9-10],the Green′s function can be expressed as
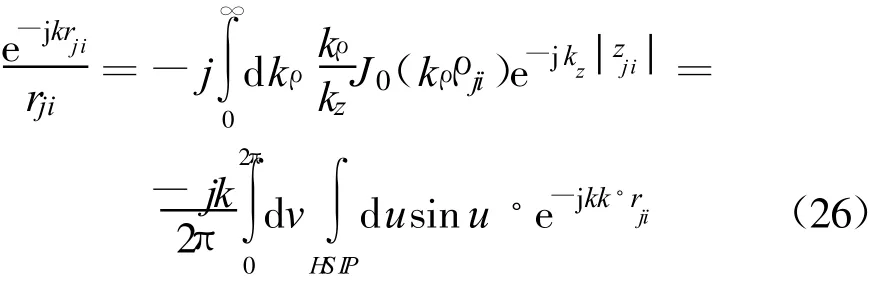
where k=k( xsinucosv+ ysinusinv+ zcosu),kρ=ksinu,kz=kcosu,rji=rj-ri.Here riis the source point and rjis the field point.In the following part,they are also named sub-scatterers.The integration of the variable u in Equation(26)is computed along the half Sommerfeld integration path(HSIP)in Figure 3.Equation(26)can be viewed as the summation of the inhomogeneous plane waves in different directions,which are expressed by k(u,v),and weighted by sinu.
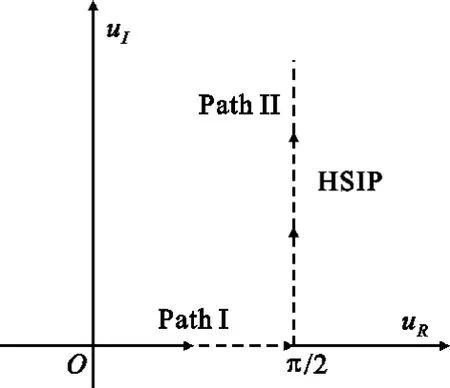
Fig.3 The Sommerfeld integration path on the complex u plane图3 复平面上的Sommerfeld积分路径
In order to realize the Fast Inhomogeneous Plane Wave Algorithm(FIPWA),the basis functions are divided into groups.Here we call rmand rm′are the centers of the groups which contain the source point rjand field point rirespectively.As shown in Figure 4,rji=rjm+rmm′+rm′i.Equation(26)can be rewritten as


Fig.4 The field point and the source point图4 场点与源点位置分布
The basis functions are divided into M groups along the z direction as shown in Figure 5.In this way,the factor rmm′has z component only.This character will make the integrand decay exponentially away from the real axis in the complex u plane.

Fig.5 The BOR is divided into groups图5 旋转体分组示意图
Equation(26)can be rewritten as

where

Here the Bjm(u,v)and Bm′i(u,v)represent the radiation and receiving patterns for the field and source groups,respectively.And f(u)can be considered as the weight function.Both Bjm(u,v)and Bm′i(u,v)are the inhomogeneous plane wave as u is complex.With proper numerical methods for u and v,the integral can be expressed as
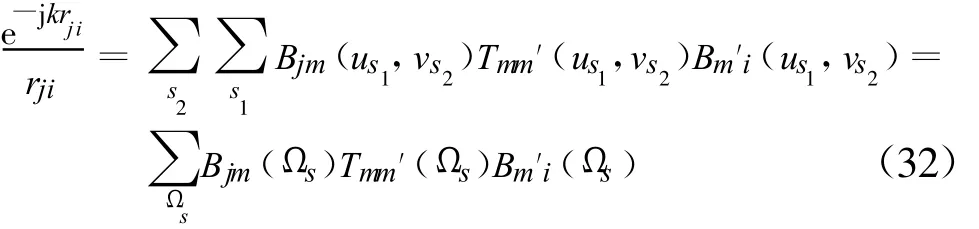
where

The detail of the FIPWA can be found in Reference[5-6].
2.4 FEM-FIPWA for BOR
The currents J and M are defined as

where Piis the pulse basis function and Tiis the traditional triangle basis function.Combining the FEM part(interior region)and FIPWA(boundary),the matrix equation can be derived as

The details of the matrix elements can be found in Reference[4-6].The boundary currents and fields can be derived by solving the equation above,and the far field also can be solved.In the next section,two numerical results will be given to demonstrate the validity and the efficiency of the proposed method.
3 Numerical Results
In this section,two numerical results are presented to show the validity of the proposed FEM-FIPW A method.All problems are solved on the same computer(Intel Core2 DuoCPU P8400@2.26GHz with 1.92 GB RAM)in order to make a fair comparison,with only one core being used.
3.1 An inhomogeneous dielectric sphere with two layer medium
As shown in Figure 6,an inhomogeneous dielectric sphere is computed.The sphere isexcited by the plane wave with horizontal polarization(θinc=00,inc=00,λ=2 m).The total number of the unknowns is about 40 000.The bistatic RCS is shown in Figure 7,the result of FEM-BI(or FEM-FIPW A)agreeswell with analytical result.

Fig.6 An inhomogeneous dielectric sphere with two-layer medium图6 非均匀双层介质球结构
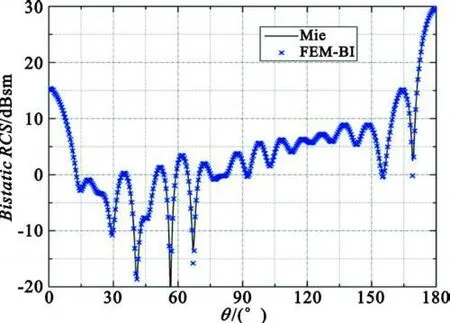
Fig.7 The bistatic RCS of the dielectric sphere result by FEM-BI compared with analytic result图7 介质球双站RCS的计算结果比较图
3.2 An inhomogeneous dielectriccylinder
The numerical result proposed above shows the accuracy of FEM-FIPWA for BORproblems.In this section,a more complex example is shown to verify the efficiency of proposed method mentioned in this paper.As shown in-Figure 8,there are seven layered medium.The thickness of the six inner medium is 0.2 m and the height is 2.6 m.The thickness of the outer medium is0.3 m,and the height is 2 m.The cylinder is excited by the plane wave with horizontal polarization(θinc=90°,inc=0°,λ=0.5 m).The number of the total unknowns is more than 100 000 in this 2-D mesh.The field distribution derived by FEM-BI is compared with Wavenology which is a famous commercial EM software in USA.As shown in Figure 9,the results agree well with each other.

Fig.8 The geometry of the inhomogeneous dielectric cylinder图8 非均匀介质柱结构图

Fig.9 The field distribution of the dielectric cylinder with two different methods图9 两种方法计算介质柱的场分布结果比较
As shown in Table 1,the memory requirements and CPU times for FEM-MoM and FEM-FIPWA are compared.

Table 1 The comparison between FEM-MoM and FEM-FIPWA表1 FEM-MoM与FEM-FIPWA计算比较
4 Conclusion
In this paper,hybrid FEM and FIPWA technique is applied to solve the BOR scattering problem.In this FEM-FIPWA method,the problem is separated into interior and exterior problems.In the interior region,FEM based on hybrid edge-based and node-based elements is used to present the electric field.In the exterior region,boundary integration(BI)is used as the exact boundary condition.Triangular and pulse basis functions are used for representing the electric and magnetic fields on the boundary.FIPWA is added for the BI part.The proposed method can solve large scale bodies of revolution with inhomogeneous,composite materials efficiently.
[1] Andreasen M G.Scattering from bodies of revolution[J].IEEE Transactions on Antennas and Propagation,1965,13(2):303-310.
[2] Mautz J R,Harrington R F.Electromagnetic coupling to a conducting body of revolution with a homogeneous material region[J].Electromagnetics,1982(2):257-308.
[3] Medgyesi-Mitschg L N,Putnam JM.Electromagnetic scattering from axially inhomogeneousbodies of revolution[J].IEEETransactions onAntennas and Propagation,1984,32(8):797-806.
[4] Rui Xi.Finite element methodfor inhomogeneous axisymmetric resonators[J].Telecommunication Engineering,2012,52(1):105-110.
[5] Rui X,Hu J,LiuQ H.Fast Inhomogeneous Plane Wave Algorithm for Scattering from PECBody of Revolution[J].Microwave and Optical Technology Letters,2010,52(8):1915-1922.
[6] Rui X,Hu J,Liu Q H.Higher order finite element method for inhomogeneous axisymmetric resonators[J].Progress In Electromagnetics Research B,2010,21:189-201.
[7] MorganM A,Mei K K.Finite-element computaion of scattering by inhomogeneous penetrable bodies of revolution[J].IEEE Transactions on Antennas and Propagation,1979,27(2):202-214.
[8] Lee J F,Wilkins G,Mittra R.Finite-element analysis of axisymmetric cavity resonator using a hybrid edge element technique[J].IEEE Transactions on Microwave Theory Technique,1993,41(11):1981-1987.
[9] Chew W C.Waves and Fields in Inhomogeneous Media[M].New York:Van Nostrand Reinhold Co.Ltd.,1990.
[10] Hu B,Chew W C,Michielssen E,et al.Fast inhomogeneous plane wave algorithm for the fast analysis of two-dimensional scattering problem[J].Radio Sciences,1999,34(4):759-772.

