基于压缩感知观测序列的语音信号基音周期提取*
曹 杨
(南京邮电大学通信与信息工程学院,南京 210003)
压缩感知(Compressed Sensing,CS)理论是2004年由 D.Donoho、E.Candès等人提出的,它突破了传统奈奎斯特采样定理对采样率与信号带宽之间的约束关系,实现对信号的边采样边压缩,用更少的采样数据量来恢复原始信号。当信号在某个域满足稀疏性,且感知矩阵满足RIP(Restricted Isometry Property)特性时,信号能够被以大概率精确重构。文献[1-2]指出语音信号在多个域满足稀疏性条件,若能利用更少的信号量来提取原始信号的各种特征,将大大减少计算量。本文主要研究将压缩感知技术应用于语音信号并从观测序列中直接提取基音周期的技术。
1 压缩感知的数学模型
设N维信号 X∈RN×1由某组正交变换基表示成如下形式:
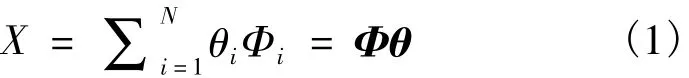
其中 θi=〈X,Φi〉,即

式中,Φ∈N×N的正交变换矩阵,若θ是K稀疏的,即θ中非零元素个数为K(K<<N),则可以采用另一个与Φ不相关的矩阵Ψ∈RM×N(M<N)对θ进行压缩观测,得到观测序列

Ψ称为投影矩阵,令ΨΦT=Θ,则
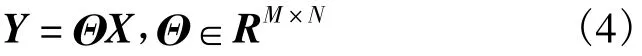
称Θ为观测矩阵。当Θ满足RIP特性,可以在接收端从M=O( Klg(N))个观测值中以高概率重构原始信号,方法为解凸优化问题:
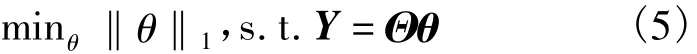
由上述模型可知,压缩感知的观测序列长度M小于原始信号长度N,将N/M定义为压缩比r(r>1)。
2 检测方法设计
2.1 压缩感知稀疏基及投影矩阵的选择
本文主要研究上面模型中的观测序列Y,在不重构原始信号的情况下,从Y中提取基音周期。文献[3]CS理论中指明信号的稀疏性越好,其重构误差越小,文献[4]表明语音信号在离散余弦(DCT)域稀疏性较好,本文采用DCT基作为稀疏变换基。
CS中常用的投影矩阵可分为两类,即确定性和非确定性投影矩阵。利用非确定性投影矩阵(如高斯随机矩阵)投影得到的观测序列呈现类似白噪声特性,不能体现浊音信号的周期性;文献[5]提出的行阶梯矩阵是一种确定性投影矩阵,在DCT基下满足RIP特性,可以用于语音的压缩感知。实验发现基于行阶梯投影矩阵的观测序列仍保留了原始浊音信号的周期性,所以本文选用行阶梯矩阵作为投影矩阵。下文中提到的观测序列均为行阶梯投影下的观测序列。图1为一帧纯净语音浊音段在行阶梯和高斯投影矩阵下的观测序列的对比(r=2)。由图1可以看出,浊音段在行阶梯矩阵下的观测序列也呈现与原始语音信号同样的周期性,周期为原始信号的
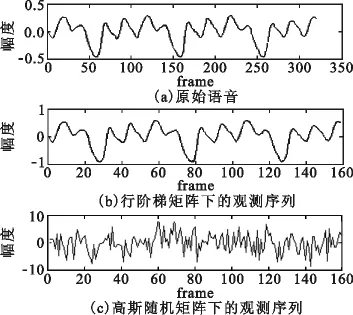
图1 行阶梯与高斯随机矩阵下的观测序列Fig.1 Compressed sensing sequence under row echelon matrix and Gaussian random matrix
2.2 小波变换
语音信号是一种短时平稳信号,文献[6]说明原始语音信号含有噪声时,通过选择合适的小波基和变换尺度可以将语音与噪声有效地分离。小波变换的低频系数对应着语音信号的低频分量(包含大部分信号能量),小波变换的高频系数对应语音的高频分量及噪声。
基音为低频信号,由图1可以看出语音信号观测序列仍保留了原始信号的大部分波形,因此可以考虑对观测序列进行小波分解,对低频系数提取基音周期。
2.3 清浊音辨别
清音帧的观测序列经小波分解后其系数与浊音帧存在一定的差异,浊音帧的能量分布主要集中在低频部分,而清音帧的能量分布比较均匀,因此可以将小波子带的能量大小作为清浊音辨别的标准。为使清浊音判别更加准确,在使用子带小波能量作为第一个判别参数后,引入观测序列的短时过零率作为第二个判别参数。具体方法如下:首先对每帧语音信号的观测序列做j级小波变换,得到j+1个子带,计算各子带能量。若用Ei表示第i个子带的能量,E1为最低频子带能量,Ej+1为最高频子带能量,计算低、高频子带能量比:

计算该帧的短时过零率ZCR,若t大于某个门限值TH1且ZCR小于某个门限值TH2,则认为该帧为浊音帧,否则为清音帧。TH1由大量实验获得,本文中取为1,TH2取该段语音各帧过零率的中值。
2.4 基音周期检测
目前最常用的基音周期检测算法为短时自相关函数法,其定义为
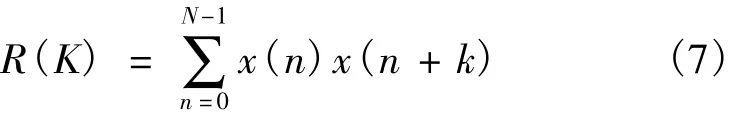
其中,N为语音信号加窗分帧时的窗口长度,由式(7)测得浊音信号的自相关函数的峰值与峰值之间的距离即为基音周期。但当语音信号含噪时,对浊音信号的周期性产生一定影响,从而极大地影响了提取基音周期准确率。将含噪语音进行小波分解后,将低频小波系数看做消噪后的语音信号可以大大减小噪声影响。
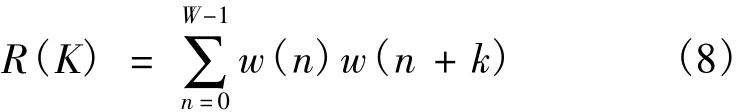
其中,w(n)是小波分解后低频小波系数的第n个值,W为低频小波系数总个数。测得R(K)相邻两峰值间的距离d。W为观测序列长度的,R(K)的峰值出现位置是直接对观测序列求自相关时,其自相关函数峰值位置的倍。
基于上述分析,本文具体算法步骤如下:
(1)含噪语音信号分帧,抽样频率为16 kHz,每帧320个样点,进行压缩感知,压缩比为r,得到每帧的观测序列;
(2)用db1小波对每帧观测序列进行j(j=2)级小波分解;
(3)清浊音判别,计算各子带能量及该帧短时过零率 ZCR,由式(6)计算 t,t>TH1且 ZCR <TH2,则判为浊音,否则为清音;
(4)对清音帧,基音周期设为0,对浊音帧由式(8)分别计算出R(K),测得R(K)相邻两峰值间的距离d,则该帧的基音周期为2jrd。
3 实验仿真与结果分析
下面分别对一段男声和女声采用本文方法进行基音周期检测。
当压缩比r=2,原始信号中混入高斯白噪声时,图2、图3、图4分别为信噪比(SNR)为5 dB、0 dB及-5 dB时的基音周期轨迹图。
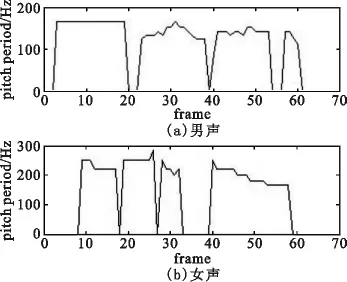
图2 r=2、SNR=5 dB时男女声的基音轨迹Fig.2 Male and female pitch tracks under r=2,SNR=5 dB

图3 r=2、SNR=0 dB时男女声的基音轨迹Fig.3 Male and female pitch tracks under r=2,SNR=0 dB
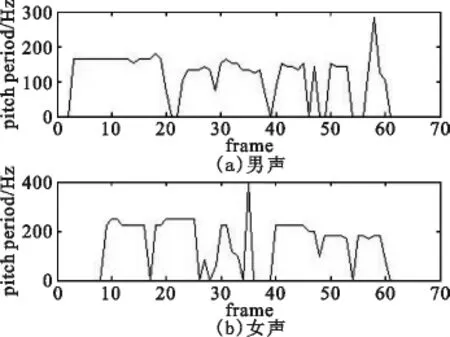
图4 r=2、SNR=-5 dB时男女声的基音轨迹Fig.4 Male and female pitch tracks under r=2,SNR= -5 dB
表1给出了r=2时不同信噪比下本文所提方法与传统自相关方法的准确度的对比。实验采用3句男声和3句女声语音,使用Praat语音分析软件和手工标注的方法得到标准基音周期,当实验获得的基音周期与标准相差10%时,认为检测出错。
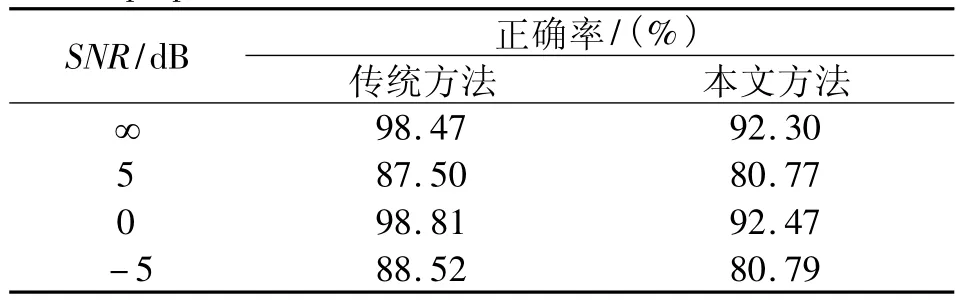
表1 r=2时不同信噪比下传统方法与本文方法检测正确率Table 1 The correct rate to detect using traditional and proposed method under different SNR with r=2
由表1可以看出,本文所提算法与传统方法检测的正确率相当。下面分析传统方法与本文方法的计算量。
对一帧浊音信号(N个样点)提取基音周期,由公式(7)传统自相关方法所需要的计算量为N2/2次乘法、N2/2-N次加法。
文献[7]中指出不使用快速算法时小波分解的计算量为2N次乘法、2(N-1)次加法,由本文所提方法对一帧浊音信号的观测序列(r=2时共N/2个观测值)首先进行2级小波分解所需计算量为3/2 N次乘法、3/2(N-1)次加法,2级小波分解低频系数共N/8个,计算其自相关所需计算量为N2/64次乘法、(N2/64-N/8)次加法。因此使用本文方法计算一帧浊音信号的计算量为(N2/64+3/2N)次实乘、(N2/64+3/2(N-1)-N/8)次实加。由以上分析可知本文算法的计算量比传统方法大大减少。
4 结束语
本文对语音信号压缩感知的观测序列进行了研究,提出了一种直接从观测序列中提取基音周期的方法。对行阶梯投影矩阵下的观测序列通过小波分解得到低频小波系数,对低频小波系数求自相关,测得基音周期。仿真实验表明,本文所提方法与传统(非压缩感知)方法检测结果的准确度和抗噪性相当,但本文所提方法的计算量大大减少,对实际工程有重大参考价值。本文也发现了有待研究的问题,即可寻找比行阶梯矩阵更优的其他观测矩阵,可以更好地保留原始信号的结构性特征。
[1] 叶蕾,杨震.基于压缩感知的语音压缩与重构[J].南京邮电大学学报自然科学版,2010,30(4):57-60.YE Lei,YANG Zhen.Compression and Reconstruction of Speech Signal Based on Compressed Sensing[J].Journal of Nanjing University of Posts and Telecommunications(Natural Science),2010,30(4):57 -60.(in Chinese)
[2] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.SHI Guang-ming,LIU Dan-hua,GAO Da-hua,et al.Advances in theory and application of compressed sensing[J].Acta Electronica Sinica,2009,37(5):1070 -1081.(in Chinese)
[3] Candes E J,Wakin M B.An Introduction to Compressive Sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[4] Wu D,Zhu Wei-ping,Swamy M N S.On sparsity issues in compressive sensing based speech enhancement[C]//Proceedings of 2012 IEEE International Symposium on Circuit and Systems.Seoul:IEEE,2012:285 -288.
[5] 叶蕾,杨震,王天荆,等.行阶梯观测矩阵、对偶仿射尺度内点重构算法下的语音压缩感知[J].电子学报,2012,40(3):430-434.YE Lei,YANG Zhen,WANG Tian - jing,et al.Compressed Sensing of Speech Signal Based on Row Echelon Measurement Matrix and Dual Affine Scaling Interior Point Reconstruction Method[J].Acta Electronica Sinica,2012,40(3):430 -434.(in Chinese)
[6] Li Ru - wei,Bao Chang - chun,Dou Hui- jing.Pitch Detection Method for Noisy Speech Signals Based on Pre-Filter and Weighted Wavelet coefficients[J].Signal Processing,2008,26(9):530 -533.
[7] 徐伟业,宋宇飞,宗慧.一种基于离散傅里叶变换的小波变换的快速算法[J].南京工程学院学报(自然科学版),2005,3(1):12-17.XU Wei- ye,SONG Yu - fei,ZONG Hui.A Fast Wavelet Transform Algorithm Based on Discrete Fourier Transform[J].Journal of Nanjing Institute of Technology(Natural Science Edition),2005,3(1):12 -17.(in Chinese)
——以NHK新闻为中心

