一种利用信源冗余的Turbo均衡新算法*
乔 良,郑 辉
(盲信号处理重点实验室,成都 610041)
1 引言
根据香农的信源信道分离理论,传统通信系统中的信源编码和信道编码是独立进行设计的[1]。然而在实际应用中,由于译码延迟以及计算复杂度的约束,信源编码总是次最优的,无法完全去除信源中的冗余。信源残留冗余可以在接收端被用来提高通信系统的性能,近十多年来,利用信源冗余的联合信源信道译码受到了人们的广泛关注[2-4]。数据流中的固定字段等已知比特可以看作是信源冗余,如果能够有效地加以利用,同样有助于系统性能的提高。Cao[5]针对噪声中的图像传输问题,在传统Viterbi译码的基础上,结合固定字段提出了约束Viterbi算法,提高了系统性能。Xiang[6]提出了一种在数据流中动态检测固定字段的容错译码算法,将联合信源信道译码扩展到解调软判决处理。涂世龙等[7]研究了自同步加扰系统的联合信源信道译码问题,提出由去扰数据进行固定字段检测,得出错误位置,并进一步映射为去扰前错误位置,从而在译码之前预先纠错,以提高译码性能的容错处理方法。
在过去十多年的时间里,尽管联合信源信道译码技术得到了广泛的研究,但是大部分的研究都局限于AWGN信道,本文在无线衰落信道中考虑这一问题。在无线信道的接收处理中,为克服信道多径和衰落的影响,信道均衡技术被广泛应用,Turbo均衡通过在均衡器和译码器之间迭代交换外信息,有效改善了信号接收处理的性能,复杂信道条件下其性能较传统判决反馈均衡(DFE)有3 dB以上的提升[8-10]。本文将联合信源信道译码与Turbo均衡技术结合起来,首先提出了一种软输入软输出(SISO)的联合信源信道译码算法,利用信源中的已知比特改善译码器的性能,然后再将译码器输出的外信息反馈回均衡器,在均衡、译码、信源之间构建了软信息交互的环路,从而有效提升接收机在严重ISI信道下的误码性能。
本文的组织结构如下:第2节基于传统maxlog-map译码算法[11]提出了一种结合信源冗余的SISO卷积译码算法,第3节构建了利用信源冗余Turbo均衡的整体处理框架,第4节利用EXIT图对本文算法进行了分析,第5节给出了计算机仿真的结果,最后对全文进行总结。
2 结合信源冗余的卷积译码
文献[5]在传统Viterbi算法的基础上,结合信源冗余提出了约束Viterbi算法(C-Viterbi)。传统Viterbi算法通过在卷积码网格图中寻找最大似然(ML)度量最大的路径作为幸存路径,然后回溯幸存路径从而得到译码比特。如果信源中的若干比特是先验已知的,那么幸存路径在通过相应位置时就需要遵循这些已知比特的约束,只能通过这些比特所限定的路径,这就是C-Vitervi算法的基本思想。尽管C-Viterbi算法通过考虑信源冗余提升了译码性能,而且在一定程度上降低了译码复杂度,但是其译码输出为硬判决,并不适用于迭代处理。为了能够计算外信息,将译码软输出反馈回均衡器,本节基于传统的max-log-map译码器,提出了结合信源冗余的SISO译码算法,用于后续迭代处理。
考虑码率为R的卷积编码,R=k/n,l时刻的信息比特 ul=(ul,0,ul,1,…,ul,k-1),编码比特 vl=(vl,0,vl,1,…,vl,n-1),其中第 j个信息比特的后验概率为

式中,r表示接收比特序列,σ+表示l时刻信息比特ul,j=+1对应的所有状态对,σ-表示l时刻信息比特ul,j=-1对应的所有状态对。max-log-map译码算法中涉及到的分支度量γ、前向度量α和后向度量β分别为

式中,Lc为信道可靠度因子,当信源冗余存在时,前向度量α和后向度量β的递归计算方式完全相同,只是分支度量γ有所变化。假设l时刻,第j'个信息比特为已知的信源冗余,其值为 1,则 p(ul,j'=+1)=1,p(ul,j'= -1)=0,则 l时刻的分支度量 γl(s',s)为

当ul,j'=-1时,也有类似的结果。信息比特ul,j的后验概率为

将3种度量的计算结果代入式(6)中,就可以得到相应信息比特的软输出。
图1给出了上述结合信源冗余的max-logmap译码算法的仿真结果,仿真采用了实际中得到广泛应用的(2,1,7)卷积码,其生成多项式为(133,171),无删除。定义信源冗余的比例为η,其表示已知比特占所有信源比特的比例,η=0即为传统的max-log-map译码算法,仿真中假设信源冗余的分布是完全随机的。从图1可以看出,信源冗余给译码器性能带来的提升较为有限,在10-4误码率条件下,70%信源冗余所能带来的性能提升仍小于1 dB。

图1 结合信源冗余卷积译码算法的误码性能Fig.1 BER performance of the convolutional decoding method using residual source redundancy
3 利用信源冗余的Turbo均衡
图2给出了利用信源冗余的Turbo均衡的处理流程。

图2 利用信源冗余的Turbo均衡处理流程Fig.2 Block diagram of Turbo equalization using residual source redundancy
在发送端,信息比特u经过编码、交织后形成待传输的比特序列 c[c1,c2,…,cL],共 L·Q 个比特,其中子序列 cn[cn,1,cn,2,…,cn,Q],cn,j∈{0,1}。星座映射模块将每个子序列cn映射为发送符号 xn∈S={α1,α2,…,α2Q},星座点 αj对应 Q 个特定的比特。对于PSK调制有
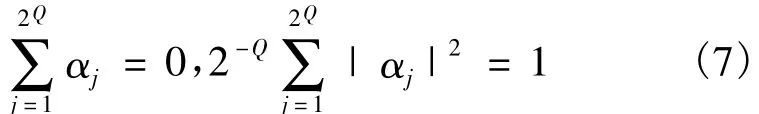
设符号间干扰信道的冲激响应为

其中,M是信道冲激响应的长度,加性噪声wn是独立同分布的复高斯随机变量,实部和虚部的方差都等于/2,则接收符号zn的表达式为
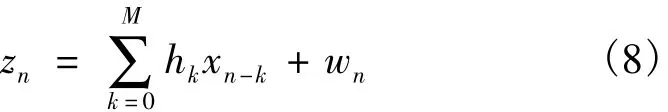
对于N=N1+N2+1个接收符号,式(8)可以表示为矩阵形式:

其中,各项的定义如下:

Turbo均衡根据其实现结构,分为最大后验概率(MAP)均衡和最小均方误差(MMSE)均衡,其中MAP均衡的运算量随着信号星座图的大小和信道冲激响应长度的增加呈指数增长,而MMSE均衡基于滤波器结构,其运算量仅与均衡滤波器长度的平方成正比,更加适合于实际应用,因此本文选用了MMSE Turbo均衡。根据文献[9],这里直接给出均衡符号的计算公式:
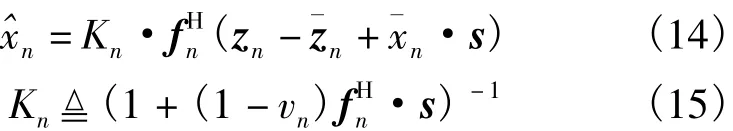
其中,fn是均衡滤波器的系数,
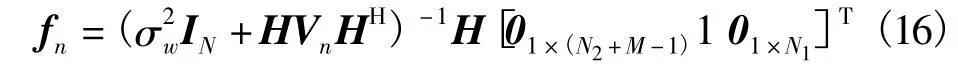
4 基于EXIT图的性能分析
外信息传递(Extrinsic Information Transfer,EXIT)图是一种半解析的分析工具,最早用于分析Turbo码的迭代译码过程,Turbo均衡提出后,很快被用于Turbo均衡的性能分析[9]。EXIT图描述了译码器输出互信息与均衡器输出互信息Ie=之间的传递关系。互信息定义为[12]
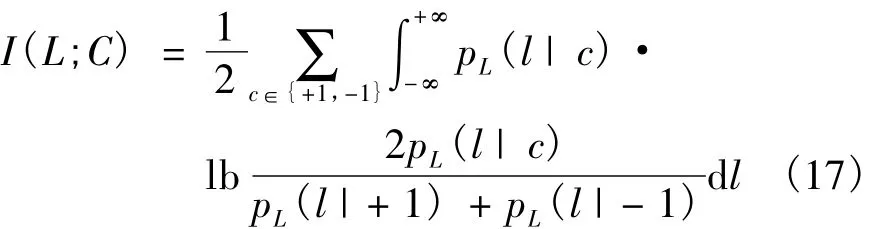
其中,pL(l|c)表示相应的发送比特为c时对数似然比(LLR)的条件概率密度函数。输入的LLR通常建模为均值为、方差为的高斯随机变量,所以

对于一个给定的σL,输入互信息可以通过数值的方式计算出来。输出LLR的条件概率密度函数一般由计算机仿真得到的直方图来近似,同样再次通过数值计算可以得到输出互信息。这样,改变σL的取值,就可以得到一组(Id,Ie)的取值,也就是EXIT图。
图3给出了在不同信源冗余度条件下,译码器的EXIT图,仿真仍然采用(2,1,7)卷积码。从图中可以看出,信源冗余的存在有效改善了译码器在较低输入互信息条件下的输出互信息。图4将译码器的EXIT图和均衡器的EXIT图显示在一张图中,Turbo均衡迭代过程在图中可以用Id→Ie和Ie→Id阶梯形的轨迹来描述。仿真中符号间干扰(ISI)信道采用文献[13]中所使用的严重ISI信道,其信道冲激响应为 h=[0.227,0.46,0.688,0.46,0.227],该信道能够充分体现均衡算法对抗ISI的性能,在相关的研究文献中得到了广泛使用,仿真信噪比范围为1.0~4.0 dB。从图中可以看出,当不考虑信源冗余(η=0)时,译码器和均衡器的EXIT曲线在Ie=0.2左右就已相交,Turbo均衡迭代无法取得更大的互信息输出。考虑信源冗余(η=0.7)之后,Eb/N0=1.0 dB时,译码器和均衡器的EXIT曲线仍相交于较低的互信息输出(Ie≈0.35),此后随着信噪比的提高,两条EXIT曲线交点的互信息迅速提升,此时对应的误码率曲线迅速下降;而当Eb/N0=4.0 dB时,交点互信息 Ie≈0.7,此时已经达到较低的误码率。
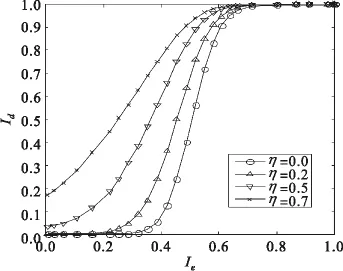
图3 不同信源冗余度条件下译码器的EXIT图Fig.3 EXIT charts of the decoder at different source redundancy ratios
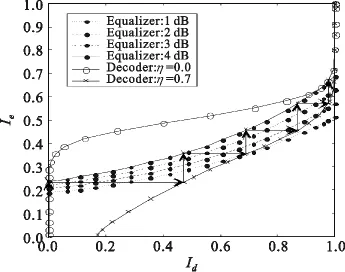
图4 结合信源冗余的Turbo均衡EXIT图Fig.4 EXIT charts of Turbo equalization using residual source redundancy
5 仿真实验
本小结采用计算机仿真的方法比较利用信源冗余的Turbo均衡与传统Turbo均衡的性能。为了方便比较,同时给出了理想AWGN(无ISI)信道下的误码性能。仿真中仍然采用(2,1,7)卷积码和第4节中的严重ISI信道,信息比特长度为1 536 b,则编码比特的长度为3 072 b,交织采用文献[14]中的S伪随机交织器,调制方式为8PSK,编码比特对应的符号数为1 024。
图5给出了不同信源冗余度条件下严重ISI信道Turbo均衡的误码性能,信源冗余度 η为0.0、0.2、0.5、0.7,分别对应从右至左的 4 条曲线,其中η=0对应传统Turbo均衡的性能。为了方便比较,同时给出了AWGN信道下的误码率。从图中可以看出,由于该信道中的符号间干扰非常严重,即使采用了Turbo均衡迭代处理算法,其性能距离理想AWGN信道(无ISI)下的误码率仍然有很大的差距。利用信源冗余后,尽管译码算法的性能提升非常有限,70%的信源冗余度,在10-4误码率时,信噪比提升小于1 dB。然而在ISI信道结合Turbo均衡之后,同样是在10-4误码率,信源冗余度为20%时,信噪比提升大于2.5 dB;信源冗余度为50%时,信噪比提升大于7 dB;信源冗余度为70%时,信噪比提升约9.5 dB。当信源冗余度为70%时,其性能已经非常接近理想AWGN信道下的误码曲线。注意到信源冗余度为70%时,Eb/N0=1.0 dB之后,误码率曲线迅速下降,Eb/N0=4.0 dB时,误码率已经达到10-4量级,这与第4节中的分析结果是一致的。
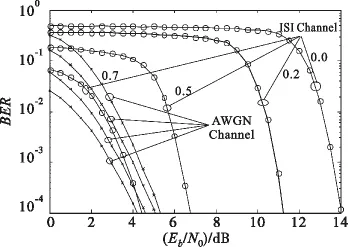
图5 结合信源冗余的Turbo均衡在严重ISI信道的误码性能Fig.5 BER performance of Turbo equalization using residual source redundancy in severe ISI channel
实际的通信系统在设计之初,通信容量总会留有一定的余量,因此系统中不可避免地具有一定比例的信源冗余。以时分复用(TDM)系统为例,相关统计[6]表明大多数 TDM系统的时隙占用率只有10% ~20%,其余部分则填充一些固定字段,系统中具有很高比例的信源残留冗余。本文所提算法在无线衰落信道的接收处理过程中充分利用了这些信源冗余,从而大大提升了系统性能,具有较高的实际应用价值。
6 结论
本文在无线衰落信道下研究了利用信源冗余,从而提高接收系统性能的方法,将联合信源信道译码技术扩展到ISI信道,并与Turbo均衡技术相结合,提出了一种新的利用信源冗余的Turbo均衡算法。该算法首先利用信源冗余提升译码器的性能,然后将性能改善后的外信息反馈回均衡器,在均衡、译码、信源之间建立起软信息交互的环路,有效提高了整体接收的性能。EXIT图分析和计算机仿真均表明,尽管信源冗余给译码器带来的性能提升较为有限,70%信源冗余对应的信噪比提升小于1 dB,但是将这部分信息反馈回均衡器后,在严重ISI信道,信源冗余度为70%时,整体接收的性能改善约为9.5 dB,基本达到了理想AWGN信道下的误码性能。
需要指出的是,虽然本文是在卷积码条件下提出了利用信源冗余的Turbo均衡算法,但是本文所提思路对于新一代无线通信中大量使用的Turbo、LDPC等编码仍然是适用的。仿真中假设信道冲激响应已知,这在实际通信系统中也可以通过利用训练序列进行信道估计和跟踪来实现。上述问题将在后续研究中进一步深入分析。
[1] Shannon C E.A mathematical theory of communication[J].Bell System Technical Journal,1948,27(3):379-423.
[2] Sayood K,Borkenhagen J C.Use of residual redundancy inthe design of joint source/channel coders[J].IEEE Transactions on Communications,1991,39(6):838 -846.
[3] Jeanne M,Carlach J C,Siohan P.Joint source-channeldecoding of variable-length codes for convolutional codes and turbocodes[J].IEEE Transactions on Communications,2005,53(1):10-15.
[4] Grangetto M,Cosman P,Olmo G.Joint source/channel codingand MAP decoding of arithmetic codes[J].IEEE Transactions on Communications,2005,53(6):1007 -1016.
[5] Cao L,Chen C.A novel product coding and recurrent alternate decoding scheme for image transmission over noisy channels[J].IEEE Transactions on Communications,2003,51(9):1426-1431.
[6] Xiang Weiwei,Lu Peizhong.Joint source channel soft decoding using dynamic redundancy detection[C]//Proceedings of 2009 International Conference on Networks Security,Wireless Communications and Trusted Computing.Wuhan:IEEE,2009:576 -579.
[7] 涂世龙,乔良,管涛.利用固定字段的自同步加扰系统容错译码[J].计算机工程与科学,2012,34(4):133-137.TU Shi- long,QIAO Liang,GUAN Tao.Error-resilient decoding in the system with self-synchronization scrambling code by utilizing constant bytes[J].Computer Engineering and Science,2012, 34(4):133 - 137.(in Chinese)
[8] Douillard C,Jezequel M,Berrou C.Iterative correction of intersymbol interference:Turbo equalization[J].European Transactions on Telecommunications,1995,6(5):507-511.
[9] Tüchler M,Singer A C.Turbo equalization:an overview[J].IEEE Transactions on Information Theory,2011,57(2):920-952.
[10] Christophe L,Raphael L B.Adaptive MMSE Turbo equalization with high-order modulations and spatial diversity applied to underwater acoustic communications[C]//Proceedings of the 11th European Wireless Conference.Vienna,Austria:IEEE,2011:1 -6.
[11] Robertson P,Villebrun E,Hoeher P.A comparison of optimal and sub-optimal MAP decoding algorithms operating in the log domain[C]//Proceedings of 1995 International Conference on Communication.Seattle,WA IEEE,1995:1009 -1013.
[12] Brink S.Convergence behavior of iteratively decoded parallel concatenated codes[J].IEEE Transactions on Communications,2001,49(10):1727 -1737.
[13] Tüchler M,Singer A C,Koetter R.Minimum mean square error equalization using a priori information[J].IEEE Transactions on Signal Processing,2002,50(3):673-683.
[14] 肖扬.Turbo与LDPC编解码及其应用[M].北京:人民邮电出版社,2010:26-27.XIAO Yang.Principleof Turbo and LDPC codes and their applications[M].Beijing:People's Posts and Telecom Press,2010:26-27.(in Chinese)

