油料保障资源调拨运输优化模式分析和模型实现
文/刘奇韬 何 奇 穆 鑫
一、研究背景
油料调拨运输优化是实施油料保障的重要环节,是油料主管部门根据油源、储备油料品种与数质量情况、部队消耗、油库位置能储油能力,对油料的有序流动作出的计划安排,它是军队油料供应的源头,是完成各项油料保障任务的重要手段,主要包括炼油厂或国家储备油库调往军队后方油料、后方油库之间调运、后方油库给部队调运等三种方式。本文主要研究的是油料调拨运输的第三种方式。
各种复杂的油料调拨运输问题主要是由若干单个油料需求点与单个油料供应点(简称“单对单”)、多个油料需求点与单个油料供应点(简称“多对单”)和多个油料需求点与多个油料供应点(简称“多对多”)组成,也就是说根据保障关系可将油料调拨运输问题划分为一个个“单对单”、“多对单”或“多对多”问题,或者由这三种模式综合而成。这样就将复杂的油料调拨运输优化问题分解为相对简单的三种模式,既便于研究也容易系统实现。
模型研究借助了网络优化、军事运筹、模糊数学和地理信息等技术方法,在实现战时油料调拨运输过程中不同含权方式多目标优化问题的基础上,针对战时油料调拨过程中“单对单”、“多对单”和“多对多”等模式分别建模并对模型进行应用实现。
二、“单对单”运输优化模式
“单对单”模式,是最简单的保障模式,只有一个油料保障点、一个油料需求点,是属于典型的两个固定点之间寻求最优路径的问题。假设油料保障点是A、油料需求点是B,A到B经过n个节点的路网,则其目标函数为:
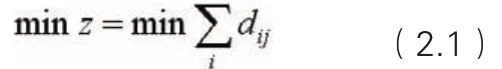
在“单对单”模式下,运用不同含权方式油料输送路径优化模型,选择不同优化方式,实现油料调拨运输优化。关于两个固定点之间寻求最优路径的问题和不同含权方式油料输送路径优化模型,这里不进行详细的阐述。
这里主要给出实现的思路和流程:首先确定部队油料需求点,包括所需油料的品种、数量,需求点空间位置的确定根据实际需要通常可以提供两种方式:一是根据经纬度方式确定,这种方式适合后勤保障命令、指示中提供了经纬度信息;二是在地图上直接确定,这种方式操作简便,便于指挥员综合考虑交通道路、水源情况、隐蔽性、与作战对象之间距离等因素,灵活确定需求点的空间位置。其次,是否有特殊要求,即是否有不能通行的道路,或者必须通行的道路,一般前者相对普遍。最后运用多目标优化模型的有效路径优化算法实现油料调拨运输优化。其流程如图1所示。
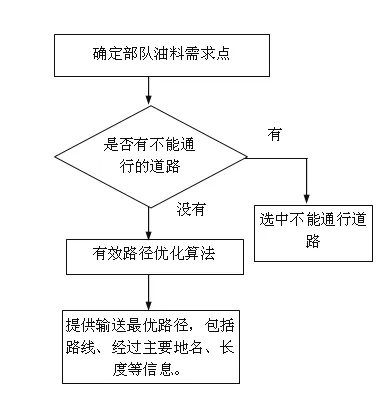
图1 “单对单”保障流程
三、“多对单”运输优化模式
“多对单”模式,是一种较复杂的油料调拨运输优化模式。在油料需求点确定的情况下,需要对当前保障对象的保障能力、空间分布及道路交通等信息进行分析,根据选定的油料输送优化方式,从众多保障对象中选出最优的保障对象及保障品种、数量,明确其输送路线。
1.模型建立
假设在某一作战方向上,有1个油料需求点a,对油料的需求量分别为(k=1,2,…,s),s 为油品数量;选定的m个油料库站承担其油料供给任务,分别是(j=1,2,…,m),其储量分别为(j=1,2,…,m,k=1,2,…,s)。

然后对距离关系矩阵D进行排序,根据就近保障原则,依次找到最小距离的油料库站进行保障,使得总距离最短。

2.模型实现
“多对单”模式油料调拨运输优化是根据道路交通条件进行的,模型实现有两种主要方法。
(1)第一种方法是以部队油料需求点所在地为运算起点。运用路径优化算法,从该点出发沿着与其相连的道路(公路、铁路、管线)进行发散型搜索,对在搜索过程中遇到的保障实体及其保障能力进行判断,如果保障实体无保障能力或者不属于保障范围,则程序继续搜索,如果保障实体有能力进行保障则将实体的相关信息(地理位置、连接道路、油料储备、保障油料数量)记录下来,如果保障任务的需求量已得到满足则停止搜索,否则继续搜索。其流程如图2所示。
在监督机制建设中要重点强化企业的成本监督和相关管理工作,要以成本作为监督的目标,理顺企业生产、管理的经济关系,从成本控制的角度构建起有针对性、可执行的监督平台和监督制度,真正将监督工作的重点放在对企业各项成本的控制工作上,提升企业成本管理、运营管理的效率,打造企业在生产、管理和经营上的经济、组织与成本优势。
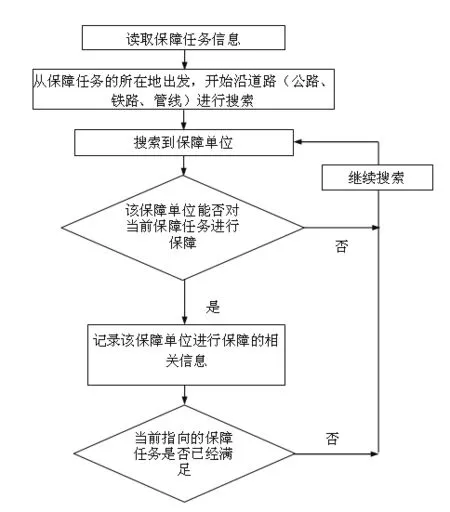
图2 “多对单”保障流程
(2)第二种方法是以油料保障点所在地为运算起点。运用路径优化算法,获取所有参与保障的油料库站与油料需求点之间的距离关系矩阵,然后按照就近保障原则,优先选择距离最短的油料库站,计算其油料品种、数量,如果不能满足保障任务,则继续选择距离次短的油料库站,直至满足油料需求为止。
3.应用举例
在某次抢险救灾中,某工程团作为先头部队提前到达指定地域。假设第二批部队到达之前,该工程团需要汽油、柴油分别为2000立方米、400立方米;选定的4个油料库站承担其油料供给任务,其储量分别为(j=1,2,,3,4,k=1,2),如表3.1所示。由路径优化算法求出各个需求点与各个供应点之间最短距离关系矩阵D,单位百公里。运用调拨运输优化模型确定油料调拨运输优化结果。
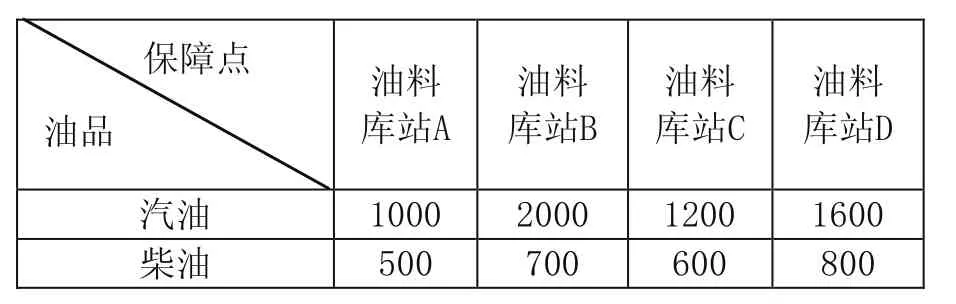
表3.1 各个油料库站的储油品种数量(立方米)
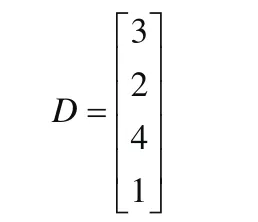
根据距离关系矩阵,优先确定油料库站D,根据其汽油、柴油容量和油料需求量,仍然缺乏400立方米汽油,再次确定油料库站B,则满足油料需求。因此油料调拨的结果是:油料库站D保障汽油、柴油分别是1600立方米、400立方米,油料库站B保障汽油400立方米。运输优化就是按照相关油料库站(D、B)与油料需求点之间的最短路径进行输送。
四、“多对多”运输优化模式
“多对多”模式,是最复杂的保障模式,也是战时最经常遇到的保障问题,是该部分研究的重点和难点。要解决多个油料保障点与多个油料保障对象的之间优化保障问题,须如下步骤。
1.模型建立
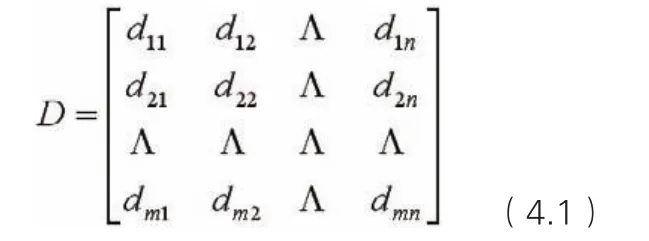
然后对距离关系矩阵D进行总排序,根据就近保障原则,依次找到最小距离的油料库站进行保障,使得总距离最短。
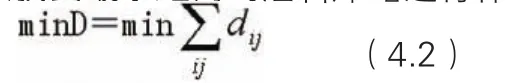
2.模型实现
“多对多”模式的模型基于GIS实现主要有两种情况,三种方法。
(1)油料需求任务有优先级区分。在此情况下,依据油料需求点的优先级别依次进行调拨运输优化,也就是说将“多对多”优化模式转换成“多对单”优化模式,然后按照“多对单”模式的模型进行优化。
(2)油料需求任务没有优先级区分。此种情况下有两种方法:一是先用A*算法或Dijkstra算法,求出所有需求点与保障点之间的距离关系矩阵,然后比较所有矩阵元素,按照就近保障的原则,也就是从小到大的顺序依次确定保障点,直至需求任务完成;二是把油料需求点所在地作为运算起点,从该点出发沿着与其相连的道路进行搜索,对在搜索过程中遇到的油料库站进行判断,如果不属于保障范围或无保障能力则继续搜索,否则将保障实体的保障油品数量记录下来,如果保障任务已得到满足则停止搜索,否则继续搜索。其流程如图3所示。
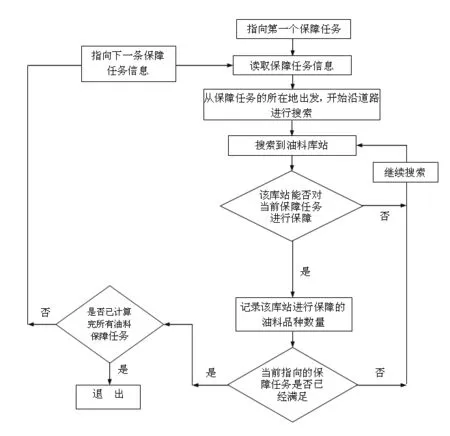
图3 “多对多”保障流程
探索完成后汇总,明确各油料需求点由哪些油料库站进行保障,各单位保障的油料品种及数量以及这些油料库站在进行保障时途经的最佳路径。
对于部分油料需求任务有优先级区分,部分没有的情况,或者优先级别出现相同的情况,则对所有油料需求任务进行优先级别排序,能够区别则按第一种情况处理,如果没有优先级别或者优先级别相同,则按照第二种情况处理。
最终,通过决策优化,明确各油料保障任务由哪些保障单位进行。
3.应用举例
在联合作战中,假设有四个单位承担作战任务,各单位对油料的需求量分别为(i=1,2,3,4,k=1,2),k代表汽油、柴油两种油品,如表4.1所示;选定的8个油料库站承担其油料供给任务,其储量分别为(j=1,2,…,8,k=1,2),如表4.2所示。由路径优化算法求出各个需求点与各个供应点之间最短距离关系矩阵D,单位百公里。运用调拨运输优化模型确定油料调拨运输结果。

假设油料需求点没有优先级别,则按照第二种方法求解,其求解步骤如下:
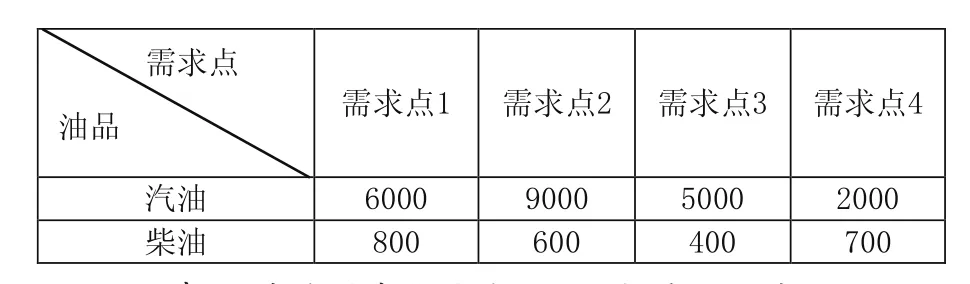
表4.1 各个需求点需要的油品数量(立方米)
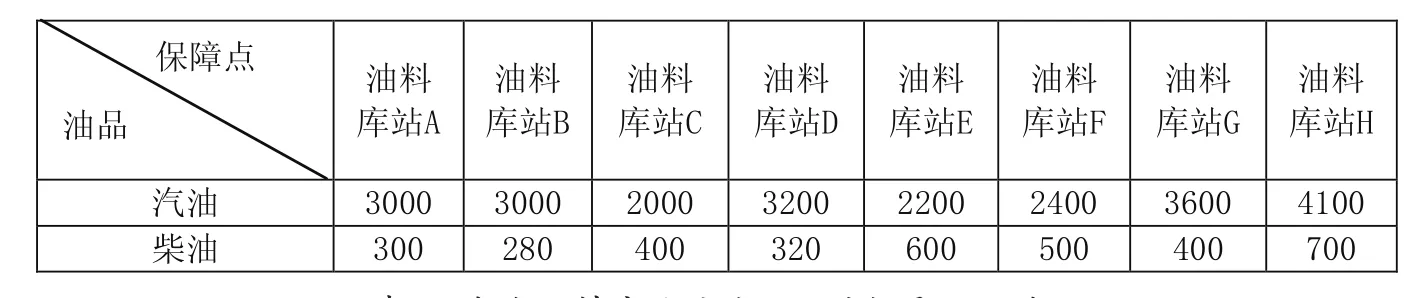
表4.2 各个油料库站的储油品种数量(立方米)

表4.3 汽油调拨优化结果

表4.4 柴油调拨优化结果
(1)从各需求点与各保障点之间的距离关系矩阵,找出最小距离为1.1,对应需求点1与油料库站D,油料库站D全部保障后,需求点1还差汽油、柴油分别是2800立方米、320立方米。把油料库站D相关的距离设为∞,即距离关系矩阵变为:

继续进行第二步。
(2)最小距离为1.2,对应需求点2与油料库站A,油料库站A全部保障后,需求点2还差汽油、柴油分别是6000立方米、300立方米。把油料库站A相关的距离设为∞,继续进行探索。
(3)最小距离为1.3,对应需求点4与油料库站B,油料库站B全部保障后,需求点4还差柴油420立方米,但是油料库站B的汽油还余1000立方米。此时既不能把与需求点4相关的路径设置为∞,也不能把与油料库站B相关的路径设置为∞,只能把它们之间的路径d42设置为∞。此时距离关系矩阵变为:

省略中间计算过程,直接给出调拨优化结果:各油料库站对应各需求点保障的汽油、柴油分别见表4.3、表4.4。
运输优化则由相关油料库站按照其保障的油料需求点之间的最短路进行。
五、小结
本文重点解决了不同模式的油料调拨运输优化问题,将多目标优化问题归结到单目标的路径优化问题,并结合例子分析其应用;将复杂油料调拨运输优化问题分解为若干“单对单”、“多对单”和“多对多”问题,然后针对“单对单”、“多对单”和“多对多”三种模式下的油料调拨运输优化,建立模型并基于地理信息分析了模型实现,最后给出应用举例进行验证,为油料调拨运输优化系统开发实现提供了相应模型及实现思路。

