基于模型诊断技术的神经网络实现方法

马纪明 万 蔚 王法岩

(北京航空航天大学中法工程师学院，北京100191)(北京航空航天大学 可靠性与系统工程学院，北京100191)

随着系统的复杂程度不断提高，其可能出现的故障随之增加，用于维护系统的成本也随之升高.故障诊断是保证系统能够安全可靠地完成预定目标的重要手段［1］.故障诊断流程主要有以下4个步骤［2］:故障检测、故障类型判断、故障识别、故障恢复，其中故障检测以及故障识别是最为关键的两步.

故障检测是故障诊断的基础，其目的在于检测系统是否有故障发生，从而控制是否启动故障诊断的后续步骤.常用的故障检测技术是将系统模型的预测值与实际系统的观测值相比较，检测是否一致，从而判断系统是否发生故障［3-4］.进一步又可分为基于状态估计方法、等价空间法和参数估计方法等［5］，三者各有特点，但参数估计方法因其具有充分利用已有信息挖掘系统更多的信息的特点［6-7］，得到了广泛的应用.

故障识别是故障诊断的核心，其目的在于对已检测出的系统故障进行识别，为后续的故障恢复提供依据.故障识别技术主要有专家系统［8］、故障树［9］等，然而专家系统和故障树均有一些局限性:专家系统故障识别结果的准确程度依赖于知识库中专家经验的丰富程度和知识水平的高低，且当规则较多时，推理过程中存在匹配冲突、组合爆炸等问题;故障树是建立在元件联系和故障模式分析的基础上，不能识别未知的故障以及识别结果依赖于故障树信息的正确性和完整性.

人工神经网络因其具有丰富的网络结构［10］，从而可以灵活地用于不同的系统.文献［11］运用神经网络对非线性系统故障状态下的参数进行估计，并根据估计参数进行故障诊断;BP(Back Propagation)神经网络具有模拟实际系统输入输出间的连续映射关系的能力［10］，可用于系统的参数估计;ART2(Adaptive Resonance Theory)神经网络具有非监督学习的特点，可以对未知模式进行自学习和记忆，从而成为已知模式［12］，因此可应用于缺乏先验故障信息的系统.论文采用BP神经网络对系统参数进行估计，结合系统模型进行故障检测，以及采用ART2神经网络进行数据聚类，基于聚类结果进行系统故障识别.

具体结构如下:第1部分介绍诊断系统的工作流程;第2部分设计采用神经网络的故障诊断系统的运行原理;第3部分以永磁直流电机为案例验证所提出的诊断系统的实用性;第4部分对所研究的内容进行总结，并指出有待进一步研究的内容.

1 诊断系统工作流程

研究设计采用人工神经网络实现的基于模型的故障诊断方法主要有故障检测和故障识别两个阶段.图1所示是利用神经网络实现的故障诊断系统的流程.

图1 故障诊断系统流程

在故障检测阶段，运用BP神经网络对诊断系统的输入进行处理分析，推理出更加丰富的系统信息.由神经网络推理产生的信息有两种类型:

1)系统理想状态的参数估计值:依据实际系统理想状态下的数学模型，构建一个BP神经网络，以此作为被测系统的参数估计模型，通过该估计模型对实际系统运行状态下的参数进行估计;

2)系统正常状态的预期输出:利用神经网络的函数拟合能力，模拟系统在正常状态下的输入输出响应，进而获得系统的预期输出.

在神经网络完成对输入信息的加工分析后，将系统参数估计值与参数正常值，以及系统运行的预测值与实际系统的观测值分别进行比较，以检测系统是否发生故障，进而实现故障检测.

在故障识别阶段，根据比较所得的差值以及系统运行数据进行特征提取，特征提取结果用于ART2神经网络的数据聚类，从而得到故障分类及识别结果.

2 诊断过程中神经网络的运行原理

2.1 故障检测/参数估计

根据参数估计的要求，设计了如图2所示改进的BP神经网络用于参数估计.

图2 BP神经网络逻辑结构图

其中，w1～wl，t1～tk分别为 l维和 k维神经元权值列向量，第i个神经元的权值列向量wi=［wi1，wi2，…，win］T，其中 wij为神经元的第 j个神经元的权值，同样地定义 ti=［ti1，ti2，…，til］T;由输入层输入列向量 X= ［x0，x1，…，xn］T;gi为隐含层第一层中第i个神经元的激活函数，gi的参数zi=XTwi;将这一层神经元的输出结果记为向量G=［g0(z0)，g1(z1)，…，gl(zl)］;fi为下一层神经元中第i个神经元的激活函数，fi的参数pi=GtTi.在输入层、隐含层以及输出层分别增加节点x0，g0，f0，其中x0恒为1，输入层除x0外的节点不作为g0节点的输入，同样隐含层除g0外的节点不作为f0节点的输入，从而可以拟合方程中出现的常量.以隐含层中第二层神经元为例，其输出如下式:

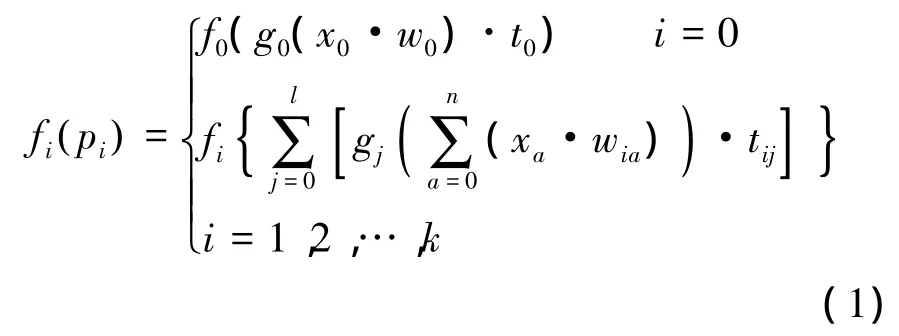
fi(pi)为输入X的一个复合函数，同时考虑到BP神经网络中的隐含层能够包含多层神经元，由此可以理解BP神经网络具有描述复杂函数模型的能力.

利用BP神经网络描述系统物理特性所对应的数学模型，具体步骤为:

1)假设系统数学模型F(t，Uin，P)可分解为

2)搭建一个BP神经网络，其隐含层的神经元层数与系统数学模型函数被分解后的子函数层次数目一致，例如式(2)所示，原函数被分解为两个层次，故而建立一个由两层神经元搭建起的前馈神经网络，数学模型中的系数，将由神经网络中权值表示.

设计了基于梯度下降法的神经网络学习算法，训练BP网络，使其权值自动调整到能使网络输出最接近于预想输出的状态.在训练过程中，神经网络的输入是实际系统的输入量，网络的预想输出为实际系统对应变量的值.训练完成后神经网络的权值即对应系统中参数的估计值.

2.2 故障识别/数据聚类

ART2神经网络的总体结构以自适应谐振理论为基础，并对其原型［10］结构进行了改进，将自底向下的长时记忆LTM_U与反应层合在一起，并添加筛选神经元和定向神经元以便能更好地运用于故障识别，诊断系统中实际构建的ART2神经网络结构如图3所示.

ART2神经网络由感受层、反应层、筛选层、定向神经元、LTM_D、输出层6部分构成.由反应层连接权值组成的列向量 W=［w1，w2，…，wn］T(w1～wn为同一个反应层神经元的对应权值)和LTM_D结构中的输出向量代表了网络中自下而上与自上而下记忆模式的中心参考向量.设定一个夹角阈值作为归类准则，并计算新模式与网络中习得模式的参考向量的夹角，从而判断新模式与该习得模式是否是同一类.夹角阈值由警戒参数描述，警戒参数保存于定向神经元中.

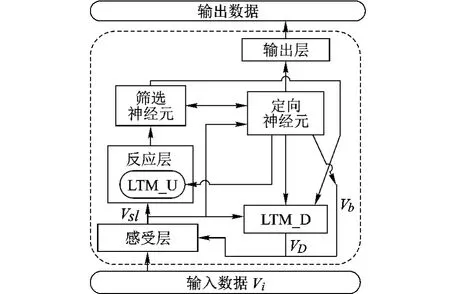
图3 ART2神经网络结构

3 案例验证

根据论文提出的故障诊断系统流程，本节以永磁直流电机为案例对该流程进行验证.永磁直流电机内部结构复杂，通常无法直接通过传感器监测其内部工作状态，而BP神经网络可以通过有限的外部监测信号实现对系统内部参数进行估计，以及ART2神经网络可以利用估计出来的参数进行故障识别.

3.1 仿真模型设计

在实际的永磁直流电机中植入各种故障状态较难实现，为了便于案例研究的开展，在Matlab/Simulink中搭建直流电机的性能仿真模型作为被测系统.

表1为仿真模型的参数，表2为直流电机的常见状态.

在电机模型中电路构成模块将依据绕组位置，确定绕组与电刷组成的临时电路形态，并且结合磁力/感应电动势模块反馈的感应电动势计算出电机中各个绕组内部的电流状态;磁力/感应电动势模块根据各个绕组的位置以及绕组电流，确定绕组产生的电磁力矩，另外通过绕组和磁极的位置以及绕组转动速度计算电机运转过程中产生的感应电动势.

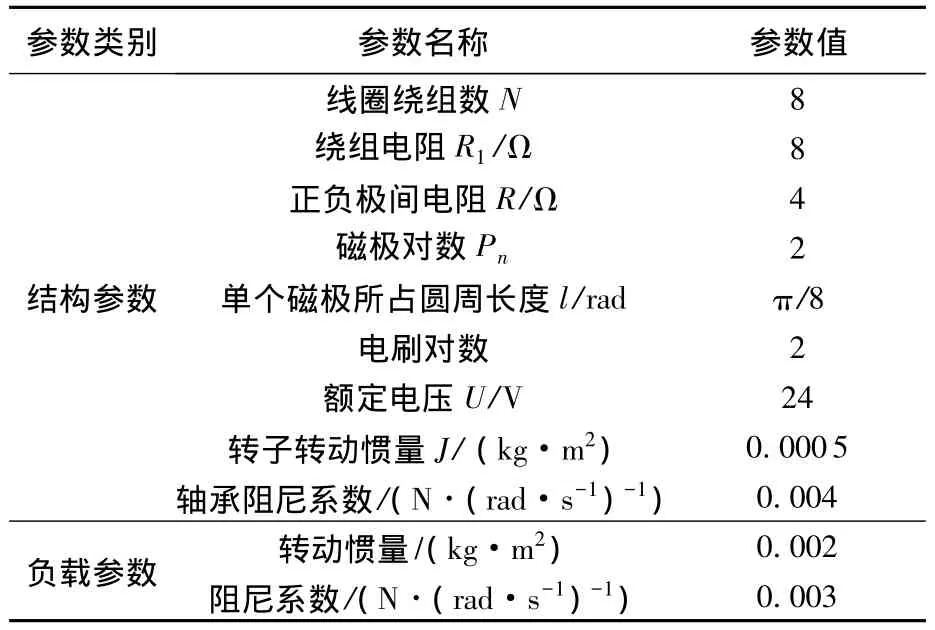
表1 直流电机仿真模型参数值

表2 直流电机常见状态

电机的仿真模型结构［13］如图4所示.

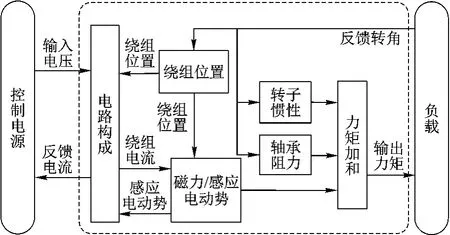
图4 电机模型结构图

在模型中电路构成模块承担模拟电刷开路、绕组开路、电刷安装位置与中性面没有准确对齐这三种故障模式的仿真实现;轴承故障由轴承模块实现.

3.2 诊断系统设计

在对实际电机进行监控的过程中，通常可以采集到的参数有:电机输入压U，电枢电流I，转速n，转矩T，由此确定故障诊断系统的输入数据为［U，I，n，T］.

由于直流电机系统整体结构复杂，难以用确切的解析模型进行描述，因此在诊断系统中引入电机正常状态参考模型和参数估计模型辅助构建故障诊断系统，模型与被测系统之间的关系如图5所示.

设计BP神经网络充当正常状态参考模型，其作用是根据实际系统输入电压U以及负载转速n推出电机在正常状态下的电枢电流Ii以及输出转矩Ti.

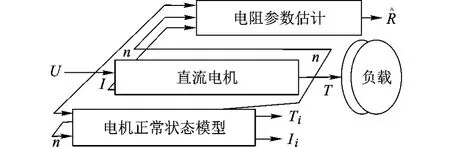
图5 模型与被测系统结构关系

参数估计模型是通过电机的输入电压U、电流I以及转速n，结合式(3)［14］设计的另一个BP神经网络(如图6所示)，其结构为2输入(U，I)1输出(n)，用于估计电机的电阻值

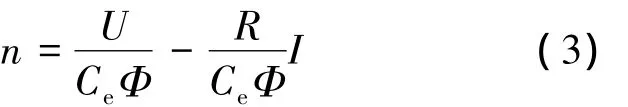
其中，Ce为电动势常数;Φ为励磁磁通.

图6 用于电阻值R估计的BP神经网络结构

利用BP神经网络的训练过程实现电机参数估计，在训练过程中将电机系统输入电压和电枢电流通过网络输入层输入神经网络，电机系统转速为输出.当神经网络完成训练后，隐含层神经元(采用线性激活函数)的权值(A，B)将会收敛于电机的实际参数1/CeΦ与R/CeΦ.输入端传入数值1，即可在参数估计端口获得 1/CeΦ与R/CeΦ的估计值，进而得到电阻的估计值R^.

借助于正常状态参考模型和参数估计模型，获得3个新的参数:电阻R^、正常状态下的电枢电流Ii以及输出转矩Ti.

最后采用ART2神经网络对实际监测数据和推理所得数据进行数据聚类，聚类结果对应于被测电机的工作状态.经过学习的ART2神经网络，再次接收监测数据和推理结果后，将依据已有的分类知识对输入内容进行自动分类，实现对系统工作状态的辨识和故障识别.

设计故障识别系统，首先应确定所需使用的数据特征.这里定义了5个用于故障识别分类的变量:

1)α为恒定参考值:α=1;

2)x1衡量正常电流Ii与实际电流I是否一致:x1=Fcha(Ii/I);

3)x2衡量正常转矩Ti与实际转矩T是否一致:x2=Fcha(Ti/T);

4)x3衡量正常电阻值R与估计电阻值R^是否一致:x3=Fcha(R/);

5)x4表示正常电阻值与估计电阻值比值:x4=R/.

根据电机诊断的需求，将ART2神经网络设计成如图7所示5输入6输出的结构，ART2神经网络的输入为特征提取过程的结果，即α，x1，x2，x3，x4.另外在ART2网络的输出端配置一个简单感知器用于将ART2网络的输出直接翻译为故障分类编号.

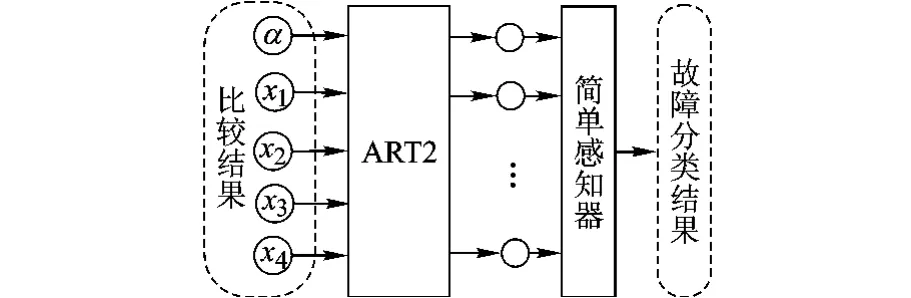
图7 用于故障识别的神经网络结构

3.3 结果分析

实际运行被测系统与相关推理模型，获取电机运行状态的先验信息.图8～图10展示了电机在部分状态下运行过程中电枢电流和输出转速.

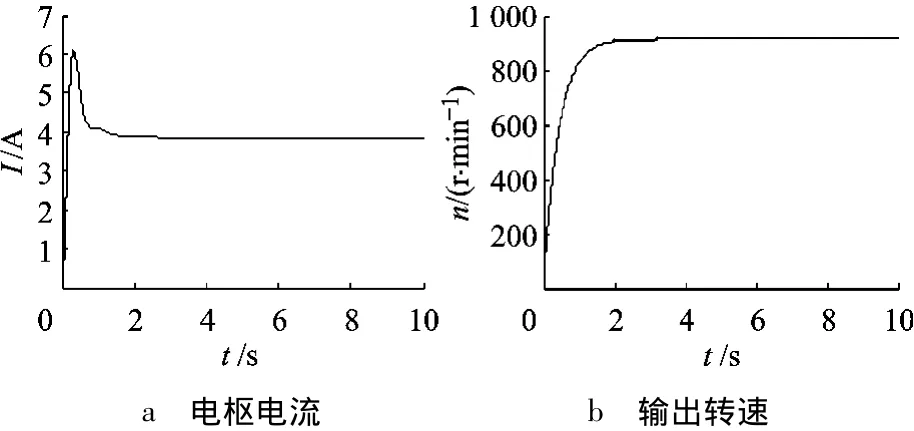
图8 电机处于正常状态

图9 电机在第3秒时轴承故障

用于ART2神经网络训练的电机在F0～F3 4种状态时稳态运行及推理结果如表3所示.

将结果作为经验信息，转为ART2的格式后输入网络进行数据聚类，警戒参数设为0.91，反应层有6个神经元.神经网络将4组数据分为4个类别，分类编号与输入顺序相同.神经网络的输入与输出信息如表4所示.

图10 电机在第3秒时绕组开路

表3 用于训练ART2的各状态稳态运行结果

表4 训练ART2的输入输出

在通过先验信息完成分类网络训练后，改变电机的工作状态，即改变电机负载.工作负载转动惯量减少为 0.001 kg·m2，阻尼系数变为0.0025 N/(rad/s)，并仿真 F0～F4状态.所得稳态均值以及推理结果如表5所示.

表5 实际运行稳态均值以及推理结果

表6 ART2输入参数与分类结果

表6中F0～F3状态数据输入ART2网络后，神经网络除了能够准确地从已有记忆中筛选出与输入数据相一致的类别，还能将F4状态区别于前4种状态，并将判别结果输出.实现了对已知和未知状态进行识别.

建立电机的正常状态参考模型以及正负极间电阻值的参数估计模型，将电机运行过程中的实际检测数据输入模型，并得到模型推理结果，即正常状态电枢电流、输出转矩和估计得到的电阻值.将实际测量值与推理值进行对比，产生用于训练ART2神经网络的先验学习样本，经过训练的ART2网络具有识别系统状态的能力.最后改变电机的工作状态，对训练后故障诊断系统进行验证，结果表明:诊断系统可以对电机发生的故障进行有效的检测和识别.

4 结论与展望

针对MBFD(Model-Based Fault Diagnosis)流程中故障检测和故障识别两个关键步骤，设计实现了采用BP/ART2神经网络的诊断系统.对永磁直流电机进行故障诊断，证明采用BP神经网络进行参数估计可以准确地估计电机不同状态下的参数，进而为故障检测提供有效依据;采用ART2神经网络进行数据聚类不仅可以识别电机的已知故障，而且可以识别出电机的未知故障，对先验信息较少的系统进行故障识别很有效果，具有一定的工程实用性.

有待研究的内容:①神经网络是通过连接权值存储信息，所以该方法对诊断结果的可解释性一般.在后续的研究中可以结合解释性较强的专家系统，设计融合二者优点的MBFD系统;②利用BP神经网络进行参数估计需要足够的系统数据(故障数据)进行训练.在后续的研究中可以寻求更完善的建模手段，以便能真实地对系统各种故障进行仿真以获得故障数据.

References)

［1］Rolf Isermann.Fault-diagnosis applications:model-based condition monitoring:actuators，drives，machinery，plants，sensors，and fault-tolerant system［M］.Germany:Springer，2010

［2］夏虹，刘永阔，谢春丽，等.设备故障诊断技术［M］.哈尔滨:哈尔滨工业大学出版社，2010:4－5 Xia Hong，Liu Yongkuo，Xie Chunli，et al.The fault diagnosis technology of equipment［M］.Harbin:Harbin Institute of Technology Press，2010:4－5(in Chinese)

［3］Venkatasubramanian V，Rengaswamy R，Yin K，et al.A review of process fault detection and diagnosis partI:quantitative modelbased methods［J］.Computers and Chemical Engineering，2003，27(3):293－311

［4］Venkatasubramanian V，Rengaswamy R，Kavuri S N.A review of process fault detection and diagnosis part II:qualitative models and search strategies［J］.Computers and Chemical Engineering，2003，27(3):313－326

［5］Zhang Huaguang，Wang Zhanshan，Liu Derong.Global asymptotic stability of recurrent neural networks with multiple time-varying delays［J］.IEEE Transactions on Neural Networks，2008，19(5):855－873

［6］周东华，胡艳艳.动态系统的故障诊断技术［J］.自动化学报，2009，35(6):748－758 Zhou Donghua，Hu Yanyan.Fault diagnosis technology of dynamic system［J］.AAS，2009，35(6):748－758(in Chinese)

［7］顾颖.一类非线性时滞系统的参数故障检测和估计［J］.大连交通大学学报，2010，31(2):95－97 Gu Ying.Parameter fault detection and estimation of a class of nonlinear systems with time-delay［J］.Journal of Dalian University，2010，31(2):95－97(in Chinese)

［8］Wu J D，Wang Y H，Bai M R.Development of an expert system for fault diagnosis in scooter engine platform using fuzzy-logic inference［J］.Expert Systems with Applications:An International Journal，2007，33(4):1063－1075

［9］Zhang Xu，Zhao Dongmei，Qiu Chen，et al.The power grid fault diagnosis based on the abnormal changes of the grid structure and the dynamic fault tree［J］.Applied Mechanics and Materials，2011，48:1282－1285

［10］阮晓钢.神经计算科学——在细胞的水平上模拟脑功能［M］.北京:国防工业出版社，2006:119－120，301 Ruan Xiaogang.Neural computing science-modeling brain function at the cellular level［M］.Beijing:Nation Defense Industry Press，2006:119－120，301(in Chinese)

［11］王占山，张恩林，张化光，等.基于Hopfield神经网络的非线性系统故障估计方法［J］.南京航空航天大学学报，2011，43(s):19－22 Wang Zhanshan，Zhang Enlin，Zhang Huaguang，et al.Fault estimation approach for a class of nonlinear systems based on Hopfield neural network［J］.Journal of Nanjing University of Aeronautics＆ Astronautics，2011，43(s):19－22(in Chinese)［12］Carpenter G A，Grossberg S.The ART of adaptive pattern recognition by a self-organizing neural network［J］.Computer，1988，21(3):77－88

［13］邱国平，邱明.永磁直流电机实用设计及应用技术［M］.北京:机械工业出版社，2009:13－54 Qiu Guoping，Qiu Ming.Practical design and applied technology of permanent magnet DC motor［M］.Beijing:China Machine Press，2009:13－54(in Chinese)

［14］廖晓钟，刘向东.自动控制系统［M］.北京:北京理工大学出版社，2005:9 Liao Xiaozhong，Liu Xiangdong.Automatic control system［M］.Beijing:Beijing Institute of Technology Press，2005:9(in Chinese)