基于缩放实验的Whipple结构撞击特性

张晓天 贾光辉

(北京航空航天大学 宇航学院，北京100191)

随着太空探索的进一步深入，空间碎片防护也成为一个关注热点.目前能进行可靠追踪和躲避的多为低地球轨道上大于10 cm的碎片，为了抵御更多无法观测的小碎片撞击，必须为大型航天器设计防护结构.这就需要对空间碎片撞击防护结构的过程——超高速碰撞过程进行研究.

目前的超高速碰撞分析技术包括地面碰撞实验和数值仿真两大类.地面碰撞实验准确度高，但是设备复杂，成本高;数值仿真易于实施，成本低，是开展大量研究的有效途径.空间碎片撞击航天器的平均相对速度大于7 km/s［1］，而目前的实验设备只能对7 km/s以下的球形弹丸撞击进行可靠有效的实验.7 km/s以上撞击特性只能通过外推的方式获得.另一方面，数值仿真技术虽然能够对大于7 km/s的撞击问题进行仿真，但由于缺少有效的实验验证，分析结果并不十分令人信服.

近些年提出了一种缩放实验方法来研究超高速撞击，用高密度低熔点材料(镉，Cd)的较低速撞击实验，来预测低密度高熔点材料(铝，Al)的较高速撞击实验.这个技术最早由文献［2］提出，用于研究半无限靶的成坑问题;随后文献［3］研究了Whipple防护结构后板的临界穿透厚度问题;文献［4-9］发展了缩放实验方法，研究了碎片云形态问题、弹道极限问题、斜撞击问题以及多层防护板问题，并提出了与著名的Christiansen弹道极限曲线［10］不同的7 km/s以上的弹道极限规律.

以上研究都是基于实验，超高速碰撞实验的复杂性与成本导致了获得的实验数据数目很有限，只能用个别工况来验证缩放实验理论，并且缺乏适用性分析;实验分析手段只能获得撞击结果数据，而缺乏关键过程参数，难以进行撞击机理的细致研究;对与Christiansen弹道极限曲线不吻合的结果，也难以展开深入讨论.

实验研究成果为数值仿真提供了验证依据，本文以上述文献中的实验结果为基础，开展了数值仿真研究.首先通过与实验结果对比验证了数值仿真的有效性和正确性，然后对缩放实验方法的适用性进行了讨论，对可能影响缩放相似性成立的材料失效机理进行了分析.最后研究了7 km/s以上Whipple防护结构的弹道极限规律，针对Christiansen与Schmidt结论的矛盾给出了一种解释.

1 缩放实验方法与仿真验证

1.1 缩放实验方法

在7 km/s以下的超高速碰撞问题中，弹丸和防护结构的材料多处于破碎并包含熔化的状态.然而在更高速的碰撞问题中，弹丸侵彻防护屏的物理过程发生了变化，材料的熔化和气化成为主导.因此直接将7 km/s以下的分析结果外推以得到7 km/s以上结果的方法并不可靠［4］.

缩放实验方法假设Whipple防护结构的后板失效主要受前板后碎片云比冲量的影响，碎片云比冲量则是一系列结构参数以及材料参数的函数，可由下式［4］表示:

其中，I是比冲量;δ是材料密度;h是材料的单位质量熔化能;H是单位质量汽化能;U为撞击速度;Y是强度极限.在此基础上，用结构参数完全相同的“替代材料”替换原有的弹丸和前板的铝材料(后板保持不变).通过选择替代材料，能够构造和铝材料相同的碎片云比冲量，进而就能够对后板形成一致的损伤能力.替代材料的选择要求满足下列缩放相似性条件［4］:

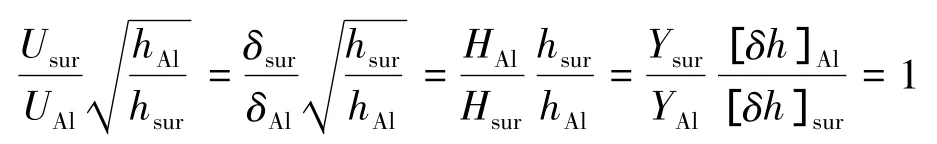
其中下标Al表示铝材料参数;sur表示替代材料参数.Cd材料具有相对于Al更大的密度，更小的融化点和汽化点，其独有的特性恰好满足缩放相似性条件;并且撞击速度为U的Cd实验就能够构造与撞击速度为3.1U的Al实验等价的碎片云.这变相的拓展了现有加速设备所能研究的撞击速度极限.

1.2 7 km/s的数值仿真验证

文献［4］中对7.2 km/s的 AL实验和 Cd实验(缩放等效速度)进行了对比验证(参见图1和表1)，这是Piekutowski所使用的加速设备的极限.本文首先使用数值仿真，对这两个实验进行对比验证.数值仿真采用LS-dyna软件，2D轴对称模型，仿真算法为SPH方法.材料模型为适用于超高速碰撞问题的Steinberg强度模型和Gruneisen 状态方程［11-12］.

图1 7.2 km/s实验结果与仿真结果对比

从图1中可以发现:①Al实验和其缩放等效Cd实验的碎片云非常相似，实验表明缩放实验方法是有效的.②无论是Al撞击还是Cd撞击，碎片云仿真结果和实验的一致性很好.③Al弹丸的破碎程度要略大于Cd弹丸，这一点仿真结果和实验也是一致的.

表1 7.2 km/s实验与仿真对比

表1给出了实验穿孔直径和仿真穿孔直径的定量对比.以上结果表明，仿真分析是正确有效的.另外，Al撞击和Cd撞击的碎片云几何形态以及穿孔直径都非常相近.注意到由于Al弹丸直径略大于Cd弹丸(没有严格满足结构参数相同)，所以实验中Al穿孔直径也略大于Cd的穿孔直径.仿真验证了缩放实验方法的有效性.

1.3 7 km/s以上的数值仿真验证

由于在7 km/s以上的情况，对于Al撞击已经超出了现有加速设备的极限，因此无法给出缩放相似性的实验验证.Schmidt和Piekutowski只给出了Cd的缩放等效实验结果.本文建立了1405和1419缩放等效速度下Al撞击仿真模型，实验参数如表2所示.并且以Cd撞击实验结果对Al数值仿真进行了验证(见图2).

表2 7 km/s以上实验参数

图2所示，Al仿真与Cd实验碎片云几何形态一致性很好，表明缩放实验方法在7 km/s以上的有效性，也表明数值仿真应用于7 km/s以上的有效性.

图2 7 km/s以上实验结果与仿真结果对比

2 数值仿真分析

在数值仿真技术得到验证的基础上，应用仿真对缩放实验方法的适用性进行了讨论.

2.1 弹丸形状适用性分析

实验中使用的是球形弹丸，本文保持防护屏尺寸不变，改变弹丸形状(见图3)，包括:圆柱、圆锥和复杂形状弹丸.总体来说依然保持了较好的相似性.但是当使用非球形弹丸时，Al撞击与Cd撞击的差异有所增大.另外，Cd弹丸的破碎程度同样要大于Al弹丸.这种差异在非球形弹丸问题中带来的影响更加明显.

图3 不同弹丸形状仿真结果对比

2.2 撞击速度适用性分析

为了检验缩放仿真方法对速度的适用性，对3～18 km/s的速度范围进行了Al-Al撞击和Cd-Cd撞击的数值仿真对比.由图4可见，对＞3 km/s，Al-Al撞击问题与Cd-Cd撞击问题产生的碎片云有较好的一致性，而3 km/s时的碎片云差异较大.这与文献［4］中指出的:＞4 km/s时两者一致性较好，也是相同的.另外，不同速度的仿真对比表明，随着撞击速度增加，弹丸的破碎程度增大.进而使得碎片云轮廓由“鸡蛋”形转变为近似球形.

2.3 Whipple防护结构

缩放实验法对于前板后碎片云具有很好的适用性.本节进一步讨论碎片云对Whipple防护结构后板的影响.图5给出了1415a和1422两个实验所对应的Whipple防护结构的仿真结果.

表3给出了穿孔直径的仿真结果和误差.仿真结果与实验结果较一致.后板仿真计算穿孔误差大于前板穿孔误差.

图4 不同撞击速度仿真结果对比

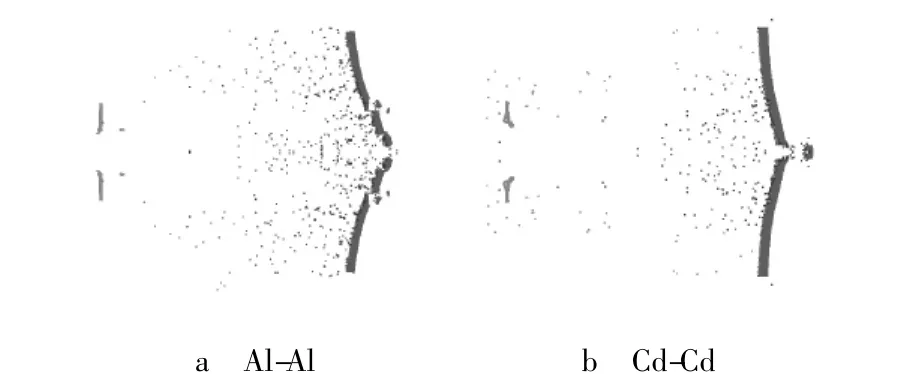
图5 Whipple防护结构的仿真结果

但是，由Al-Al撞击和Cd-Cd撞击的后板结果对比来看，无论是实验还是仿真，两者存在较大的差异.图5中可见Al-Al撞击中后板出现了断裂，而Cd-Cd撞击只表现为中心穿孔，两者的中心穿孔的直径相近.

表3 Whipple防护结构结果对比

由于Al与Cd的相似性条件是近似满足的，这个误差造成了实验结果的差异.另外，数值仿真计算原理与真实物理作用过程之间也存在一定误差，这个误差造成了仿真与实的差异.把超高速碰撞过程看作一个系统，如果这个系统是连续的，那么微小的系统误差会引发微小的结果差异.比如前面的单层板穿孔问题，Cd与Al的结果误差以及仿真和实验的误差都比较小，说明单板穿孔直径对输入条件是连续依赖的.然而如果这个系统是不连续的，那么微小的系统误差就可能引发很大的结果差异.而此处的Whipple结构后板穿孔问题就表现出了不连续性.下面进一步深入讨论.

2.4 连续性讨论

表4给出了文献［4］中实验的几组数据，未列出的结构参数与表1、表2中相同.对比1415a和1416a可发现两个实验条件很相近，但是后板穿孔结果相差很大.对比1439*和1440*也会发现这个问题.这表明工况参数的细微差异造成了后板穿孔直径的很大差异.本文进行了多种影响因素的分析，通过单因素连续变化调整，研究后板的失效模式变化.下面以“后板失效应力”这个因素为例进行说明.

表4 实验数据结果

考虑到材料参数的误差，失效应力的真实值可能与文献调研值有一定的误差.本文通过比例缩放的方法讨论了后失效应力值的误差对失效模式的影响，如图6.“强度因子”后板材料失效应力比例缩放系数，其中参考值为文献中调研得到的失效应力取值.当强度因子在0.1～0.2时，后板失效模式表现为多处穿孔;强度因子在0.3～0.4时，后板表现为中心穿孔外加局部崩裂;强度因子在0.5～0.8时，后板表现为中心穿孔;强度因子在0.9左右时，后板表现为中心穿孔外加多处鼓包;强度因子在1.0左右时，后板表现为多处断裂.在失效模式发生变化的情况下，对于穿孔直径的测量值就会发生跳变，甚至难以定义.

图6 典型的后板失效形式

综合实验和仿真结果，后板穿孔直径乃至失效模式受到工况参数和材料参数的显著影响，甚至是不连续的影响.这个结论为缩放实验方法带来了一个深层的疑点:由于文献［4］构造Al-Al撞击与Cd-Cd撞击的等价性条件是近似成立的，所以在式(1)中的f函数不连续时，等价性条件的微小误差造成的两者撞击结果的差异可能是很大的.

2.5 弹道极限分析

使用数值仿真方法对8～18 km/s的速度段进行了弹道极限分析.结果如图7所示.Christiansen的曲线是由7 km/s以下的数据外推得到的，在8～18 km/s范围内是单调递减的.Schmidt的曲线是通过Cd缩放实验得到的，先递减而后递增，与 Christiansen的曲线差别很大.NumSimu1和NumSimu2为本文仿真得到的弹道极限曲线.圆点为仿真数据点，其中实心圆点表示穿透，空心圆点表示未穿透.从图7可见，仿真结果得到了两条弹道极限曲线，由大约9 km/s处开始发生分叉，且两条曲线分别和Christiansen的曲线以及Schmidt的曲线一致.

图7 弹道极限曲线对比

图8给出了18 km/s撞击速度下，不同弹丸直径对应的后板失效情况.从图中可发现，随着弹丸直径从2.4 mm增大至10.8 mm，后板经历了“未穿透-穿透-未穿透-穿透”的变化.相应的产生了多个弹道极限点.

图8 不同弹丸直径对应的后板失效

由2.4节的讨论可知，后板失效形式不连续依赖于工况参数.本文当弹丸比较小时，形成中心微小穿孔.随着弹丸增大，碎片云直径增大，从而后板着靶面积增大，反而降低了中心压强，不再产生穿孔.随着弹丸进一步增大，后板出现大范围鼓包，当增大到一定程度后，整个鼓包发生破裂，形成大穿孔.按照这样的模式推理，弹道极限曲线可能不止两条，随着弹丸进一步增大可能会出现更多的分叉.比如18km/s时，9.6 ～10.8mm 之间显然存在一个极限点.

3 结论

本文以缩放实验方法为基础，结合数值仿真技术，讨论了7 km/s以上的超高速碰撞问题.获得了如下结论:

1)建立了数值仿真模型，获得了与实验一致的仿真结果，表明了仿真技术的正确有效性.

2)数值仿真表明，满足缩放相似性的Al-Al和Cd-Cd撞击碎片云存在很强的相似性.

3)数值仿真表明缩放仿真实验方法对弹丸形状适应性较好;对于3～4 km/s以上的速度范围适应性较好;对于Whipple的后板存在一定误差，且后板的失效形式对工况参数的依赖是不连续的.

4)受后板失效模式不连续性影响，Whipple结构7 km/s以上的弹道极限曲线出现分叉现象.

References)

［1］WrightD.Spacedebris［J］.PhysicsToday，2007，60(10):35-40

［2］Morrison R H.Simulation of meteoroid velocity impact by use of dense projectiles［R］.NASA D-5734，1970

［3］Hopkins A K，Lee T W，Swift H F.Material phase transformation effects upon the performance of spaced bumper systems［J］.Journal of Spacecraft and Rockets，1972，9(5):342-345

［4］Schmidt R M，Housen K R，Piekutowski A J.Cadmium simulation of orbital-debris shield performance to scaled velocities of 18km/s［J］.Journal of Spacecraft and Rockets，1994，31(5):866-877

［5］Schmidt R M，Housen K R，Bjorkman M O，et al.Advanced allmetal orbital debris shield performance at 7 to 17 km/s［J］.International Journal of Impact Engineering，1995，17(4-6):719-730

［6］Housen K R，Schmidt R M.Cadmium simulations of high-speed impacts—the hole story［R］.AIAA 1996-4365，1996

［7］Poormon K L，Piekutowski A J.Comparisons of cadmium and aluminum debris clouds［J］.International Journal of Impact Engineering，1995，17(4-6):639-648

［8］Cour-Palais B G，Littlefield D L，Piekutowski A J.Using dense，low melting point projectiles to simulate hypervelocity impacts on typical spacecraft shields［J］.International Journal of Impact Engineering，1995，17(1-3):241-251

［9］Piekutowski A J，Poormon K L，Christiansen E L，et al.Performance of whipple shields at impact velocities above 9 km/s［J］.International Journal of Impact Engineering， 2011， 38(6):495-503

［10］Reimerdes H G，Nölke D，Schäfer F.Modified Cour-palais/christiansen damage equations for double-wall structures［J］.International Journal of Impact Engineering，2006，33(1-12):645-654

［11］徐小刚.航天器防护结构超高速撞击弹道极限方程综合建模方法研究［D］.北京:北京航空航天大学宇航学院，2009 Xu Xiaogang.Ballistic limit equations integrated method of spacecraft shields under space debris hypervelocity impact［D］.Beijing:School of Astronautics，Beihang University，2009(in Chinese)

［12］胡振东.碎片对航天器蜂窝夹层板结构超高速碰撞研究［D］.北京:北京航空航天大学宇航学院，2007 Hu Zhendong.Numerical investigations of space debris hypervelocity impact on spacecraft honeycomb panel structure［D］.Beijing:School of Astronautics，Beijing University of Aeronautics and Astronautics，2007(in Chinese)