利用CFD技术计算飞行器动导数
叶 川 马东立
(北京航空航天大学 航空科学与工程学院,北京100191)
动导数是飞行器动稳定性分析必需的数据.随着计算流体力学(CFD,Computational Fluid Dynamics)技术的发展,特别是非定常流场数值模拟研究的进步,已经可以利用CFD方法进行飞行器动导数计算.在国内,文献[1]计算了超声速尖锥、钝锥、弹道外形和飞船返回舱的俯仰静、动导数.文献[2]数值模拟了NACA0012翼型跨声速俯仰振荡过程中法向力系数和俯仰力矩系数随迎角的变化及弹道外形和有翼导弹在不同初始迎角下的俯仰静导数和动导数.国外也有不少学者利用 CFD 工具进行了动导数的计算[3-4].这些方法一般通过非定常流场计算模拟飞行器强迫俯仰振荡得到俯仰方向的动导数.模拟飞行器强迫俯仰振荡得到的动导数计算结果是俯仰力矩系数对迎角变化率和俯仰角速度的动导数之和,但飞行器动稳定性分析需要获得二者单独的数值.
本文利用滑移网格进行非定常计算,模拟强迫俯仰振荡运动,得到俯仰力矩系数对迎角变化率和俯仰角速度的动导数之和.利用旋转参考坐标系进行定常计算,模拟飞行器定常拉升运动,计算俯仰力矩系数对俯仰角速度的动导数(俯仰阻尼导数),从而得到单独的俯仰力矩系数对迎角变化率和俯仰角速度的动导数.利用旋转参考坐标系模拟飞行器匀速滚转,计算滚转力矩系数对滚转角速度的动导数(滚转阻尼导数).计算结果与试验数据、文献数据以及其他方法获得的结果具有较好的一致性.
1 滑移网格
滑移网格的主要思想是将计算区域划分为滑移区域和静止区域.滑移区域内的网格随着离散的时间步变化沿旋转轴产生转动或发生平移,在不同的时刻重新生成网格;静止区域则保持不动.在滑移区域与其他区域的交界面处,利用搭接边界条件与其他区域对接,从而实现整体流场的计算.
与其他的动网格技术相比,滑移网格法的简便之处在于,其运动仅仅是滑移区域相对于静止区域的滑动,相对节省产生新网格所需的计算资源,并且运动过程中滑移区域的网格质量不发生变化,因此比较适合模拟复杂外形飞行器的转动或平动.
2 旋转参考坐标系
单一旋转参考坐标系多用于流体机械中流动的建模.在流体机械中,转子或者叶轮周期性的掠过求解域,相对惯性参考系来讲,流动是不稳定的,需要进行非定常流场求解.在不考虑静止部件的情况下,取随旋转部件一起运动的一个坐标系,则相对这个旋转参考系(非惯性系)来讲,流动就是稳定的,进行稳态流场计算即可,从而简化了问题的分析.
转动坐标系与绝对坐标系下的速度存在以下关系:

式中,vr为转动坐标系中的速度矢量,即相对速度;v为绝对坐标系中的速度矢量;ω为转动角速度;r为相对位置矢量.
以相对速度表示的质量守恒方程为
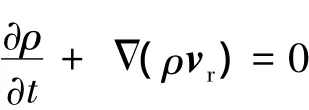
式中,ρ为流体密度;t为时间.
动量守恒方程为
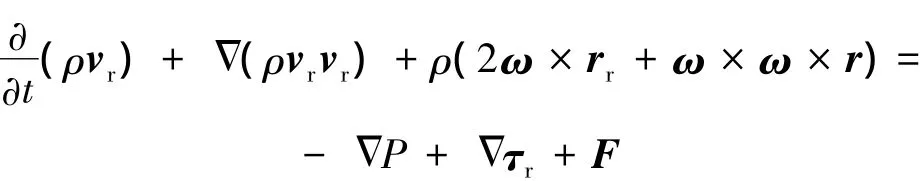
式中,P为压强;τr为相对粘性应力张量;F为彻体力.
能量守恒方程为
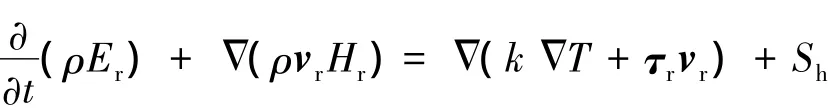
式中,Er为相对内能;Hr为相对总焓;K为流体传热系数;T为温度;Sh为粘性耗散项.
3 动导数计算方法
3.1 俯仰组合导数计算方法
飞行器俯仰组合动导数一般通过模拟飞行器低频小幅俯仰振荡过程进行计算.在定轴转动情况下,强迫运动方程为

式中,α为迎角;α0为初始迎角;αm为迎角振幅;ω为俯仰振荡频率.
根据线化气动力理论[5],俯仰力矩系数可表示为
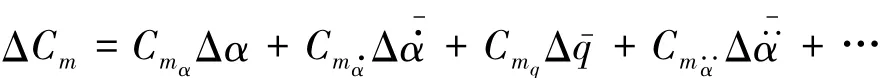
式中,Cm为俯仰力矩系数分别为归一化的迎角变化率和俯仰角速度;Cmα,Cmα·和 Cmq分别为俯仰力矩系数对迎角、迎角变化率和俯仰角速度的导数.对于常规飞行器来说,上式右边一般保留前3项即可.
显然,俯仰振荡过程中迎角变化率等于俯仰角速度,即
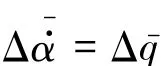
于是有:
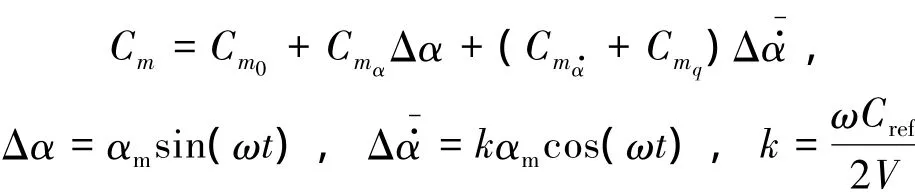
式中,Cm0为参考状态的俯仰力矩系数;k为减缩频率;Cref为参考长度;V为飞行速度.于是俯仰力矩系数可表示为以下形式:
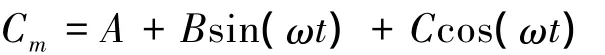
式中,A,B和C为待定系数.进行俯仰振荡非定常计算之后,可得到俯仰力矩系数随时间变化的曲线,通过最小二乘拟合可求出A,B和C这3个待定系数,从而得到静俯仰力矩系数和俯仰力矩导数.
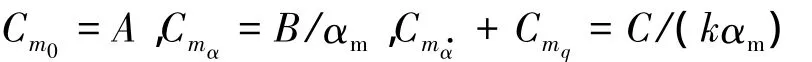
3.2 俯仰阻尼导数计算方法
通过模拟飞行器定常拉升运动计算俯仰阻尼导数.所谓定常拉升运动,是指飞行器在垂直平面内以恒定角速度进行圆周运动,如图1所示.在定常拉升过程中,飞行器的迎角保持不变,但俯仰角在不断变化,俯仰角速度不变.若选择一个固连在飞行器上,随飞行器一起作圆周运动的坐标系,对于这个坐标系来说,流动是稳态的,因而进行定常计算即可模拟运动过程.改变飞行器的俯仰角速度,进行若干次定常计算,得到俯仰力矩系数随俯仰角速度变化的曲线.若俯仰力矩系数随俯仰角速度线性变化,则可得到飞行器的俯仰阻尼导数.

图1 飞行器定常拉升
对于飞行器定常拉升运动,存在以下关系式:
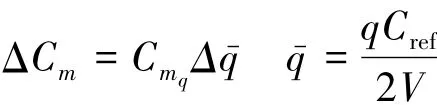
显然,飞行速度V与俯仰角速度成正比:

于是有:

即无因次俯仰角速度只与参考长度和旋转半径有关.
3.3 滚转动导数计算方法
通过模拟飞行器匀速滚转运动(图2)计算滚转阻尼导数.动稳定性研究一般选择对称定直平飞状态作为参考状态,在稳定坐标系中定义滚转角速度.在参考状态,飞行速度位于机体对称面内,则稳定坐标系与风轴系重合.在匀速滚转状态,飞行器以恒定角速度绕稳定坐标系纵轴旋转,对于固连在飞行器上,随飞行器一起滚转的坐标系来说,流动是稳定的.
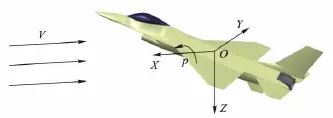
图2 在稳定坐标系中匀速滚转
若选择在通常使用的纵轴指向机头的机体坐标系中定义滚转角速度,则在迎角不为0的状态,机体坐标系纵轴与气流坐标系纵轴不重合,如图3所示.由于机体相对于来流的位置不断变化,无法利用旋转参考坐标系将非定常流动转换为定常流动.
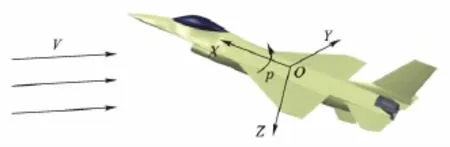
图3 在纵轴指向机头的机体坐标系中匀速滚转
对于匀速滚转运动,存在以下关系式:
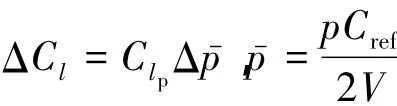
式中,Cl为滚转力矩系数;Clp为滚转阻尼导数;p为滚转角速度.
得到稳定坐标系下的动导数之后,可通过变换得到选定的机体坐标系下的动导数.任意选定的机体坐标系可由稳定坐标系绕Y轴旋转一个角度ε得到.以滚转阻尼导数为例,机体坐标系和稳定坐标系中的滚转阻尼导数存在以下关系[6]:
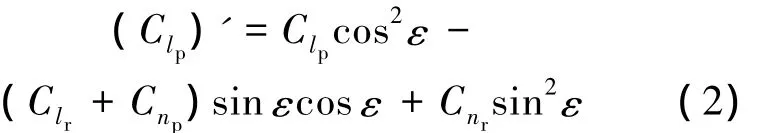
式中,(Clp)'为机体坐标系中的滚转阻尼导数;Cnr为偏航阻尼导数;Clr和Cnp为交叉导数.由上式可见,要将稳定坐标系下的滚转阻尼导数转换到机体坐标系中,还需要计算偏航阻尼导数和滚转力矩系数对偏航角速度的导数.
4 有翼导弹动导数计算
4.1 有翼导弹俯仰组合动导数计算
Basic Finner Missile有翼导弹模型是验证动导数计算方法经常使用的模型.此导弹长细比为10,头部为锥形,弹体为圆柱形,十字型尾翼.
网格划分采用非结构网格,计算外域为一圆柱体,滑移区域为外域内的一小圆柱体,表面网格如图4所示.计算条件与文献[7]试验条件相同.马赫数 M∞=1.96,雷诺数 Red=0.86×105,振幅θm=±1°,减缩频率 k=ωd/2V∞=0.008 6.其中,d为弹体直径,V∞为来流速度.

图4 有翼导弹表面网格
利用滑移网格模拟有翼导弹强迫俯仰振荡过程.空间离散方法为结合有限元方法的有限体积法,时间离散格式为二阶向后欧拉格式,采用剪切滑移(SST,Shear-Stress Transport)湍流模型.
计算了有翼导弹迎角为0°,5°和10°的俯仰组合动导数.如图5、图6所示,动导数、参考状态俯仰力矩系数计算结果与文献[3]结果接近,与试验结果[7]相比,在小迎角范围相差较大,在迎角较大时比较接近.计算结果与试验结果在小迎角下存在差异的原因可能是试验结果在小迎角状态受到支架的干扰[3].有翼导弹外形上下对称,理论上当迎角为0°时参考状态俯仰力矩系数应当为0,计算结果和文献结果都证明了这一点,但试验结果明显存在偏差.
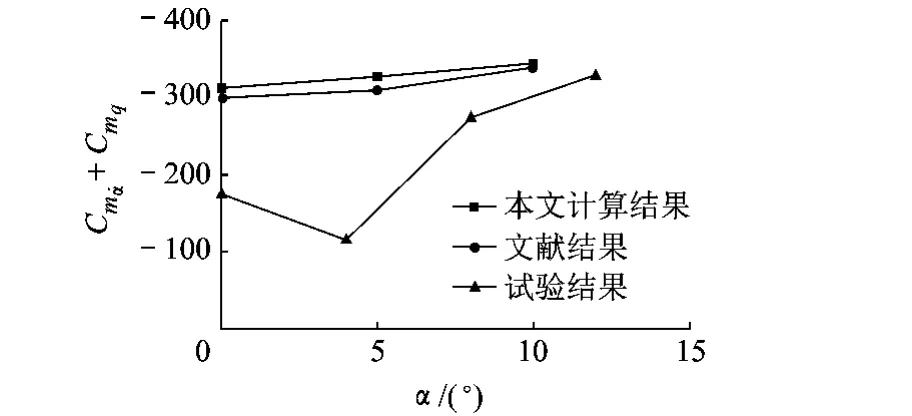
图5 俯仰组合动导数计算结果比较
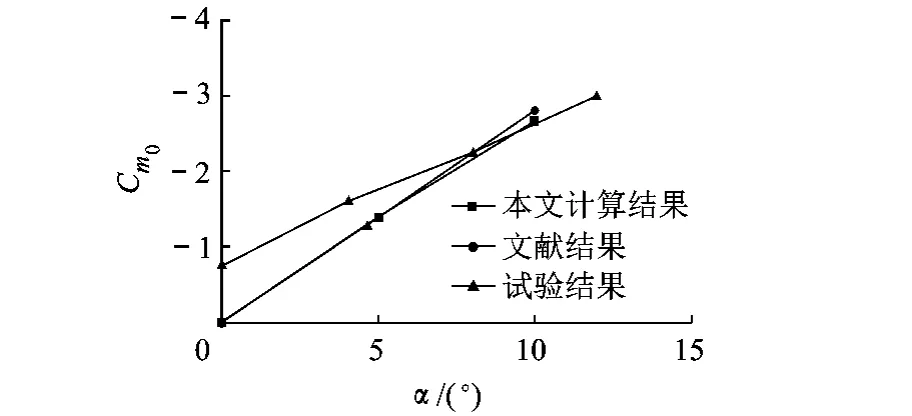
图6 参考状态俯仰力矩系数计算结果比较
4.2 有翼导弹俯仰阻尼导数计算
文献中并未提供有翼导弹模型的俯仰阻尼导数数据.利用旋转参考坐标系模拟有翼导弹模型的定常拉升运动,得到了此导弹模型的俯仰阻尼导数.计算使用的外形、来流参数与俯仰组合导数计算相同.
由式(1)可知,无因次俯仰角速度只与参考长度和旋转半径有关.为计算不同无因次俯仰角速度下的俯仰力矩系数,需要改变旋转半径.当旋转半径改变之后,为保持飞行器重心处速度不变,相应地需要改变计算区域的旋转速度.使用旋转参考坐标系方法时,需要设置计算区域的旋转轴和旋转速度.
在给定的迎角下计算3种状态,无因次俯仰角速度分别为0.0086,0.0172 和0.0258,得到了俯仰力矩系数随无因次俯仰角速度变化的曲线,如图7所示.由计算结果可见,俯仰力矩系数随无因次俯仰角速度增大而线性变化.对计算结果进行线性拟合得到有翼导弹在各个迎角下的俯仰阻尼导数.综合俯仰组合动导数计算结果,获得了分离的对迎角变化率和俯仰角速度的动导数.

图7 俯仰力矩系数随俯仰角速度变化
在计算的3个迎角下,有翼导弹的俯仰力矩系数对迎角变化率的导数与俯仰阻尼导数符号相同,俯仰力矩系数对迎角变化率的导数绝对值较小,不超过俯仰阻尼导数的14%,结果见表1.

表1 有翼导弹俯仰动导数计算结果
4.3 有翼导弹滚转阻尼导数计算
利用旋转参考坐标系方法模拟有翼导弹模型的匀速滚转运动,得到了滚转阻尼导数.计算模型尺寸,计算条件与文献[7]试验条件保持一致.马赫数 M∞=2.50,雷诺数 Red=1.86×105.
计算了迎角为0°和10°时不同滚转角速度下的滚转力矩系数,如图8所示.迎角为0°时,滚转力矩系数计算结果与试验结果符合得很好.对计算结果进行线性拟合,得到迎角为0°时的滚转阻尼导数Clp=-17.3,绝对值稍小于试验结果Clp=-18.
迎角为10°时,试验数据是纵轴指向弹头的机体坐标系中的滚转力矩系数,本文计算结果是稳定坐标系中滚转力矩系数.由式(2)可知,若迎角不大,则稳定坐标系和机体坐标系中的滚转阻尼导数相差不大.计算得到的稳定坐标系中滚转阻尼导数 Clp=-21.65,试验结果为 Clp=-20.
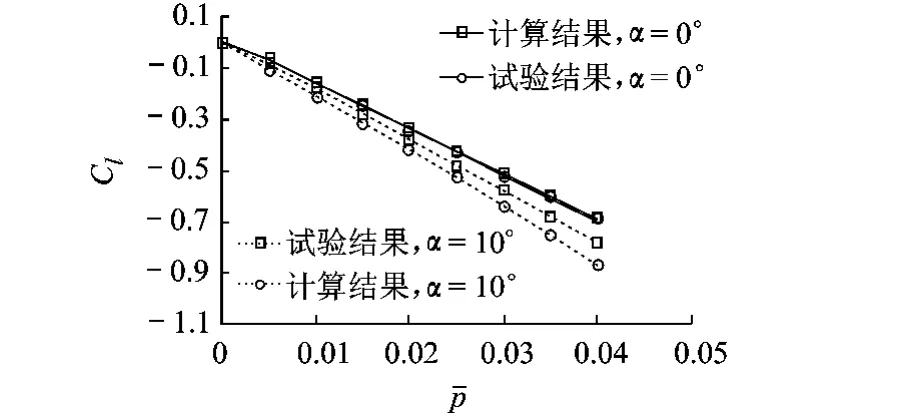
图8 0°,10°迎角滚转力矩系数计算结果
5 水上飞机动导数计算
为检验计算复杂外形飞行器动导数的效果,计算了一个自行设计的水上飞机在巡航状态下的纵向和横向动导数,并与面源法程序(AVL,Athena Vortex Lattice)和飞行器设计软件(AAA,Advanced Aircraft Analysis)的计算结果进行了比较.此水上飞机为鸭式布局,发动机舱位于机身上方,左右机翼下方各安装有一个浮筒,全机重心位于鸭翼和机翼之间,表面网格如图9所示.AVL是定常面源法程序,无法计算与时间有关的对迎角变化率的导数,AAA计算动导数使用经验公式,只计算翼面的影响.

图9 水上飞机表面网格
5.1 水上飞机俯仰组合动导数计算
水上飞机巡航状态纵向组合动导数计算方法、步骤与有翼导弹俯仰组合动导数计算相同.水上飞机俯仰组合动导数计算结果与AAA计算结果符号相同,但绝对值大于AAA计算结果,如表2所示.

表2 水上飞机俯仰组合动导数计算结果比较
5.2 水上飞机俯仰阻尼导数计算
俯仰阻尼导数计算结果位于AVL和AAA的计算结果之间,升力系数对俯仰角速度的导数大于AVL和AAA的计算结果(图10、表3).由于机翼距重心较远,机翼对全机俯仰阻尼导数的贡献较大,除机翼和鸭翼外,机身和浮筒也有一定贡献.AAA俯仰阻尼导数较小的原因可能是只考虑了翼面的影响.
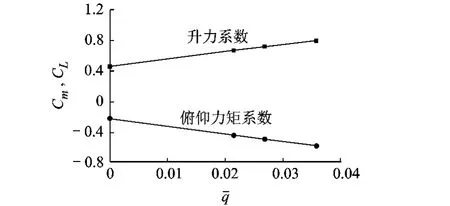
图10 俯仰力矩系数、升力系数随俯仰角速度变化

表3 水上飞机俯仰阻尼导数计算结果比较
综合俯仰组合动导数计算结果,得到了分离的俯仰动导数.与俯仰角速度导数相比,迎角变化率导数绝对值较小,计算结果和AAA计算结果在一点上是一致的.计算结果中除升力系数对迎角变化率导数之外,其他3个动导数与AAA计算结果符号相同.与AAA计算结果相比,计算得到的动导数绝对值较大,如表4所示.

表4 水上飞机俯仰动导数计算结果比较
5.3 水上飞机滚转阻尼导数计算
滚转阻尼导数计算结果(图11)绝对值稍大于AAA和AVL计算结果,偏航交感力矩导数计算结果绝对值位于AAA和AVL计算结果之间.本文计算结果和AAA计算结果中的机翼滚转阻尼导数接近,但AAA由于只考虑了翼面的影响,全机滚转阻尼绝对值较小.但AAA计算得到的机翼偏航交感导数绝对值明显大于本文计算结果,全机偏航交感导数较大,如表5所示.
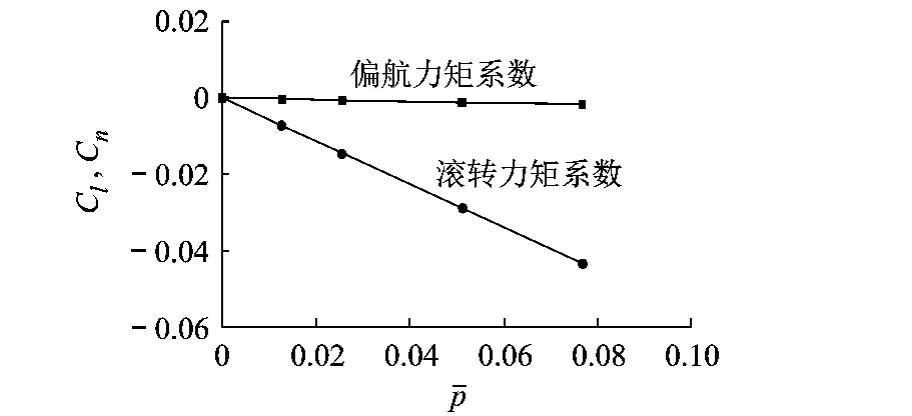
图11 滚转力矩系数、偏航力矩系数随滚转角速度变化

表5 水上飞机滚转动导数计算结果比较
6 结 束 语
两个算例并没有涉及航向动导数的计算.航向动导数的计算方法与纵向动导数计算方法类似,可先利用滑移网格方法计算航向组合动导数,然后利用旋转参考坐标系方法单独计算偏航阻尼导数.使用提出的动导数计算方法可得到飞行器稳定性分析所需的各个单独的动导数.网格划分使用非结构网格,且滑移网格在网格运动过程中网格质量不变,因此网格生成工作量较小,尤其是对水上飞机这类复杂外形.只需进行若干次稳态计算即可得到阻尼导数,计算量较小.提出的方法可用于复杂外形飞行器动导数的计算,具有较高的效率.
References)
[1]袁先旭,张涵信,谢昱飞.基于CFD方法的俯仰静、动导数数值计算[J].空气动力学学报,2005,23(4):458-463 Yuan Xianxu,Zhang Hanxin,Xie Yufei.The pitching static/dynamic derivatives computation based on CFD methods[J].Acta Aerodynamica Sinica,2005,23(4):458-463(in Chinese)
[2]范晶晶,阎超,李跃军.飞行器大迎角下俯仰静、动导数的数值计算[J].航空学报,2009,30(10):1846-1850 Fan Jingjing,Yan Chao,Li Yuejun.Computation of vehicle pitching static and dynamic derivatives at high angles of attack [J].Acta Aeronautica et Astronautica Sinica,2009,30(10):1846-1850(in Chinese)
[3]Murman S M.Reduced-frequency approach for calculating dynamic derivatives[J].AIAA Journal,2007,45(6):1161-1168
[4]Le Roy J F,Morgand S.SACCON CFD static and dynamic derivatives using ElSA[R].AIAA 2010-4562,2010
[5]方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:189-193 Fang Zhenping,Chen Wanchun,Zhang Shuguang.Aircraft flight dynamics[M].Beihang:Beijing University Press,2005:189-193(in Chinese)
[6]埃特肯B.大气飞行动力学[M].北京:科学出版社,1979:194-195 Etkin B.Dynamics of atmospheric flight[M].Beijing:Science Press,1979:194-195(in Chinese)
[7]Uselton B L,Jenke L M.Experimental missile pitch-and rolldamping characteristics at large angles of attack [J].Journal of Spacecraft,1977,14(4):241-247

