求解Burgers方程的一类指数积分方法

李雨，魏玉芬，朱焕

（黑龙江八一农垦大学理学院，大庆 163319）

Burgers 方程是描述非线性耗散现象的典型方程，很多学者在该方程的理论和数值求解方面进行了大量研究。求解Burgers 方程的主要方法是有限元方法和有限差分方法，这类方法一般采用差分方法在空间方向上进行离散得到常微分方程，然后在时间方向进行离散构造显式或隐式格式。而近年来发展起来的李群方法所采用的积分方法在稳定性方面更有优势，应用李群方法的思想可以构造一种基于积分格式的指数积分方法，数值算例表明这种显式方法在稳定性方面具有一定的优势。

1 基于李群方法的指数积分法

考虑形如

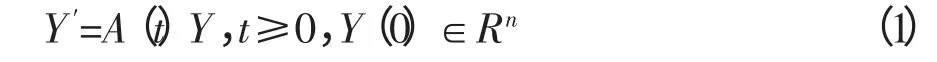
的线性常微分方程组，其中A：R→Rn×Rn，首先介绍关于指数映射[6]的一些概念。

定义1 指数映射exp：Rn→Rn定义为

其中，exp（O）=I，上述定义限定在矩阵李群的范围内。

定义2 称Ad 为伴随表示，若

其微分ad 定义为

其中，adA0B=A，adAn（B）=[A，[A，L[A，B]]]。

指数映射的微分记为

其中，dexp：Rn×Rn→Rn，与adA的关系为

当A 固定时dexpA（t）关于A′（t）是线性的，由的泰勒级数展开形式可得

由于dexpA是adA的解析函数，因此

又因为

其中，Bj为伯努利数，因此

基于上面的定义，关于方程（1）的解有如下引理，

引理1[1]设Θ（t）满足下列微分方程

则方程（1）的解为Y（t）=exp（Θ（t））Y0。

根据上述结论，求解微分方程（10）即可得到方程（1）的解，因此对方程（10）采用不同的数值方法求解，就得到了求解方程（1）的不同的数值方法。

对式（10）采用Picard 迭代，则

把重新排列各项并化简得

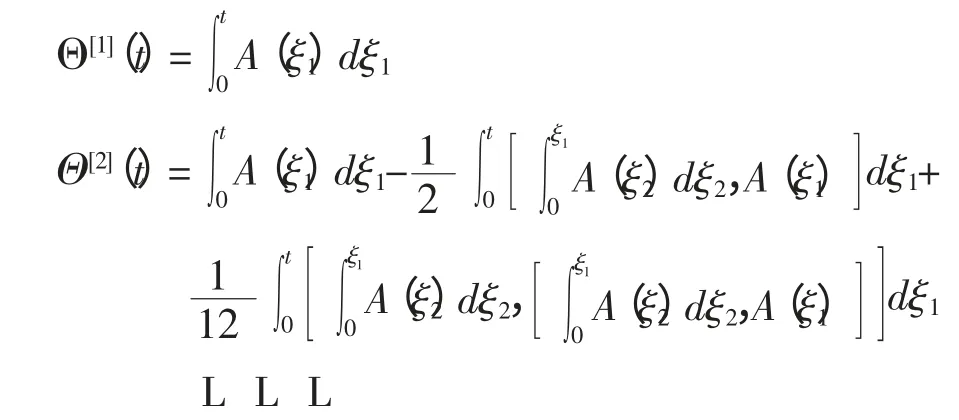
像这种把（10）的解Θ（t）写成矩阵A（t）的交换算子和积分的线性组合形式称为Magnus 展开[1-2]，根据Magnus 展开时的对称性把Magnus 展开写成

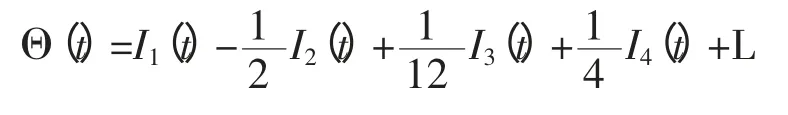
其中，

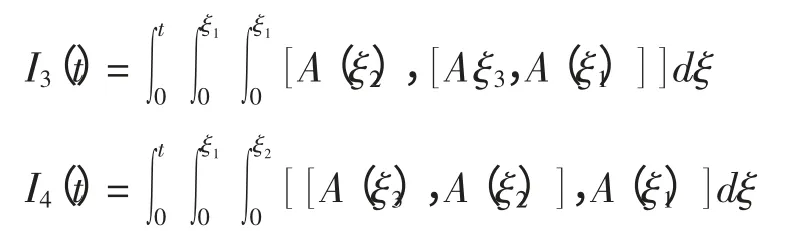
显然可以根据Magnus 展开的根数理论写出Ik的其他各项，参见文献[1，3-6]。

关于Magnus 展开的收敛性，已由Moan 证明了对于任意t∈（0，t*），考虑Euclidean 范数，Magnus 展开是收敛的。

下面对Magnus 展开进行数值应用，取步长h＞0，Magnus 展开中的项可以写成

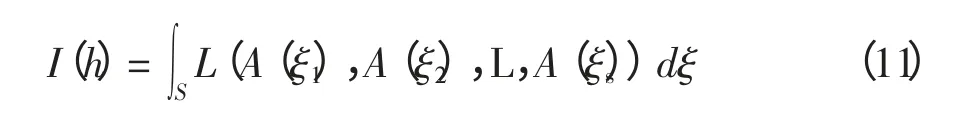
其中，S={ξ ∈RS：ξ1∈[0，h]，ξl∈[0，ξml]，l=2，3，L，s}，ml∈{1，2，K，l-1}，l=2，3，K，s。

根据Iserles 和Nørsett（1999）[7]的理论，对I（h）进行离散，取v 个积分节点c1，c2，L，cv∈[0，1]，记Ak=hA（ckh），k=1，2，L，v，则I（h）离散为

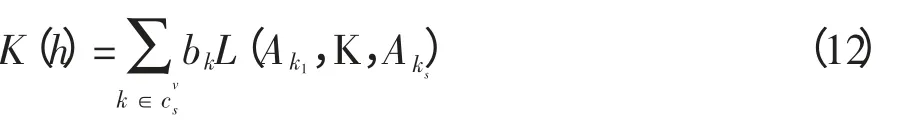
式（11）中的A（t）可以应用插值多项式在积分节点的值

代替，因此得到显式积分格式。

Iserles（1999）在文献[1]中证明了下面的引理：

引理2[1]由正交条件

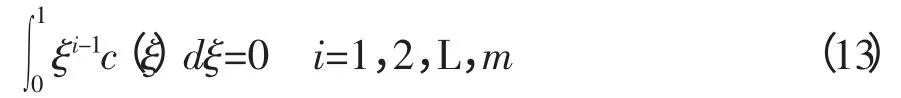
可知，对任意的S 和多项式函数L，数值积分（12）的阶为v+m；当c1，c2，L，cv是Lagendre 多项式Pv在区间[0，1]的根时，则数值积分（12）的阶可达2v，其中，m＞0 是使得上式成立的最大整数。

在非线性问题中，I（h）中的A 与Y 有关，即Ak=hA（ckh，Y（ckh）），由于Y 是未知函数，它在求积节点ckh 上的值是未知的。如何解决这个问题呢？设求积节点c1，c2，L，cv满足式（13）给出的正交条件，则相应的单变量值多项式的积分可达阶p=v+m，又因Ak都是h 的倍数，设Xk是Y（ckh）的不低于p-1 阶的估计值，显然可以用hA（ckh，Xk）来代替Ak。基于此，我们必须对Y（ckh）进行p-1 阶估计，配置方法来构造估计值Xk是一种简单而有效的方法，采用拉格朗日插值多项式

代替A（t，Y），此处Ak=hA（ckh，Xk）k=1，2，L v。

此时，对方程（10）仍然使用picard 迭代，可以得到一般的Magnus 展开[8-10]，在非线性情况下需要计算

基于上述理论，选取不同的积分节点即可构造各种显式和隐式方法。

定理1 方法

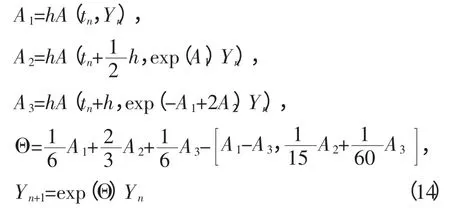
是求解非线性常微分方程

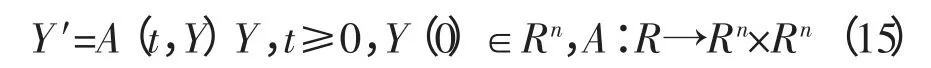
的三阶显式方法，称为指数积分法。

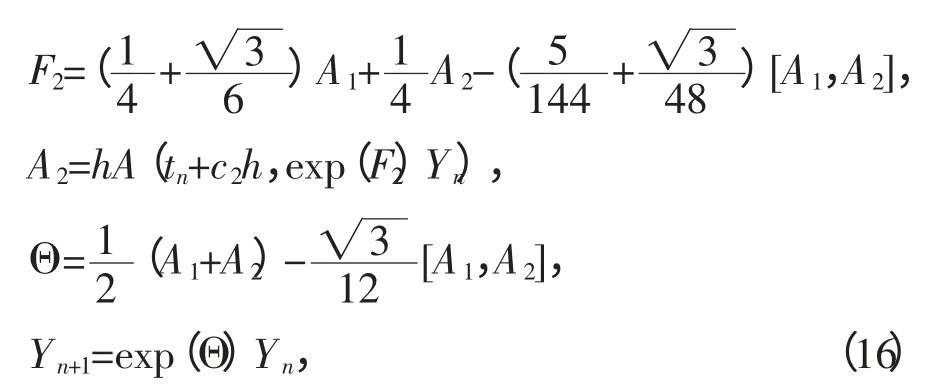
放松配置条件，即得指数积分方法（14），该方法的计算量很大，但在稳定性方面该方法有很强的优势。

2 应用指数积分法求解拟线性Burgers 方程

考虑形如

的拟线性Burgers 方程，取xi=iVx，u（xi，t）≈xi（t），i=1，2，L，N，用中心差分代替方程空间方向导数

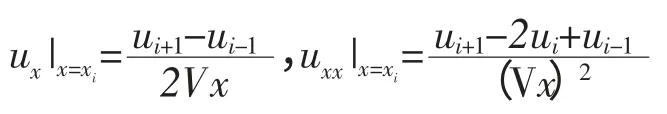
ui满足常微分方程

取U=（u0，u1，L，uN）T则方程（17）转化为非线性常微分方程组[10]

其中

此处cn=un+1-un-1，n=1，2，K N-1，I 为N+1 级单位阵。

于是Burgers 方程（17）转化为方程（16）的形式，可以使用指数积分法来求解。

3 数值算例

考虑Burgers 方程初值问题

其中

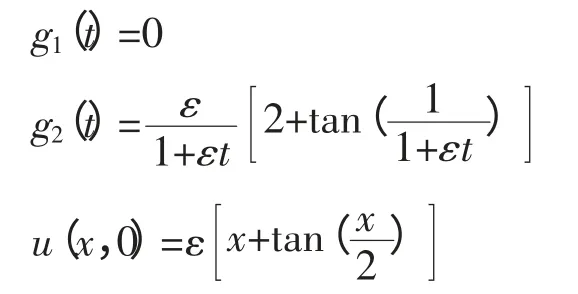
它的解析解为

下面将方程（18）进行离散，记U=（u0，u1，K，uN）T，则方程转化为

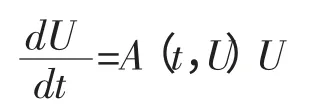
其中

A（t，U）为（N+1）×（N+1）矩 阵，cn=un+1-un-1，n=1，2，K N-1。

下面取ε=1，N=20（即△x=0.1），取xmin=0，xmax=2，分别应用指数积分法和三阶的Runge-Kutta 方法求解，从表1 可以看出两种方法在精确度相差不大的情况下，指数积分法对步长要求更低，换句话说，当对求解精度要求相同的情况下，指数积分法比其他方法稳定性更好。

表1 两种方法在求解Burgers 方程时的步长比较Fig.1 Two methods of Burgers equations

［1］A.Iserles ，S.P.Nørsett，H.Z.Munthe-Kaas，et al.Lie-Group Methods［J］.Acta.Numer，2000（9）：215-365.

［2］A.Iserles，A.Magnus Expansion for the （）Equation Y′=AY-YB［J］.J.Comput.Math，2001，19（1）：15-26.

［3］A.M.Bloch，A.Iserles.Commutators of Skew-Symmetric Matrices［J］.Intl J.Bif.Chaos，2005，15（3）：793-801.

［4］B.Owren.Order Conditions for Commutator-Free Lie Group Methods［J］.J.Phys.A-Math.Gen，2006，39（19）：5585-5599.

［5］A.Iserles.On Cayley -Transform Methods for The Discretization of Lie-Group Equations.Found［J］.Comput.Math，2001，1（2）：129.

［6］J.Q.Sun，Z.Q.Ma，M.Z.Qin.RK-MK Method of Solving Non-Damping Equtions and Ferromagent Chain Equations.Comput［J］.Appl.Math，2004，157：407-424.

［7］M.P.Calvo，A.Iserles，A.Zanna.Runge-Kutta Methods for Orthogonal and Isospectral Flows ［J］.Appl.Numer.Nov，1996，22（1-3）：153-163.

［8］F.Casas，A.Iserles.Explicit Magnus Expansions for Nonlinear Equations ［J］.J.Phys.A -Math.Gen，2006，39（19）：5445-5461.

［9］A.Iserles，S.P.Norsett.On the Solution of Linear Differential Equations in Lie Groups［J］.Philos.T.Roy.Soca，1999，357（1754）：983-1019.

［10］M.P.Calvo，A.Iserles，A.Zanna.Semi-Explicit Methods for Isospectral Flows.Adv［J］.Comput.Math，2001，14（1）：3-24.

［11］孙建强，秦孟兆.解Burgers 方程的一种显式稳定性方法［J］.计算数学，2007，29（1）：67-72.

［12］邓廷勇，孔令滨.一类四阶非线性微分方程边值问题正解的存在性［J］.黑龙江八一农垦大学学报，2010（6）：79-82.