高职院校经济应用数学精品课程建设的研究与实践

李良彬

（北京农业职业学院 基础部，北京 102442）

1 高职教育中经济应用数学教学的现状

1.1 高职教育中经济应用数学教学内容存在的问题

高职院校所用教材内容基本上是普通高等工科和经管类专业院校的压缩或翻版，忽略了高职教学的特点.目前我们所用经管类教材大体上有两类,一类是在微积分内容上基本是理工类教材的精简版,经管类所需要的线性代数和概率论仅介绍繁杂的概念和简单的计算,应用性方面一点而过,这对数学基础相对薄弱的学生来说缺乏实用性、趣味性,显得枯燥难懂;另一类则侧重于介绍数学文化,忽略了具体数学知识,更谈不上介绍数学思想,这类教材往往使学生体会不到数学的思维思想所在.

1.2 教学时数严重不足

2004年4月，教育部下发1号文件《教育部关于以就业为导向深化高等职业教育改革的若干意见》,提出要“积极进行高等职业教育两年制学制改革”,以此推动高职教育的课程体系改革和教学内容改革.两年制学制的推行在很大程度上压缩了各高职院校数学教学的课时，教学课时严重不足.由于教育部对数学教学课时没有明确要求，数学课的教学课时不断被减少，有些专业甚至停止开设数学课.目前我院经济应用数学只有60学时.一方面试图把大量的《经济应用数学》的基础知识介绍给学生,另一方面又受课时较少的限制而精简教学内容.

1.3 在教学方法和信息技术的应用方面还有很大的提升空间

由于教师大都习惯从理工科学生角度来讲授经济应用数学，从高职高专经管专业学生角度来看,经管类专业学生大部分是文科生,而高职高专院校的经管专业学生数学基础可能更加薄弱,这种教学模式只会使学生感觉数学抽象,若按照传统方式教学,教师就很难做到因材施教,无法使学生体会到经济应用数学在所学专业中的应用性,因此,学生必然感到经济应用数学难学又无用.开发Mathematica软件的数学家Wolfram在2010年指出，即使在美国，在校内的许多课程仍然在用手算，而在企业和社会上，他们所用的都是CAD软件，即机算.如果仍然只会手算，他们将被解雇，“School Math(学校数学)”不向“Real World Math(真实世界)”靠拢，会造成巨大的鸿沟，浪费大量的社会资源，影响国民经济的发展……，这段话明确的指出了，信息技术的飞速发展及计算机的广泛应用和当前经济应用数学教学模式中存在的弊端，也为改革当前经济应用数学，加强对学生数学应用能力的培养提供了新的思路.

2 经济应用数学精品课建设的主要内容

2.1 充分调研，把握定位

普通本科院校按照学科分类设置专业，而高职按照技术领域与职业岗位（群）的实际要求设置专业.作为我院农经专业群共享平台课，经济应用数学课程的建设应该是在职业能力基础上的系统开发，因此，弄清每一专业所面向的职业标准与能力要求，对经济应用数学与专业课的整合具有重大意义.开展对农经专业培养目标的职业能力的相关研究，使经济应用数学课程内容能针对不同的专业，面向职业岗位或职业岗位群，按照突出应用性、实践性的原则，结合专业基础课与专业课重组课程结构，让学生学习有用的数学，获得必需的知识.

2.2 转变思想，提高认识

课程教学思想的转变是精品课程建设的前提，高等职业教育是大众化的教育，更应贯彻以人为本的教育思想，提高学生的思想素质，培养学生自主创新意识及综合实践能力，加强学生用数学思想、概念、方法消化吸收专业概念和原理的能力，必须重视数学概念的教学；培养学生把实际问题转化为数学模型的能力，必须重视数学建模训练；培养学生求解数学模型的能力，必须结合计算机和数学软件进行教学.

2.3 循序渐进，整合教材

教材建设是高职高专经济应用数学课程建设的核心，教材是落实教育思想，实施教学目标的依据，是教学内容的细化，是教学过程的“脚本”，也是教学方法的载体.

根据各专业对数学知识的需求整合教学内容，将经济应用数学整合为四个模块——微积分模块+线性代数模块+数理统计模块+选修模块（选修课），每个模块又分成迎接挑战（专业相结合的案例）、循序渐进（为解决这个案例应具备的知识储备）、温故知新（已学知识的复习提升）、探索新知（最终解决问题的方法）、课外阅读（必要的理论知识补充）等部分.整个模块教学始终围绕实际问题（案例）如何解决这个中心展开，探究解决这个问题思路与方案，为了这个思路需要具备的什么知识，而所需要知识又是新问题，再接着探究解决这个新问题思路与方案，循环实施这个过程，一直到问题解决.

例如，导数概念的引入，我们选用熟悉的经济问题：某产品的总成本函数和总收入函数分别为

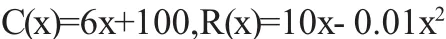
其中x为该产品的销售量

试问：（1）销售量增加一个单位时，总成本增加多少？

（2）销售量增加一个单位时，总收入增加多少？

解决以上两个问题学生不难发现，第二个问题的运算比较复杂，随着函数复杂程度的提高，计算会更加复杂，将这个问题提前布置给学生：“许多类似实际问题不需要求得△y的精确值，如何方便的求得△y的近似值？”，学生可以利用电脑去网上搜索解决问题的方式：导数可以解决，可什么是导数？自然要先了解极限，这样我们就从极限开始学起.当这个问题最终解决后，就可以介绍边际的概念了.

这个过程正是数学建模思想的具体应用.由此完善学生的数学思维品质，增强数学应用能力，并帮助学生解决各种常规和非常规的问题.培养学生稳定的、基本的、综合的数学素质，拥有这些基本的数学素质，学生将终身受用，到了需要的它们时候，对学生的发展能够起以点带面的重要作用.

教材建设充分体现高职高专教育的特色，淡化理论的完整性、严密性，注重数学的应用性与实践性；淡化数学的逻辑论证，繁杂的计算过程，强化数学的几何说明，重视直观，形象的理解.在体现上述特色的基础上，我们本着结合专业内容，突出培养专业人才的能力，体现“必须够用”为度的原则，大胆尝试了对教材建设的改革.例如，定积分概念的引入，目前教材主要是通过曲边梯形面积的求法，沿着分割、取点、做和、取极限四个步骤完成，但多年教学的感受是（特别是近几年），老师讲得津津有味，学生听得昏昏欲睡.这个在“搞数学”的教师看来经典的数学理论，对“用数学”的高职高专学生来说有点深奥和抽象.为此我们采用的方式是：

引入案例：某化妆品工厂生产某种新型的产品，每天生产 x（件）时的总成本 C(x)（单位元）的边际成本MC=3x2-40x+160，又已知固定成本为4000元.

试求：（1）总成本函数C(x)

（2）产量从50件增加到100件时的总成本.

通过问题（1）引入原函数和不定积分，介绍不定积分的计算（主要借助软件Geogebra）,然后分析问题（2），例题的第二问中，计算产量从50件增加到100件时的总成本，即C(100)-C(50)时，我们可以发现实际参与运算的只是函数x3-20x2+160x，也就是边际成本MC=3x2-40x+160的原函数，为此我们可以将这个过程记作：

总之，通过高职高专经济应用数学精品课的建设，为经管类课程的教学提供数学支持，发展学生善于面对新问题、善于研究新问题的能力，使得经济应用数学的价值让学生看得清清楚楚，从而产生自我学习经济应用数学的需要.

〔1〕陈怀琛.论工科线性代数的现代化与大众化[J].高等教育研究，2012（2）：37-38.

〔2〕吴华,周明.GeoGebra环境下基于APOS理论的数学概念教学研究[J].数学教育学报,2013（2）：87-89.

〔3〕亚当斯（美）,哈斯（美）.微积分之屠龙宝刀[M].长沙：湖南科技出版社，2004.5.

〔4〕云连英，汪荣伟.高职院校高等数学精品课程建设的研究与实践[J].职业教育研究，2008（2）.