基于随机过程的设备性能可靠性预测

莫协强

由于在现实生产生活中各行各业各种事物都具有一定的空间形式和数量关系，所以这种敏感不仅局限在数学思维品质，而且属于社会行为品质了，它的表现形式努力使外界现象数学化，注意现象的数学方面，注意空间和数量关系以及函数间的依赖关系。特别是对于随机过程的分布函数来说，其在生产生活的应用非常广泛，例如，在工业工程中设备性能的可靠性预测和故障排除方面的应用。以下将结合实践中的设备性能可靠性预测与随机过程的分布函数之间的关联性进行阐述[1]。

一、随机过程的概述

（一）随机过程的概念

在许多实际问题和工程中，我们不仅需要研究一个或几个变量，而且还要研究一族无限多个随机变量，例如，为描述系统的随机运动或工程中随机现象的变化过程，我们必须引进依赖于时间参数的随机变化量，也就是依赖于时间参数的一族随机变量，这就产生了随机过程这一概念，例如，以X（t）表示某电气监测装置在累积开机时间(0，t)内出现的故障数，对于每一个固定的时刻t(t＞0)，X(t)是一个取非负整数值0，1，2，……的随机变量，随着t的变动，得到了一族无穷多个相互有关的，且均依赖于时间 t的随机变量 X（t）(t＞0)，X（t）即为随机变量。又如，设某一运用中的电气设备在任一时刻只能于正常、异常和故障三种状态之一，分别记为2，1，0，若以Y（t）(t≥0)，表示在t时刻系统所处的状态，则对任意固定的t≥0，y(t)是一个只能取 0，1，2三个值的随机变量，而随机变量族y(t)(t≥0)就描述了该设备在运用中整个过程，Y（t）即为一随机过程[2]。

（二）随机过程的统计描述

随机过程在任一时刻的状态是随机变量，因此，可以用随机变量的统计表述方法来表述随机过程的统计特性。以下是随机过程的分布函数族。

给定随机过程{X(t),t∈T}，对于每一个固定的t∈T，随机变量X（t）的分而函数一般与t有关，记为

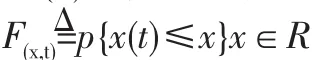
称为随机过程{X(t),t∈T}的一维分布函数，而{F(x,t),t∈T}为一维分布函数族。 一般地，对 n(n=2,3,L)个不同时刻，t1，t2，t3,Ltn∈T引入n维随机变量{x(t1),x(t2),L,x(tn)}，它的分布函数记为

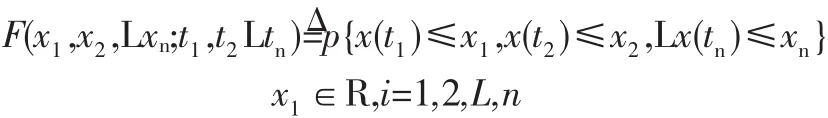
我们称{F(x1,x2,Lxn;t1,t2,Lxn),t∈T}为随机过程{X(t),t∈T}的n维分布函数。

当n取方充分大时，n维分布函数族能够近似地描述随机过程的统计特性，n取愈大，则n维分布函数族描述随机过程的特性愈趋完善[3]。

二、基于随机过程的设备性能可靠性预测

（一）马尔可夫过程

有很多工程现象遵从如下演变原则：由时刻系统或过程所处状态，可以决定该系统或过程在时刻t=t0。所处的状态，而无需借助于以前系统或过程所处状态的历史资料。例如，电力设备的运行状态(用可靠度来描述)，如果只与上次设备的修理状态有关，而与更前面几次设备的修理状态无关。又如研究某设备的绝缘特性，如果现在时刻的某绝缘特性指标已知，则未来某一时刻的该绝缘特性与现在的绝缘特性指标有关，而与这之前的任一时刻的绝缘特性情况无关等等。这就是统计规律上所说的无后效性。用更通俗的话说就是已经知道过程“现在”的条件下，其“将来”不依赖于“过去”。这种已知时刻t系统所处的状态下，在时刻t以后，系统的变化情况与以前系统所处的状态无关的随机过程称为马尔可夫过程[4]。

设随机过程{X(t),t∈T}的状态空间为I，如果对时间t的任意 n 个数值 t1＜t2＜L＜tn，n≥3,ti∈T， 在条件 X(ti)=xi，xi∈I，i=1，2，Ln-1 下，X(tn)的条件分布函数恰等于在条件 X（tn-1）=xn-1下 X（tn）的条件分布函数，即

当n=1，即由ai状态经过一步转移到aj状态的概率为一步转移概率。

例如，讨论单设备维修系统的转移概率，这是个最简单的维修系统，设X（t）表示时刻t系统所处的状态，当设备工作时，系统处于工作状态即X（t）=0，当设备发生故障时，系统牌故障状态，即。

系统从t=0时刻开始工作，经一段时刻发生故障，系统即处于故障修理时刻，经一定时刻设备修复后又立即投入正常工作状态，如此形成故障与工作状态不断交替进行，显然是{X(t),t≥0}是一个随机过程，即设备在正常与故障的相互状态转移过程只与现在所处的状态有关，而与以前的状态转移无关，这过程是一个时间连续，状态空间有限a={0，1}即的马尔可夫过程[5]。

若讨论设备的故障分布服从指数分布，因此系统的状态转移概率只与状态 a{0，1}和时间的间距 Δt有关，因而{X(t),t＞0}是一个齐次马尔可夫过程。设系统的寿命θ和维修时间η分别服从如下分布

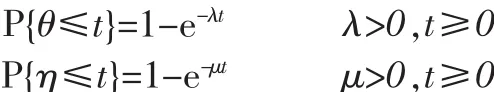
且设备修复与新的一样的寿命分布，和相互独立。

例如，对于某设备组成各部分和安全装置的安全要求以及安全信息的顺利传递来实现的。设备的基本使用功能是在建筑物内垂直升降运输人员和物料。这是由设备合理的结构形式和各组成零件、部件具有足够的机械强度来保证的，即在额定满载情况下，考虑全部静载荷、动载荷，以及意外情况采用紧急措施所产生的载荷作用，不应发生破坏。因此在这种状态下应用随机过程的分布函数可以得出如下的模型，即在设备的可靠性预测当中，要将设“0”表示系统处于正常状态，“1”表示系统处于故障状态；P00表示系统保持于正常状态的概率；P01表示系统从正常状态向故障状态转移的概率；P10表示系统从故障状态向正常状态转移的概率；P11表示系统保持在故障状态的概率[6]。

上世纪20年代，在美国首先实行了预防性的定时维修，即在设备运行，使用到某周期之后，就对设备进行拆卸检查，更换部分零部件，以此预防设备故障的发生。这种防患于未然的定时维修方法减少了设备故障和生产中事故的发生，提高了企业的生产效益。这种维修方法，显然优于那种“不坏不修，坏了才修”的事后维修方法。因此这种定时维修方法的明显优点和产生的效益，使得它迅速被世界各地所采用。此时设备的变化情况与之前设备所处的状态无关的随机过程就可以用来进行分析。

系统或设备在使用中，主要处于运行使用状态和因故障的停运进行检修状态，这两种状态不断循环，构成了设备整个运行使用过程，我们称设备的这种工作状态与停运检修状态之间的循环过程为更新状态，设备每经过一次修理，称为一次“更新”。随着设备维修技术的不断发展，特别是设备群控技术的发展，客观上要求设备的控制系统精确地了解每台设备的载荷量，才能使设备的调度运行达到最佳状态。因此，传统的开关量载荷信号已经不能适用于群控技术，现在很多设备采用电磁式称量装置，为设备控制系统提供连续变化的载荷信号。这样一方面可以方便群控系统进行调度，另一方面可以将载荷信号传递给设备的拖动系统，在设备起动和运行期间调节供给曳引机的电流，调节曳引机的转矩，保证设备的正常运行。这种维修保护装置应用非常广泛、价格低、安全可靠，但更换维修较繁琐，这是装在设备上的超载装置，活动地板四周与设备之间保持一定间隙，随着设备承受载荷的不同，会微微地上下移动。当设备超载时，会使活动地板下陷，将开关接通，给出设备相应的控制信号。通过眼看、耳听、触摸等感观手段来判断为主，最多辅以简单检测设备(如电工使用万用表)，进一步判断、处理和修复故障。此阶段维修仅是一门操作技艺，其工作主要目的是排除故障。维修过程缺乏理沦支持，主要是依靠经验的传授和积累。显然这也符合当时设备的工艺水平和生产发展的实际情况。随着工业化的进步，生产力有了较大的发展，尤其是第一次世界大战之后，工厂企业生产力大为提高，开始出现了流水线生产和连续性作业，仟何生产线作业中断，将造成较大的经济损失[7]。

（二）更新理论

更新理论是研究维修系统的更新过程的一种基本原理和方法，应用于研究零部件的更新，确定维修周期、制定试验程序等。由一批相同零部件组成的单部件设备的更新过程。该设备从时刻T0=0开始工作，当设备中某一零件故障，就立即换上一个新的，并假定更换后立即工作，故系统可一直继续不断地工作。于是，系统中各个零件后发生故障的时间的关系为

式中，Tn——第n个零件的故障时间，也是第n次更新时间（在此时间内，有n个零件故障并予以更换）。

因此， 第 n 个零部件的寿命 τn=Tn-Tn-1， 这些寿命（τ1，τ2，L，τn）是非负随机变量，分布相同且相互独立，第n次更新时间为 τn=τ1+τ2+L+τn

我们称上述时间序列T0≤T1≤T2≤LTn≤L为更新过程。

若 T0≤t≤Tn+1，则在时间（0，t）之间有 n 个零件故障，设 N(t)表示更新次数，即 N(t)=n，这样在（0，t）时间内有两个随机变量，更新次数N(t)和第n次的更新时间T，前者为有离散型随机变量，其值为正整数0，1，2，……，后者为连续型随机变量，其值为任意非实数，所以，在一定的t条件下它们之间的关系，根据概率定义有

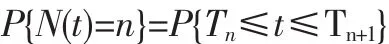
因此设，

式中Fn(t)为故障率F(t)的n次卷积。

预防性维修通常是对设备进行检查、测试，在发现异常或故障时予以消除，防止事故、故障的发生，使设备保持在规定的状态下所做的各项维修活动。预防性维修工作一般包括外观检查，清洁，机械部分的润滑和调整，电气部分的测试和调整，装置的拆修及不合格元部件的更换等。预防性维修活动的企图是消除故障的隐患，确保设备在运行使用过程中不发生故障，从而避免造成更大的损失，做到防患于未然。其活动的时机是在故障发生之前进行，这种维修方法一般用于故障后果会危及安全或影响功能的实现和任务的完成，或者故障会造成较大经济损失和社会影响。

[1]苏文胜，苏永共.灰色─马尔柯夫模型在接发列车事故预测中的应用研究[J].中国安全科学学报，1996，（11）

[2]谢贤平，李怀宇，赵梓成.事故预测专家系统（AFES）的设计[J].劳动保护科学技术，1994，(6)

[3]王贤.“引火烧身”及其它设备内部安全动火[J].劳动保护，1994，（11）

[4]颜炳发.浅谈化工工艺和设备安全性评价[J].黑龙江科技信息，2011，(17)

[5]路立军.浅谈化工设备检修中的动火安全措施[J].设备管理与维修，2000，(11)

[6]郭建波，赵勇，齐照东.铁路事故研究现状及应用[J].工业安全与环保，2005，(3)

[7]黄郑华，李建华，华杨.化工设备检修中的火灾爆炸事故原因分析[J].安全、健康和环境，2005，(12)