等压力梯度曲面压缩系统性能参数化分析
潘 瑾,金 峰,张堃元
(南京航空航天大学 a.金城学院;b.能源与动力学院,南京 210016)
进气道是吸气式发动机的重要部件之一,有轴对称压缩[1]、二维平面压缩[2]、侧压式[3]、三维压缩[4-6]等多种压缩方式,其压缩面的设计具有至关重要的作用。一般来说,对超声速气流的压缩离不开激波压缩或等熵压缩波的压缩。目前公认的进气道设计理念(即压缩面的配波理论)主要是经典的K.Oswatitsch等强度激波理论、等熵压缩理论等。
传统的压缩方式如斜楔压缩、锥形压缩甚至等熵压缩,在应用于高超声速进气道设计时均存在各种各样的问题。例如:多级斜楔压缩损失大,局部压力梯度大;等熵压缩虽然损失小,但压缩面过长,沿流向压力梯度的变化大,使得高超声速进气道不仅长度长、质量大、冷却难,而且摩阻较大。文献[7]提出一种新概念非常规弯曲激波压缩型面的设计方法,并将其运用于二维进气道设计中。采用弯曲激波压缩系统作为进气道的外压缩面,在减小压缩面附面层分离、缩短进气道压缩面长度和提高进气道非设计点性能等方面均有一定的优越性。
本文对曲面压缩系统做了进一步的研究。依据文献[7]的设计理念,采用小折线构成弯曲压缩面,并约束各小折线的壁面压力为等压力梯度变化。通过设计参数的调整,得到不同曲率的等压力梯度曲面压缩系统。在一定的来流条件下,分析了设计参数对曲面压缩系统的出口性能参数及所形成的弯曲激波的性能影响。由于超声速进气道多采用设计点马赫数波系封口(即在设计点等熵压缩波或激波交于一点),因此,给定的曲面压缩系统在超声速来流条件下,如何确定其弯曲激波的形状从而满足激波封口要求是设计人员最关心的问题。本文根据二维无粘膨胀波和激波理论,通过编程计算得到等压力梯度曲面压缩系统及其弯曲激波形状、波后气流参数和壁面气流参数,并进一步拟合出等压力梯度曲面压缩系统和弯曲激波型线的近似计算公式,为等压力梯度曲面压缩系统在进气道设计中的应用奠定了基础。
1 等压力梯度曲面压缩系统的模型和试验结果
1.1 等压力梯度曲面压缩系统当地压比分析
等压力梯度曲面压缩系统沿流向单位距离升压比的计算如图1所示。根据“三角形相似,对应边成比例”的性质,可以得到以下关系式:

则
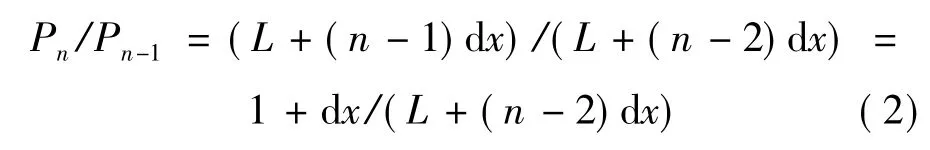
由式(1)和式(2)可知,沿流向随着n的增加,当地压比逐渐减小。由此可见,虽然按照dP/dx=C设计的曲面压缩系统沿压缩面流向每一微段dx的压力增量dP均相同,但每一微段dx前后的压比(P+dP)/P却并不相同,沿流向呈现下降的趋势,这显然对保持壁面附面层的稳定有一定的益处。因此,本文选取等压力梯度曲面压缩系统作为曲面压缩研究的初步研究对象。

图1 等压力梯度曲面系统沿流向单位距离升压比的计算方法
1.2 等压力梯度曲面压缩系统模型
所设计的曲面压缩系统在初始阶段均为6°斜楔,后为弯曲压缩面,斜楔与弯曲型面光滑连接。弯曲压缩面总压缩角为20°。设计参数选取参考南航 Ma5.3/3.85小型高超风洞[8]试验来流条件,即:来流马赫数为5.3(假设空气的比热比1.4保持不变),来流总压为0.7 MPa,总温为420 K。
由于弯曲压缩面初始斜楔的存在,后续曲面压缩型面的设计条件可以看成是来流经过初始斜楔激波压缩后的气流条件。
图2为所设计的等压力梯度曲面压缩系统的风洞试验结果。由试验结果可见:设计点的壁面压力符合等压力梯度变化,与数值模拟结果相吻合;同时纹影照片清晰地显示了所设计的曲面压缩系统形成弯曲激波。
2 等压力梯度曲面压缩系统的数值分析
2.1 弯曲激波压缩系统的理论分析
弯曲激波压缩系统由一个特殊的凹曲面和由此曲面形成的内凹弯曲激波组成。超声速气流流经此凹曲面时,受到连续的压缩扰动,从压缩面产生一系列的压缩波并依次相交,逐步形成内凹的变强度弯曲激波,即弯曲激波压缩系统的核心所在。依据同侧激波相交原理,探讨了如何进行弯曲激波的近似计算。

图2 等压力梯度曲面压缩系统的风洞试验结果
假设给定一个能产生弯曲激波的弯曲压缩面。在压缩面上,依次取出间隔很小的离散点,连续的曲面可以看成是由这些点连成的微元直壁组成。超声速气流流过曲面时,由于压缩过程非常微弱,因此可以近似地认为每一点都将发出一道等熵压缩波。对相邻的两道等熵压缩波进行同族波相交的单元计算,可以得到沿壁面的流动参数、激波上各点坐标和波后参数。由于这些微段可以取无限小,且气流转角非常小,因此在编程数值计算中可以不考虑两波相交产生的滑移面以及反射波对下游流场的影响。如果这些微段为有限长,那么该处理方式就是某种程度的近似。研究表明,取微段为某种合适的尺度的处理方式具有精度高和简洁的特点。
2.2 设计参数对等压力梯度曲面压缩系统性能的影响
按等压力梯度设计的曲面压缩面型面由以下设计参数决定:来流马赫数Ma、来流静压P,初始斜楔长度L0、初始压缩角δ0、总压缩角δ和等压力梯度C。据此进一步确定曲面压缩面所形成的弯曲激波形状。
假设所研究的等压力梯度曲面压缩系统的总压缩角 δ=15°,则可变参数只有 Ma、P、L0、δ0以及C。每次只改变一个设计参数,得到的等压力梯度曲面压缩系统出口压比和总压恢复详见表1。
从表1可以发现:当设计曲面只有初始压缩角不同时,出口压比最大相差0.193 2,总压恢复最大相差0.065 4;当设计曲面只有初始斜楔长度不同时,出口压比最大相差0.061 5,总压恢复最大相差0.028 1;当设计曲面只有来流马赫数不同时,出口压比最大相差4.045 2,总压恢复最大相差0.184 8;当设计曲面只有来流静压不同时,出口压比最大相差0.199 2,总压恢复最大相差0.031 7;当设计曲面只有等压力梯度值不同时,出口压比最大相差0.155 6,总压恢复最大相差0.005 5。由此可见:在所讨论的等压力梯度曲面压缩系统设计参数中来流马赫数Ma对等压力梯度设计曲面压缩系统的出口性能参数影响较大,其次是来流静压P,影响最小的是初始斜楔长度L0和等压力梯度值C。
同样假设所研究的等压力梯度曲面压缩系统总压缩角 δ=15°,可变参数只有 Ma、P、L0、δ0以及C。每次只改变一个设计参数,研究等压力梯度曲面和其所形成的激波型线的变化。
图3给出了相同总压缩角δ=15°时,设计参数对等压力梯度设计型面及其所形成的弯曲激波形状的影响。图3中壁面wall1对应的激波型线是shock1。依此类推,壁面wall4对应的激波型线是shock4,分别对应各设计参数由小到大的变化。
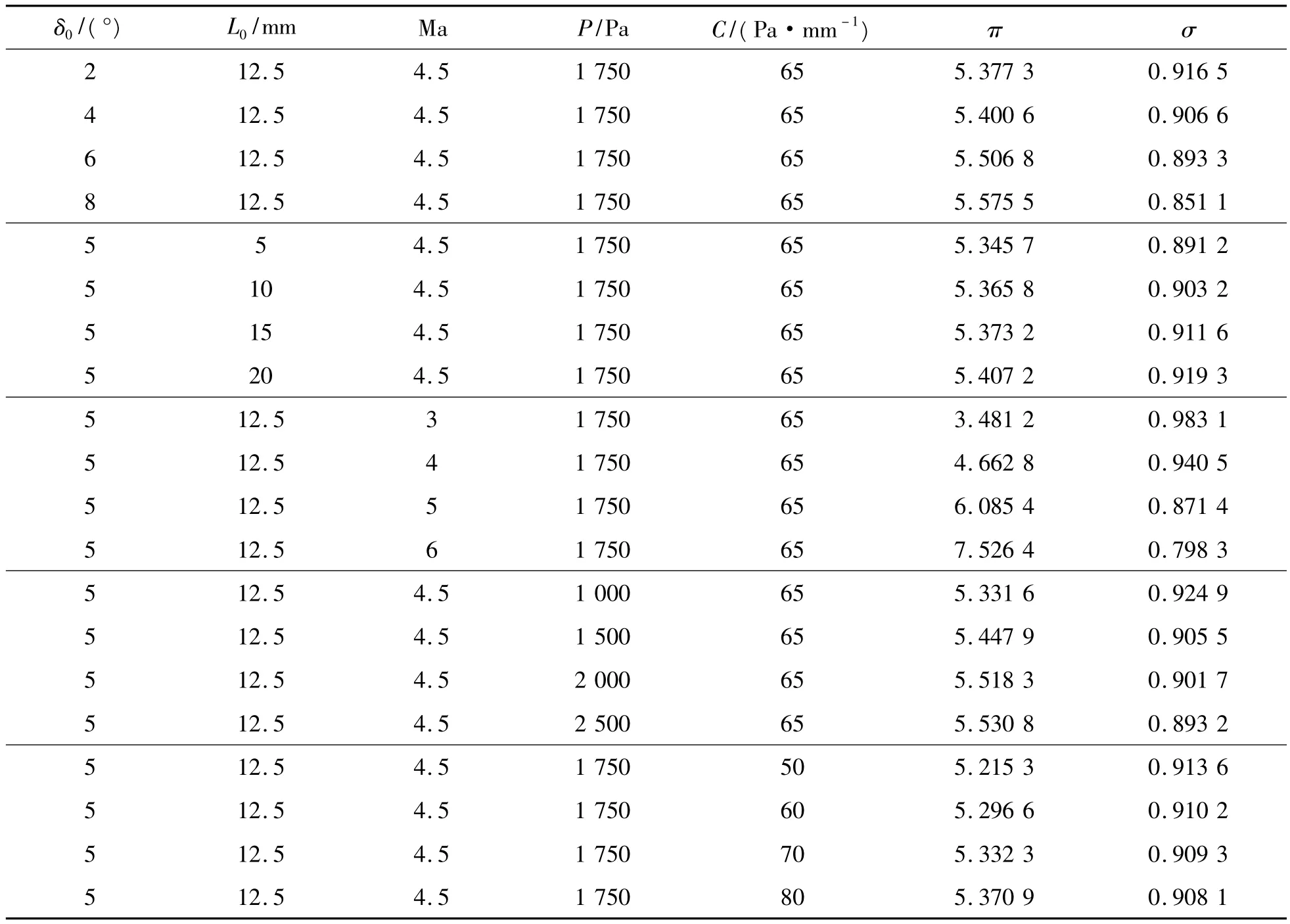
表1 等压力梯度曲面压缩系统出口压比和总压恢复
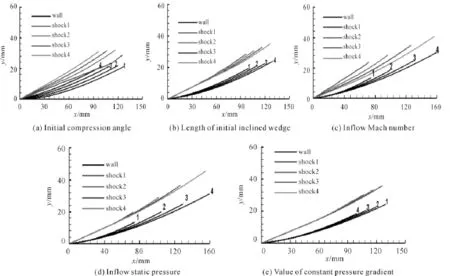
图3 δ=15°时设计参数对等压力梯度设计型面及其所形成的弯曲激波形状的影响
图3(a)给出了初始压缩角δ0的变化对壁面型面及其所形成的激波型线的影响。由图3(a)可知:随着初始压缩角δ0的增大,压缩面长度缩短,所形成的激波曲率增加。究其原因,主要是在总压缩角一定的前提条件下,若初始压缩角增大,曲面压缩角势必减小,导致相同等压力梯度设计的曲面缩短;而初始斜板长度仍然保持不变,那么整个压缩面的长度就会缩短。图3(b)、(c)和(d)分别给出了初始斜楔长度L0、来流马赫数Ma和来流静压P对壁面型面及其所形成的激波型线的影响。由此可知:这3个参数越大,所得到的曲面曲率越小、壁面越长。图3(e)给出了等压力梯度值对壁面及其所形成的激波型线的影响。由此可知:等压力梯度值越大,则壁面曲率越大、壁面越短。在各参数变化过程中,激波型线与其对应的压缩面呈现出同样的变化规律。
2.3 等压力梯度曲面压缩系统壁面及其弯曲激波拟合公式
为方便工程应用,以来流马赫数Ma、静压P、等压力梯度dP/dx和初始压缩角δ0为自变量,在来流马赫数Ma=3~6、静压P=1 000~2 500 Pa、等压力梯度dP/dx=50~80 Pa/mm和初始压缩角δ0=(5~8)°时,根据编程数值计算的结果,将等压力梯度设计的壁面和其形成的弯曲激波型线运用最小二乘法拟合成以下预估公式:
1)等压力梯度曲面压缩系统壁面的型线公式

其中:

2)弯曲激波型线公式

其中:

2.4 编程数值计算和预估公式的结果比较
图4是取不同设计参数分别采用自编计算程序和拟合公式计算得到的等压力梯度壁面及其弯曲激波型线的比较。所取参数如下:a)来流马赫数Ma=3、静压P=2 500 Pa、等压力梯度dP/dx=80 Pa/mm和初始压缩角 δ0=8°;b)来流马赫数Ma=4、静压P=2 000 Pa、等压力梯度dP/dx=80 Pa/mm和初始压缩角δ0=6°;c)来流马赫数Ma=5、静压P=1 500 Pa、等压力梯度 dP/dx=60 Pa/mm和初始压缩角δ0=5°;d)来流马赫数Ma=6、静压P=1 500 Pa、等压力梯度dP/dx=80 Pa/mm和初始压缩角δ0=7°。
由图4可知:自编程序数值计算和拟合公式计算结果,在本文计算的来流条件下符合较好。说明可以用预估公式代替自编程序进行计算,从而更快捷地得到等压力梯度弯曲压缩面及其激波型线。
为进一步验证预估公式的精度,根据来流马赫数Ma=5.3时试验拍摄到的激波纹影照片,取出激波上的点拟合成激波面曲线,与同样来流条件下拟合公式得到的激波型线进行比较,比较结果见图5。由结果可知,这两条型线基本符合。尽管沿流向的垂直方向存在一定的差异,经计算得到等压力梯度曲面压缩面出口位置处两条型线的纵坐标相对差为4.8%。这可能是由于数值计算为近似计算,未考虑到黏性的影响而造成的。因此,可以方便地用拟合公式来大概预估该公式使用范围内的等压力梯度弯曲压缩面及其弯曲激波面的形状,进而预估采用等压力梯度压缩的二维进气道唇口位置,为这种特殊进气道的初步设计提供了一种简便、准确的预估手段。

图4 不同设计参数下等压力梯度壁面及其弯曲激波型线的比较

图5 激波型线比较结果(Ma=5.3)
3 结论
本文对等压力梯度曲面压缩系统进行了初步研究,给出了等压力梯度曲面压缩系统的设计方法并进行试验验证。数值分析了来流马赫数Ma、来流静压 P,初始斜楔长度L0、初始压缩角 δ0、总压缩角δ和等压力梯度C对等压力梯度曲面压缩系统的出口性能及其壁面和激波型线的影响,初步得到以下结论:
1)等压力梯度曲面压缩系统初始压缩角δ0对其性能及所形成的弯曲激波型线影响较大。
2)初始斜楔长度L0、来流马赫数Ma和来流静压P越大,所设计的等压力梯度曲面压缩面型线曲率越小,型线越长,唇口位置越后。初始压缩角δ0和等压力梯度值C越大,所设计的等压力梯度曲面压缩面型线曲率越大,型线越短,唇口位置越提前。
3)在本文计算条件范围内,得到了预估等压力梯度弯曲压缩面及其弯曲激波面形状的拟合公式,为采用等压力梯度压缩的二维新概念进气道的初步设计提供了一种简便、准确的预估手段。
[1]王健,李宏东,朱守梅,等.冲压发动机用轴对称进气道设计和试验[J].推进技术,2009,30(6):682 -686.
[2]张晓嘉,岳连捷,张新宇.大内收缩比二元高超声速进气道波系配置特性[J].推进技术,2012,33(4):505-509.
[3]金志光,张堃元.高超侧压式进气道高焓脉冲风洞实验[J].推进技术,2005,26(4):319 -323.
[4]肖雅彬,岳连捷,龚鹏,等.三面压缩式高超声速进气道流动结构研究[J].实验流体力学,2008,22(2):64-67.
[5]孙波,张堃元,金志光,等.流线追踪Busemann进气道设计参数的选择[J].推进技术,2007,28(1):55-59.
[6]尤延铖,梁德旺,黄国平.一种新型内乘波式进气道初步研究[J].推进技术,2006,27(3):252-256 .
[7]潘瑾,张堃元,金志光.弯曲激波压缩型面的设计及数值分析[J].推进技术,2008,29(4):438 -442.
[8]潘瑾,张堃元.移动唇口变内收缩比侧压式进气道反压特性和自起动性能[J].航空动力学报,2009,24(1):104-109.

