齿轮-凸轮组合机构解析法设计

杨燕珍，苏同克

（1.龙岩学院物理与机电工程学院，福建龙岩364012；2.上海微电子装备有限公司，上海310000）

齿轮-凸轮组合机构解析法设计

杨燕珍1，苏同克2

（1.龙岩学院物理与机电工程学院，福建龙岩364012；2.上海微电子装备有限公司，上海310000）

通过实例分析齿轮-凸轮组合机构，介绍了按给定的轨迹曲线来设计齿轮-凸轮组合机构的凸轮廓线的解析设计方法.

凸轮；齿轮；组合机构

齿轮-凸轮组合机构可实现有任意停歇或复杂运动规律的间歇运动和特殊规律的补偿运动等，是一种正在发展的新型组合机构.其结构紧凑，控制准备并且有效，拥有齿轮和凸轮的特性，能够实现特定的要求以及输出任意的、复杂的运动轨迹.因此，齿轮-凸轮机构在各种机械行业中应用广泛.

本文利用反求设计法实现齿轮-凸轮组合机构的凸轮廓线的设计.以下对该方法进行详细介绍.

1 齿轮—凸轮组合机构的设计

1.1 机构分析

图1所示齿轮-凸轮组合机构是以相啮合的一对齿轮为基础，利用滚子凸轮机构来控制杆CD的运动参数，通过杆AB与杆BC组成的RRR杆组和杆CD与杆CE组成RRR杆组的运动复合实现输入与输出的运动间的关系，从而输出给定轨迹.其中齿轮1与杆AB固联在一起.由于运动轨迹已知，根据A点坐标与E点轨迹可求出杆AB与杆BE的长度；根据机构的总体布置，设计者可预先确定的齿轮1的半径R1、齿轮2的半径R2、杆CD的长度LCD、杆CE的长度LCE、A点坐标、D点坐标、K点坐标等，因此杆AB和杆BE组成一个RRRⅡ级杆组.通过齿轮啮合传动关系由B点的坐标确定可确定G点的坐标.

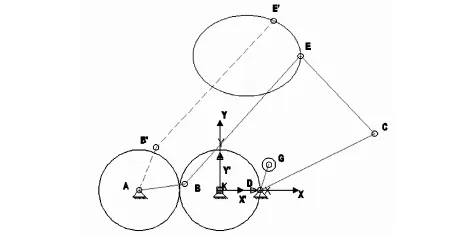
图1 凸轮齿轮组合机构

1.2 设计方法

1.2.1 建立已知轨迹的参数方程

建立坐标系XKY.此时，在XKY中确定E点的轨迹.用一个参数方程来表示E点轨迹坐标，任取一点E0作为起始点，假设E点沿着规定方向运动，并将E点的轨迹曲线任意分割成N个分点，每一个分点对应一个指针I，于是可得出E点轨迹的坐标参数方程：

式中：I=0，1，2，…，N，为了使设计准确，N的数值应该取足够大，一般取凸轮廓线所需点数的10倍左右.

设计中，用到E点的速度以及E点的轨迹坐标.在所设计的凸轮廓线中，只要E点的轨迹不变，那么E点速度的变化就不会对其结果产生影响.因此，可令dI/dt=1,则得出E点的速度为：

1.2.2 确定尺寸

根据设计的实际需要来选择基本尺寸，如图1中所示.根据机构动力学性能及总体需求，适当选取定点A的坐标（XA,YA），齿轮1和齿轮2的节圆半径R1、R2，杆CD的长度LCD，杆CE的长度LCE,杆DG的长度LDG.

由于点A与点E的位置已确定，设计中，取I=1到N，以步长为1，进行循环.每个I调用一个判断语句程序，可得到杆AB和杆EB分别位于拉直共线和重迭共线位置时的最远距离(LAE)max及最近距离(LAE)min，以及相应的指针Imin和Imax.由此可得出杆AB和杆EB的长度：

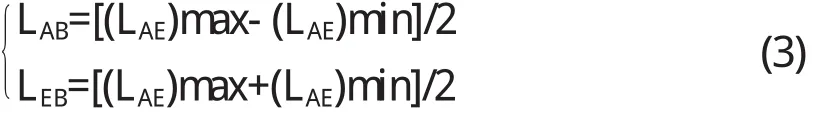
1.2.3 求凸轮在与其固连的动坐标系中的轨迹坐标

取I=1到N，步长取为5进行循环，其中步长取5是为了使I避开Imax和Imin，以避免杆AB和杆EB共线以及无法进行运动分析的一些点.用RRRⅡ级杆组对杆AB和杆EB，进行分析.图1所示，在求解时，实线A、B、E三点逆时针排列和虚线A、B、E三点顺时针排列是不同的装配模式.图中AB为曲柄，由杆AB和杆EB所组成的RRRⅡ级杆组装配模式会在运动过程中发生改变，即杆AB和杆EB两共线的位置处，发生装配模式的改变.装配模式不同，运动分析时，调用杆组的方式也不同.

不同装配模式的判断方式：设齿轮1逆时针转动，在AB、EB的初始位置，如果IminImax，A、B、E三点为逆时针排列，则调用RRR(EBA)（如图1中虚线所示）.这样便可求出运动参数θAB、ωAB和θEB、ωEB及AB、EB的位置.将杆CD和杆CE看成一个RRRⅡ级杆组进行分析,可求出G点坐标，由坐标变换可得G点在X1KY1动坐标系中的坐标：

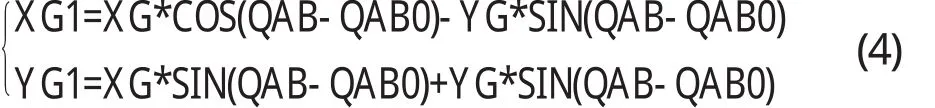
1.2.4 求凸轮实际廓线的坐标XGT、YGT

根据凸轮实际廓线与理论廓线的关系可得出，凸轮实际廓线在坐标系X’BY’中的坐标方程为：

2 实例

建立如图1所示的固定坐标系XKY，其中E点的轨迹为：以点（20,100）为椭圆圆心，长轴为40mm，短轴为30mm的椭圆.A点的坐标为（-60, 0），LCD=95mm，LCE=80mm，LDG=20mm，齿轮半径为30mm，滚子半径为RG=5mm.根据以上设计方法，可求得的凸轮廓线如图2所示.

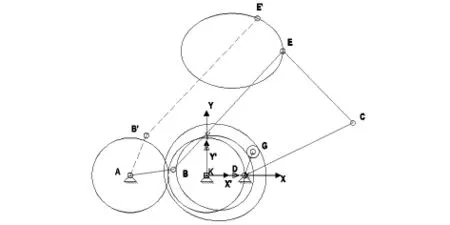
图2 凸轮轮廓廓线图

3 结论

本文介绍了按给定的轨迹曲线来设计齿轮-凸轮组合机构的凸轮廓线的解析设计方法.该方法具有简便、精度高等优点，为齿轮-凸轮组合机构设计提供参考.

〔1〕Watanabe Katsuin,Exact analysis of plant cam mechanisms having errorin kinermatic constants. Nippon Kihai Gakkai ronbunshuc Hen,1993.

〔2〕Xing Yingjie.Recording and processing of planar cure using clothoids(Ind Report)-recording of cam profile with clothoidal interpolation, Tokyo:Seim itsu kogaku kaishi 61&Aug 1995 JSPE,1995,1092-1100.

〔3〕石永刚,徐振华.凸轮机构设计[M].上海:上海科学技术出版社,1995.

〔4〕刁燕,贺红梅.齿轮凸轮组合机构的函数最优综合及动态模拟[J].机械设计,2002.

〔5〕张杰.一种新型内凸轮齿轮组合机构的原理与尺度综合[J].机械设计,2003.

〔6〕陈瑞良,叶仲和.摆动从动件凸轮-连杆组合机构的解析法设计[J].机械设计,2003.

〔7〕郑文纬,吴克坚.机械原理[M].北京:高等教育出版社，1997.

〔8〕叶仲和,蓝兆辉,M R Smith.Mechanisms and Machine theory[M].北京:高等教育出版社, 2001.

〔9〕简兆辉，刘晓敏，梁子新，叶仲和.给定运动规律的齿轮-凸轮组合机构解析法设计[J].机械设计与研究，2009.

〔10〕袁剑雄，李晨霞，潘承怡.机械结构设计禁计[M].北京机械工业出版社，177-181.

TH112

A

1673-260X（2013）12-043-02