单指数模型的稳健回归及实证
谢振中
(邵阳学院理学与信息科学系,湖南邵阳 422000)
0 引言
单指数模型是著名经济学家威廉.夏普于1963年提出的投资组合模型[1],有关该投资组合模型的传统的统计研究和应用取得了很多研究成果,许多国内学者将国外已有的研究成果应用于国内市场进行实证分析,力求对最优资产组合的选择起到指导作用[2][3]。作为投资组合理论中经典的投资组合模型,它是以证券收益率历史数据为基础来度量它们的期望收益和风险的。在现实中,历史收益率数据中往往存在着一些因重大利好或重大利空消息导致的超高或超低收益率,所以当我们用证券的收益率历史数据来估计它们的期望收益和风险时,以此为基础构建的投资组合在长期中就会偏离其实际的投资价值,从而影响到投资组合的决策。具体来说,单指数投资组合模型在进行回归分析时,经典普通的最小二乘法通过极小化残差平方和求得各个回归系数对残差的大小非常敏感,而离群值的存在将直接导致回归残差的异常,进而会影响到回归系数的估计结果,并最终影响投资组合的选择。为了得到单指数模型中长期稳定的关系结构,本文将Huber的稳健回归方法[4]应用到该投资组合模型,作为对传统统计方法的一种补充,并结合我国证券市场的特点,对A股市场进行了实证分析,降低了收益率历史数据中离群值等非正常因素对投资组合决策的影响,得到了证券投资组合的有效前沿。
1 单指数模型
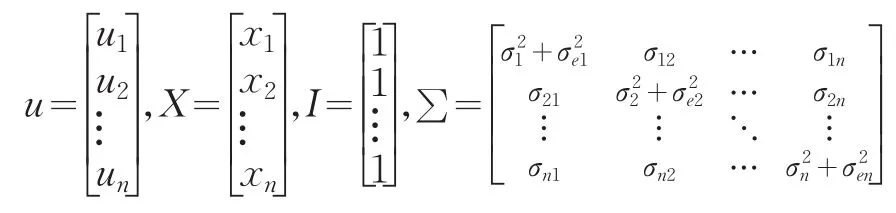
考察一个含有n种资产的投资组合
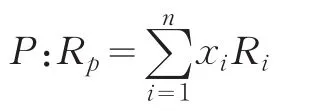
将它的收益率记为Rp,第i种资产的收益率记为Ri,xi表示投资第i种资产所占总投资的比例,收益率Ri是一个随机变量,它的期望收益率记作ui,σij表示资产i与资产j收益率的协方差,那么有
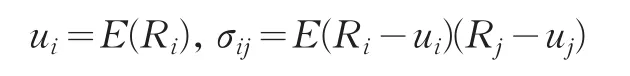
相应地投资组合P的预期收益率up和方差σ2p就分别表示为
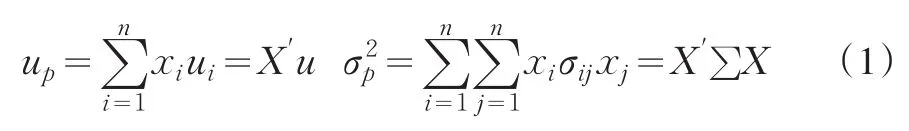
其中u为期望收益率向量,X为权重向量,∑为各资产收益率的协方差矩阵。
威廉.夏普认为,当市场股价指数上升时,市场中大量的股票价格随之走高;相反当市场指数下滑时,大量股票价格也趋于下跌。虽然某些股票较其它股票上升或下跌的幅度要大些,但总地来说都呈现同一趋势的变动。基于这一理论假设,任意证券的收益率与该证券所在市场的某种具有代表性的指数呈线性关系,即

这就是夏普单指数模型,其中Rm表示证券市场指数收益率,为一随机变量,αi表示证券收益率中独立于证券市场指数的部分,βi表示反映Rm的变化对Ri的影响,ei表示误差项,均值为零,即E(ei)=0分别记市场指数收益率Rm和误差项ei的标 准差σm,σei,则由基本假设有cov(ei,ej)=0,说明股票同时系统变动的主要原因是随市场共同变动,不受市场之外的其它原因影响而协同变动,这是单指数模型的核心假设。另外我们还能得到cov(ei,Rm)=0,这说明残差是证券实际收益率与预期收益率的差额,是独立于市场指数的随机变量,与整个市场的运行状况无关。根据这些假设条件可推导出单指数模型下证券的期望收益、方差和协方差。证券的期望收益为E(Ri)=E(αi)+βiE(Rm),方差为协方差为将证券的期望收益、方差和协方差代入(1)
式,得到投资组合的期望收益和方差:

这样,单指数模型(2)的投资组合问题可以通过下述规划模型(3)求解:
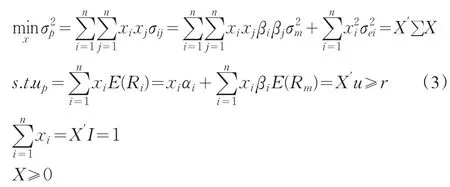
其中X为权重向量,r为投资组合P的预期收益率。并且有
规划模型(3)的经济意义是在市场存在卖空限制条件下,投资者通过一次性满仓操作,使得所构建的投资组合确保收益达到或超过投资者的预期时,所面临的风险最小。如果一个投资组合能在保证一定收益下追求风险的最小化,那么该投资组合被认为是有效的,一个理性的投资者会在投资组合的有效前沿上构建投资组合。
2 稳健回归M估计
传统的统计方法对所研究问题的数据服从正态分布的假定有较强的依赖性,当真正的数据并不是或并不完全是服从正态分布时,如果还按照传统的统计方法来描述我们所研究的问题,就必定会产生偏差,甚至有时这种偏差非常大。研究者对很多数据分布形态的研究表明,正态分布只是一种理论上的分布,实际数据的分布形式偏离正态分布的假定是经常和普遍的,而这种偏离可能会对传统的统计方法的稳健性产生致命的影响,甚至会得出错误的结论,减轻或是避免这种情况的发生就要用到稳健的统计方法。
在建立单指数模型时,如果误差项不服从正态分布,最小二乘法估计的结果就会严重脱离事实,估计的精度也很差,而当样本数据含有离群值数据时,OLS估计(即普通最小二乘法估计)出的残差就不会是正态分布,而往往是偏尾的,其修补的措施并不应该是草率地剔除掉,因为这些离群值数据并不是任何执行错误所致,而是固有的数据变异性的结果,简单地剔除它们,会导致重要的隐藏信息的丢失。当然在回归分析中也不应该与正常数据一样对待,它们出现的概率或频率毕竟很小,合理的做法是采用稳健回归,以消除OLS估计对异常数据的易受影响性,去稳健估计回归模型中的参数。
最常见的稳健回归方法是由Huber在1964年提出的M估计,对于线性模型:
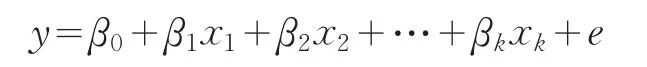
对应的样本模型为:
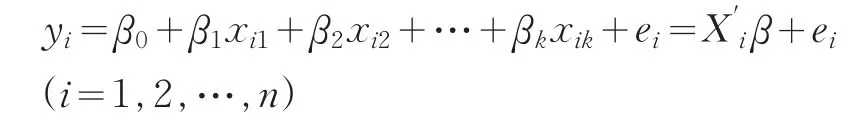
当ρ(ei)=e2i时,则M估计就是OLS估计,即M估计可以看成是OLS估计的扩展。
记ψ=ρ′为函数ρ(t)的导数,则目标函数对参数β求偏导数,并令偏导数等于0,就会得到关于参数的k个方程:
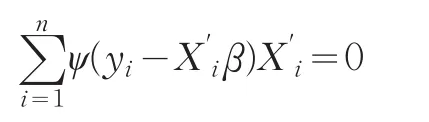
定义权重函数w(e)=ψ(e)/e,记wi=w(ei),这时上述方程可以写为:
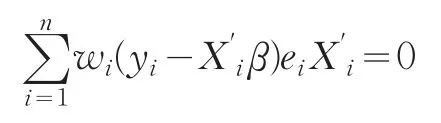
(1)选择初始估计值β(0),例如将LS估计的结果作为初始值;
(2)按此初始值进行迭代,在迭代的第t步,都计算一下上次迭代的残差和相应的权重
(4)重复第2步和第3步,直到估计的参数趋于一致,迭代结束。
选择适当的目标函数ρ和权重函数w(e),让导致残差异常的离群值点的权重变小,残差小的样本数据权重增大,从而减少离群值点对回归分析的影响,实现稳健回归的目的。
稳健回归主要有Huber估计和Bisquare估计两种方法,本文选择Huber估计方法进行实证分析,其目标函数和权重函数如表1:

表1
在Huber估计中,k称为阀值,k值越小,消弱离群值的影响范围越广,离群值的权重越小,这种稳健估计量都对服从正态分布的误差影响小,对不服从正态分布的误差影响大。当k值确定以后,估计的残差越大,它的权重就越小,适当的选择k值,就能保证对离群值影响的处理,例如,在Huber估计中k=1.345。通过比较可以看出,最小二乘法对所有样本的权重都是1;Huber估计对残差接近0的样本权重是1,残差绝对值大于k值的样本,离k值越远,权重越小。它们的权重函数图像如图1所示:
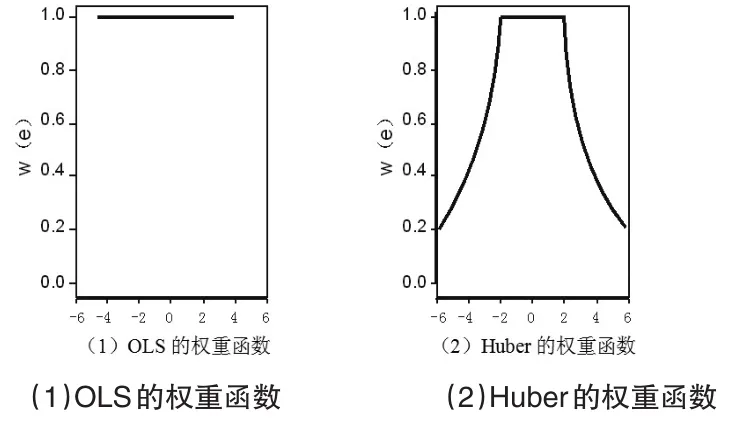
图1 权重函数图像的比较
3 稳健投资组合的实证分析
3.1 稳健投资组合的提出
单指数模型在求解过程中需要进行回归分析,而经典普通的最小二乘法回归时通过极小化残差平方和求得各个回归系数,而这个过程本身就使得回归系数的大小对残差的大小非常敏感,而离群值的存在将直接导致回归残差的异常,进而会影响到回归系数的估计结果,并最终影响投资组合的选择。因此必须将稳健统计的思想和方法融入到该投资组合模型中,利用稳健回归的方法进行稳健回归分析[5],根据历史收益率数据来估计模型中参数αi、βi和σei的值,并在此基础上求解投资组合规划模型。
3.2 样本股票和样本区间的选取
3.2.1 样本股票的选取
在选取样本股票时,为了使样本股票具有代表性,尽量从不同行业和不同地区进行选取。相对于大盘股而言,小盘股更容易受政策消息面等因素的影响,从而使股价在短期内呈现大起大落的态势,具体表现为收益率序列中存在一些异常数据。从长期来看,在一定程度上会对投资者投资组合的选择产生误导。基于以上考虑,从沪市中小盘板块中选取10只股票作为投资组合的研究对象,详见表2。考虑到配股、送红股等因素对股票价格的影响,我们利用大智慧软件的自动复权功能,下载这10只股票复权后的周收盘价,计算出它们的周收益率,得到十只股票的历史收益率序列(表略)。
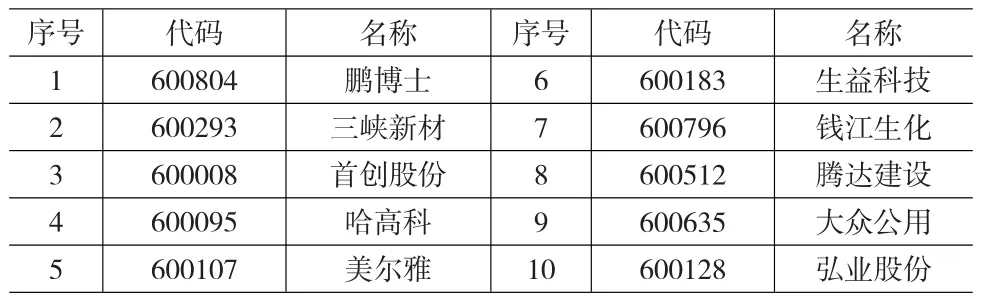
表2 样本股票
3.2.2 样本区间的选取
样本区间选择2010年1月1日年至2011年12月31日,之所以把样本区间定义两年,主要考虑到期间人民币存款利率、存款准备金等进行了多次调整、通货膨胀以及国际局势如美债危机、欧债危机等因素的影响,使得历史收益率数据中存在一些离群值,利用这期间的历史数据来估计参数并构建投资组合模型对现实操作具有一定的指导意义。
3.3 实证检验及结果分析
基于以上稳健回归方法,根据历史收益率数据,估计出单指数模型中的参数,进而求解其投资组合模型,得到它的有效前沿,对比分析OLS、Huber两种不同估计方法对最终结果的影响。首先以样本期间中上证综指周收益率为解释变量,依次以10只样本股票的周收益率为被解释变量,对单指数模型中参数αi、βi分别通过OLS估计方法和Huber稳健估计方法进行估计,并估计出相应的误差项标准差σei,本步骤必须使用迭代法对方法求解,其计算过程通过迭代软件V1.0实现,计算结果如表3所示:
从表3可以看出,Huber估计方法得出的σei都要明显小于OLS方法估计得出的σei,因而可以认为稳健回归方法的拟合效果要明显好于OLS方法。这是由于稳健回归方法在估计过程中对数据中离群值赋予较小的权重,从而减少了离群值对回归结果的影响。
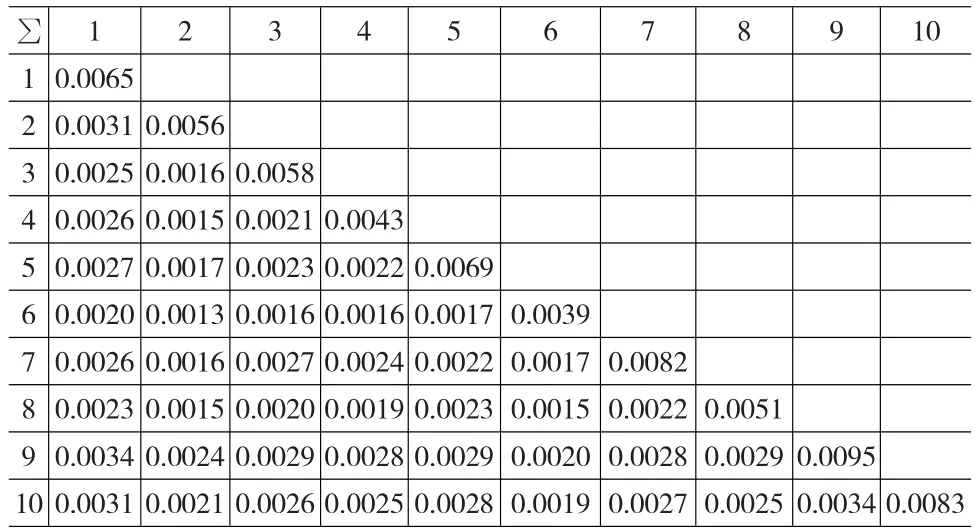
表5 OLS方法得到的协方差矩阵∑
下面根据估计出来的参数αi、βi和σei的值以及通过上证综指收益率数据计算出E(Rm)=0.005243和σ2m=0.002325来构建投资组合模型中的期望收益率向量u和各资产收益率的协方差矩阵∑,相应结果见表4—表6:
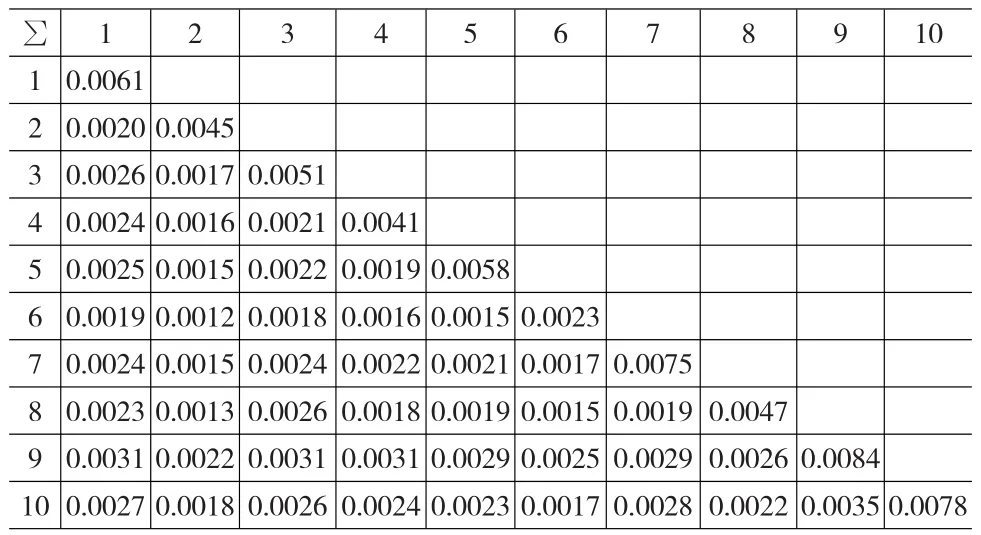
表6 Huber方法得到的协方差矩阵∑
将上述计算结果带入到单指数投资组合规划模型(3)中,通过非线性规划求解得到投资组合的有效前沿,其规划求解通过Matlab6.5软件来实现,见图2,图中纵轴表示投资组合的预期收益率,横轴表示投资组合的标准差,它衡量着投资组合的风险。虚线表示用OLS方法估计得到的投资组合的有效前沿,实线表示用Huber方法估计得到的投资组合的有效前沿。
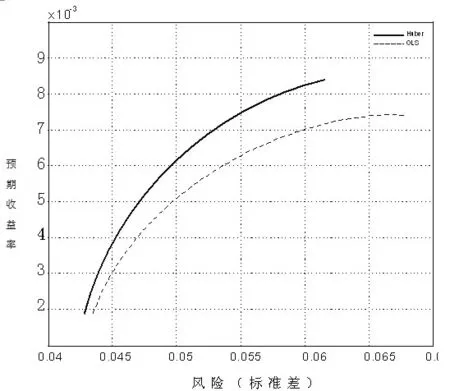
图2 投资组合有效前沿
从图2可以发现,利用Huber方法最终得到的投资组合有效前沿比用OLS方法得到的投资组合有效前沿向左上方移动了一定的幅度,这一结果正好与稳健回归方法中Huber估计的权重函数是一致的,相比较而言,Huber方法的权重随残差ei绝对值的不断增加,权重函数不断趋于0,因此,当数据中存在一些离群值的时候,Huber方法对于离群值的修正作用得到了有效的体现,即在相同的预期收益率下,由Huber稳健估计方法得到的最优投资组合的风险要小于传统OLS统计方法得到的最优投资组合的风险。
4 结论
从实证分析我们可以看到,将稳健回归方法引入到夏普单指数投资组合模型,通过稳健回归先估计出单指数模型中的参数αi、βi的值,再构建期望收益向量和协方差矩阵,建立规划模型,能从一定程度上降低由于短期行情带来的超高或超低收益率历史数据等离群值对投资组合有效前沿带来的影响,从而使我们构建的投资组合在长期中能体现其真正的投资价值,达到预期收益相同而风险最小的目的,说明稳健统计方法与投资组合理论相结合的可行性,这对长期投资者的股票组合投资决策具有现实指导意义。
[1]威廉,夏普.资产组合理论与资本市场[M].北京:机械工业出版社,2001.
[2]熊和平.投资组合协方差矩阵的性质与最优组合的选择[J].中国管理科学,2002,(10).
[3]田兵,陈晓红.基金投资中的单指数模型[J].中南工业大学学报,2001,(4).
[4]P.J.Huber.Robust Estimation of a Location Parameter[J].Annals of Mathematical Statistics,1964,(35).
[5]滕素珍.稳健回归分析[J].大连理工大学学报,1991,(6).

