资源三号测绘卫星三线阵影像高精度几何检校

蒋永华，张 过，，唐新明，祝小勇，秦前清，李德仁，付兴科

1.武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079；2.国家测绘地理信息局 卫星测绘应用中心，北京 100830

1 引 言

目前国产光学卫星的无控、带控几何精度与国外同类卫星差距甚远，其中的一个主要原因是国内对在轨几何检校研究的不多。在外方位元素检校方面，国内学者提出过偏移矩阵［1］、姿态系统误差检校［2－3］等方法，但利用这些方法完成外方位元素检校后，国内在轨卫星的无控定位精度普遍仍在百米量级；而国外如SPOT5、IKONOS等检校后的无控定位精度均优于50m，Geoeye、WorldView－1、2无 控 定 位 精 度 更 在10m 以内［4－11］。在内方位元素检校方面，国内学者研究过航天卫星的内方位元素建模［12－13］，却少有针对国产卫星的试验验证及模型精度评估。在没有对相机畸变进行标定情况下，国产卫星影像即使采用足够数量控制点，其几何纠正精度仅能达到3～4像素［14－15］，而国外卫星影像经过内方位元素检校后的几何纠正精度普遍在一个像素以内［4－11］。

资源三号测绘卫星是我国第一颗民用立体测绘卫星，用于生产全国基础地理信息1∶5万测绘产品及1∶2.5万或更大比例尺地图的修测和更新，开展国土资源调查和监测［16］。资源三号搭载4台相机，一台2.1m地面分辨率的正视相机、两台3.6m分辨率的前视、后视相机和一台分辨率5.8m的多光谱相机。

表1详细列出了资源三号载荷信息。为了保证幅宽，资源三号三线阵相机和多光谱相机均采用多CCD拼接，图1中为资源三号三线阵相机焦面简图，其中正视相机采用3片CCD拼接，重叠像素约为23个，前后视相机采用4片CCD拼接，重叠像素约为27个。

图1 资源三号三线阵相机焦面简图Fig.1 Diagrams of ZY－3three－line camera focal plane

在轨几何检校是测绘卫星实现立体测图的关键。通过在轨几何检校消除资源三号卫星在轨成像系统误差，是保障资源三号卫星影像几何质量、完成立体测图任务的关键［17］。本文通过在线阵推扫式严密成像几何模型中引入用于消除载荷安装、姿轨测量等系统误差的偏置矩阵和多线阵CCD内方位元素模型，构建了用于在轨几何检校的严密成像几何模型，为了消除姿态抖动等对内方位元素检校的影响，提出了多检校场检校的几何模型，并利用该模型和华北多个区域的1∶2000控制数据完成了资源三号三线阵相机的在轨几何检校，利用带有靶标的三线阵数据验证了几何检校的精度。

2 在轨几何检校的严密成像几何模型

严密成像几何模型的建立是在轨几何检校的基础。文献［18］根据星载光学推扫成像几何建立了严密成像几何模型，即

式（1）能最为精确地表达资源三号卫星三线阵相机成像几何，但却由于模型参数相关性，不适宜作为用于几何检校的严密成像几何模型。

2.1 引入偏置矩阵的严密成像几何模型

星载光学推扫成像中，轨道误差与姿态误差影响几何定位精度的特性不同［19］，但是两者可依据一定的几何关系进行等效处理［20］。

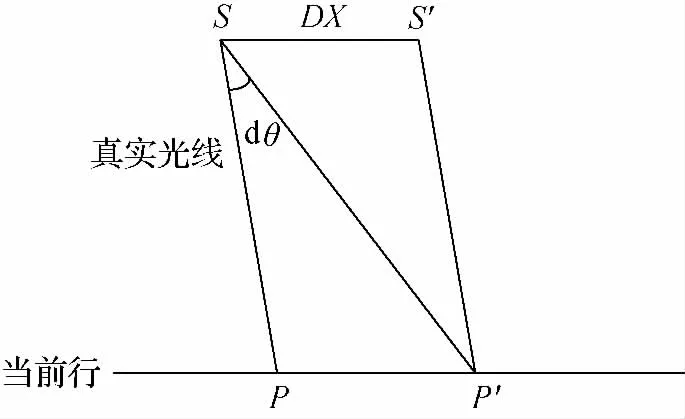
图2 轨道误差与姿态误差等效关系Fig.2 The equivalent relationship between the satellite position error and the attitude error

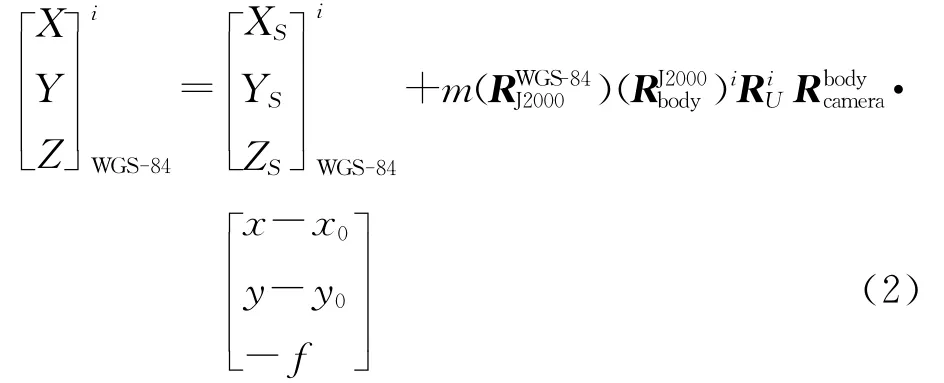
式中，上标i表示第i景对应参数。

2.2 多线阵CCD拼接的内方位元素建模

对公式（2）引入内方位元素误差引起的像点偏移（Δx，Δy），式（2）可化为

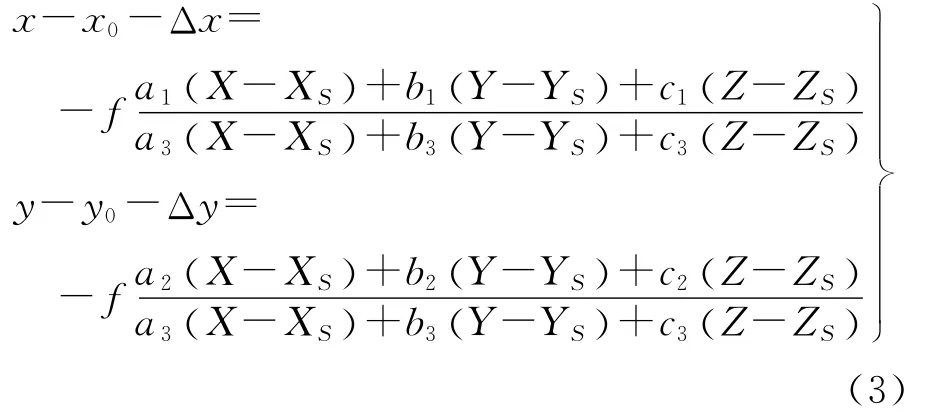
2.2.1 主点偏移误差

假定主点x0、y0的平移误差为 Δx0、Δy0，则其引起的像点偏移为等量平移，即

2.2.2 主距误差

对式（3）主距f求偏导，得主距误差Δf引起的像点偏移

2.2.3 探元尺寸误差

假定探元s0位置为主点位置，则对线阵CCD上任意探元s，其像主点坐标为

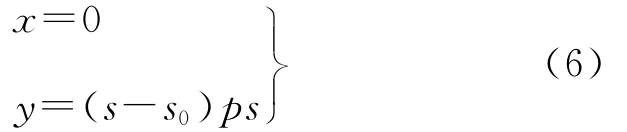
式中，ps为探元尺寸大小。

假定探元尺寸误差为Δps，则由公式（6）知

2.2.4 CCD旋转误差

由于卫星发射时的受力及在轨物理环境的剧烈变化，多CCD排列会发生变化，主要是阵列旋转变化。如图3即为在轨后线阵CCD阵列排列的旋转变化。

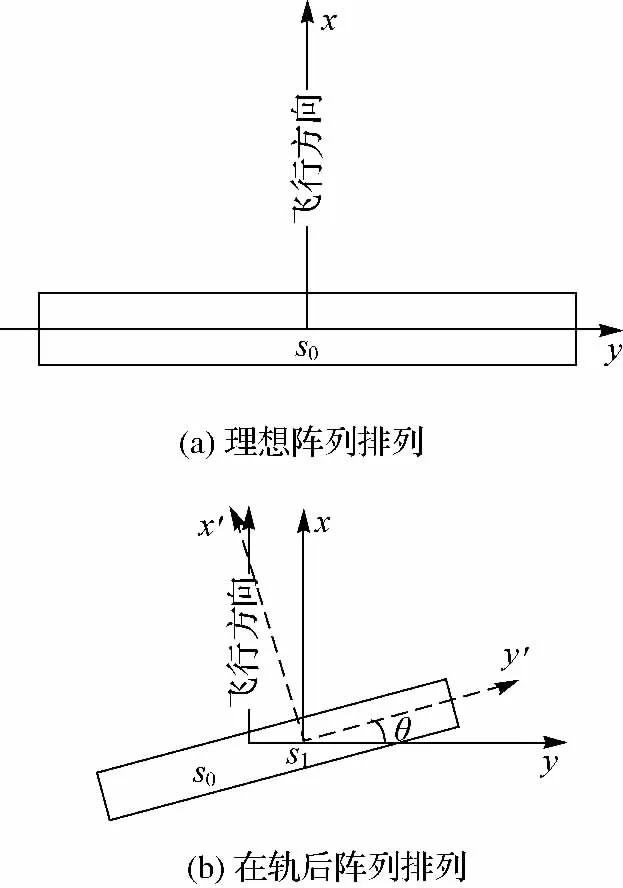
图3 CCD排列旋转误差Fig.3 The rotation angle of CCD line array

如图3（b），现假定线阵列排列旋转角为θ，旋转中心在探元s1位置，而主点位置仍为s0。则对于任意探元s，在坐标系s1x′y′中有

依据图3（b）几何关系，其在s1xy中的坐标为

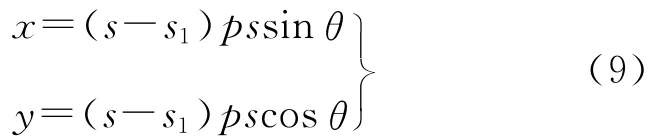
因s1xy与s0xy仅存在坐标平移关系，则s探元的像主点坐标为

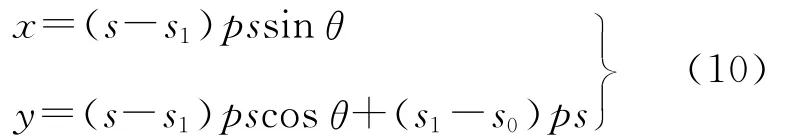
比较式（8）与式（10）可知

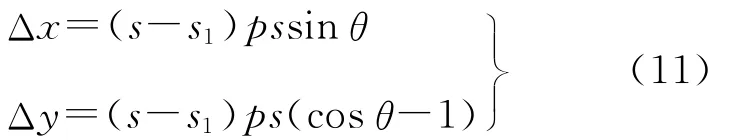
2.2.5 镜头光学畸变

镜头光学畸变主要包括径向畸变及偏心畸变［21－23］。其中径向畸变模型为

偏心畸变模型为

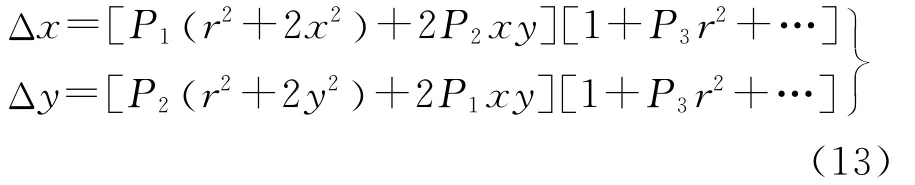
式中，r2＝x2＋y2。

2.2.6 多CCD线阵内方位元素模型

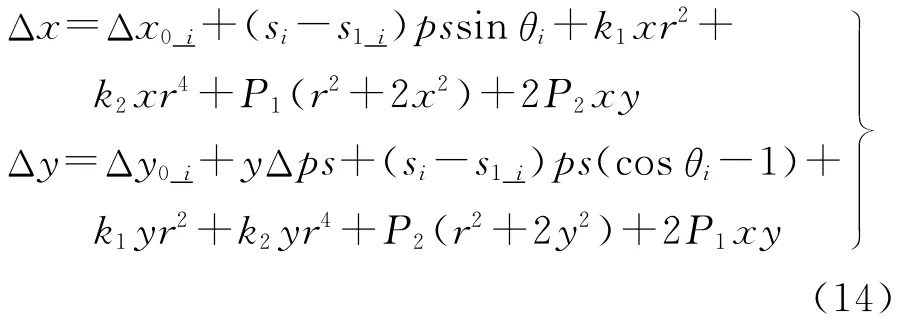
考虑到较短时间内相机内方位元素具有稳定性，因此当利用多检校场进行在轨几何检校时，利用所有影像控制点解求同一套内方位元素模型参数。

3 试验验证及分析

3.1 资源三号测绘卫星几何检校和验证数据

本文利用登封检校场区域和天津范围的1∶2000DOM、DEM作为联合检校的控制数据，其中，登封检校场数据采集于2010年，区域内基本是平原，在西南角存在高差在600m的山地，覆盖范围为50km×50km；天津检校场数据采集于2008年，区域内均为平地，高差小于12m。

联合几何检校中用到的资源三号影像分别为成像于2012－02－03的登封区域三线阵影像及成像于2012－02－28的天津区域三线阵影像。

为了验证偏置矩阵的有效性，选取多个非检校区域资源三号影像与Google Earth上同区域点进行坐标比对来评价偏置矩阵的补偿效果。在试验中，选取Google Earth上几何精度更高的Geoeye、IKONOS图层作为参考。

利用2012－02－18河北安平靶标区域的资源三号三线阵影像验证内方位元素检校的正确性和精确性。该区域覆盖了人工布设的30个靶标控制点，如图4所示，它们的地面坐标由GPS测得，精度优于0.1m；并通过高精度靶标提取算法获取像点坐标，靶标提取精度在0.07～0.1像素，利用该景30个靶标点验证了几何检校后的立体平差精度。

图4 河北安平靶标控制点（▲控制点，● 检查点）Fig.4 The reference points of Anping area（▲control points，●check points）

3.2 偏置矩阵解求试验及分析

3.2.1 偏置矩阵解求

采用高精度相位相关的配准算法［24］对资源三号影像和DOM进行配准，获取高精度控制点。在2012－02－03登封景前、正、后视影像上分别获得4225、33 620、3566个控制点，2012－02－28天津景前、正、后视影像上分别获得1676、2395、1571个控制点。经过误配准点剔除后，各景影像的控制点分布均匀。由于天津区域资源三号影像与天津区域1∶2000的DOM成像间隔较大，地物有变化，配准精度和配准点个数不及2012－02－03登封景。表2为资源三号正视相机偏置矩阵解求后精度评价结果（前后视相机结果一致），为方便比对说明，将内方位元素检校后精度评价结果提前列表。

由表 2可知，2012－02－03登封景、2012－02－28天津景定位精度非常接近。由于卫星发射过程中受力，相机安装矩阵在轨后发生变化，影像的直接定位精度较差，沿轨约为128像素（128像素×2.1m＝268.8m），垂轨向约422像素（422像素×2.1m＝886.2m）。解求两景的偏置矩阵后，其几何定位精度提升明显，沿轨向精度优于1像素，垂轨向优于2像素。

表2 资源三号几何检校精度（正视）Tab.2 Calibration accuracy of ZY－3nadir camera 像素

3.2.2 偏置矩阵补偿精度验证

利用2012－02－03登封景检校获得的偏置矩阵对其他时间和地点获取的资源三号影像进行补偿处理，利用Google Earth高分图层验证了内蒙古、安徽、江西、宁波等区域三线阵影像中正视影像平面精度均优于20m，如表3所示。该结果表明偏置矩阵补偿了资源三号相机安装及姿轨测量的系统误差，提升了资源三号三线阵无控定位精度。

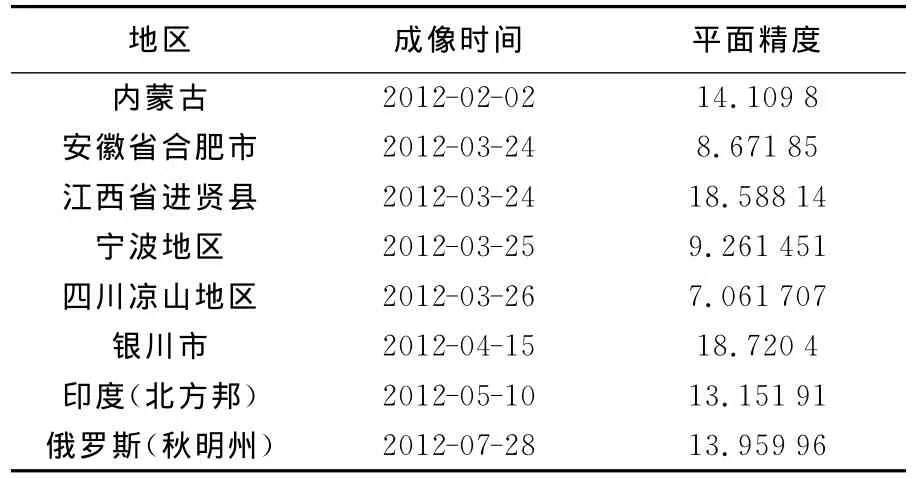
表3 资源三号正视相机偏置矩阵补偿精度Tab.3 Positioning accuracy with offset matrix of ZY－3 nadir camera m

3.3 内方位元素检校试验及分析

3.3.1 内方位元素误差模型参数解求

从表2可知，通过偏置标定后，垂直轨道方向存在接近两个像素的误差。2012－02－03登封景正视影像解求偏置矩阵以后的残差图（前、后视影像规律一致）如图5所示，其中横坐标为影像列，纵坐标为垂轨、沿轨残差。

从图5可看到，垂轨、沿轨误差均呈现较为明显的线性规律，且各片CCD间残差大小略有差异（图中虚线椭圆所示）。资源三号三线阵相机设计为无镜头光学畸变系统，一般镜头畸变均为高阶误差，可推测正视相机镜头畸变非常小。考虑内方位元素线性误差中，比例误差仅影响垂轨向精度，而旋转角误差既影响垂轨向精度，又影响沿轨向精度，且均为线性规律。可推测正视相机中内方位元素误差不存在光学镜头畸变，而仅可能存在主点偏移、比例缩放及CCD排列旋转角误差。因此，本文标定中对资源三号三线阵影像仅解求主点偏移、比例缩放及CCD排列旋转误差。内方位元素检校后的精度评价结果见表2。在式（14）中，由于线阵CCD中x≈0，且一般排列旋转角很小，因此内方位元素误差主要影响垂轨方向，经过内方位元素几何检校后主要提升垂轨向精度。由表2可知，经过内方位元素检校后，沿轨向精度没有明显改善，但垂轨向精度提升明显，且两景均优于0.3像素。但2012－02－28天津景几何检校后精度不及2012－02－03登封景，这是由配准精度差异造成的。

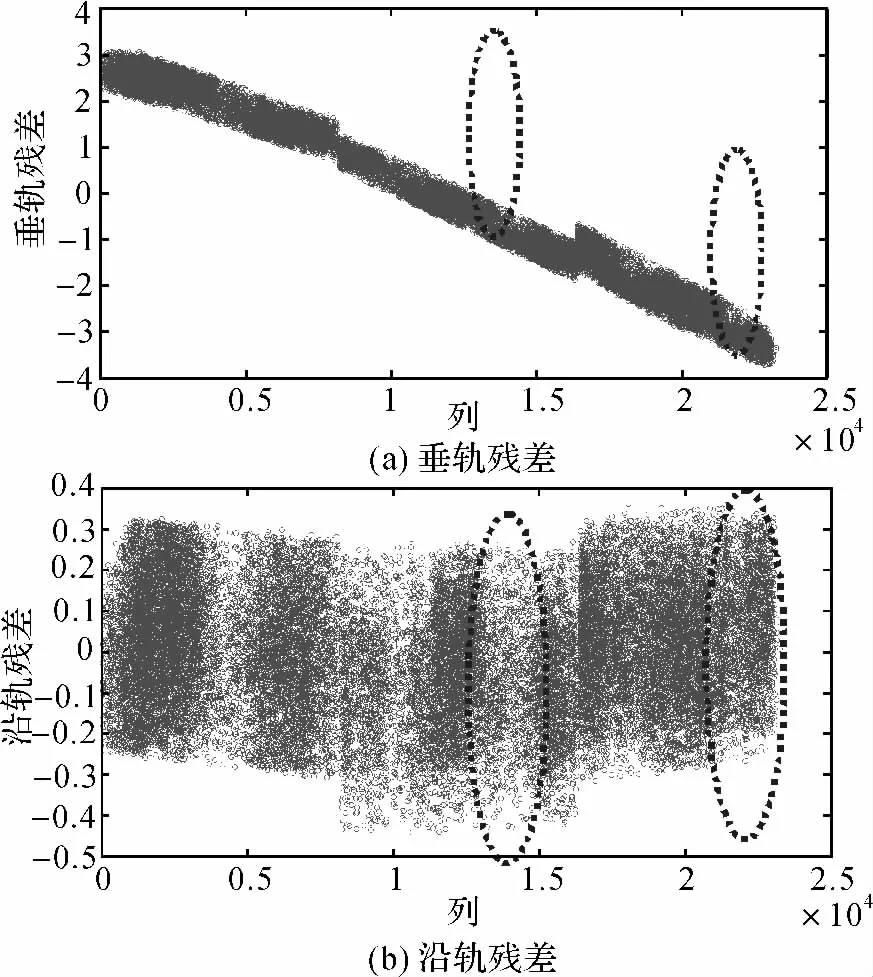
图5 2012－02－03登封景正视影像解求偏置矩阵后残差规律图Fig.5 Residual error feature of 2012－02－03Dengfeng nadir image after calculating the offset matrix

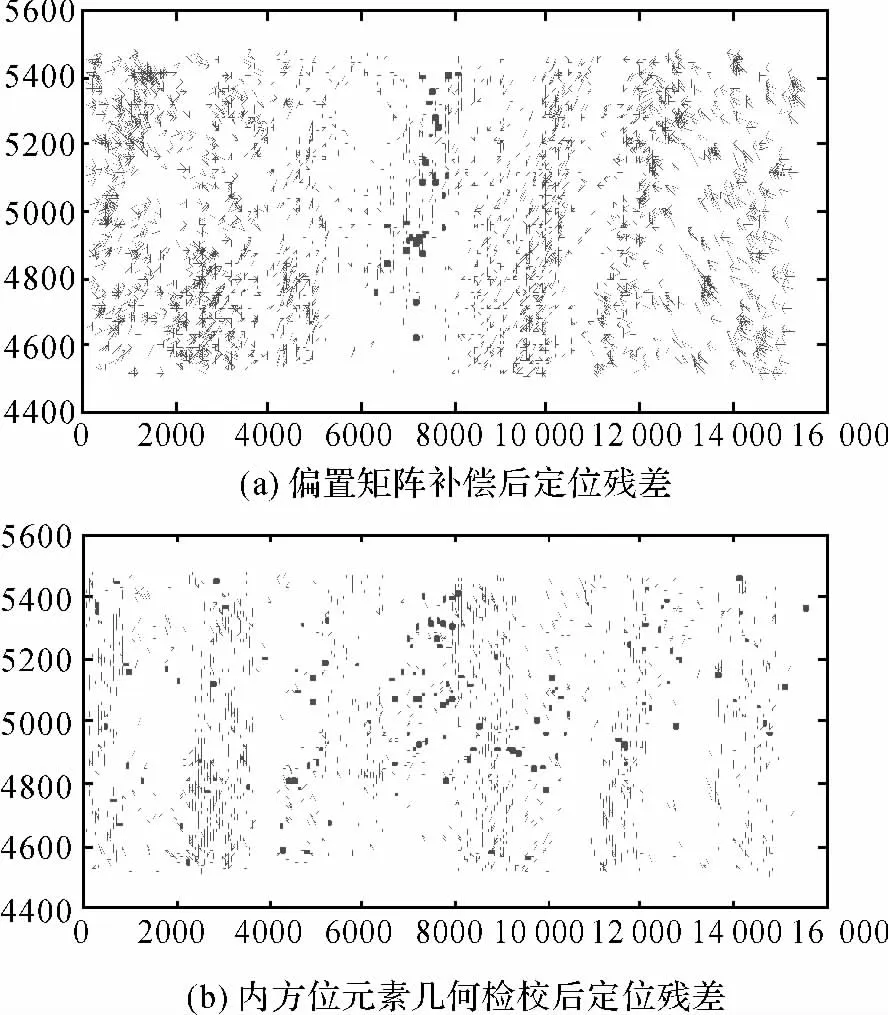
图6 2012－02－03登封景前视影像几何检校残差图Fig.6 Residual error of 2012－02－03Dengfeng foward image after geometric calibration

图6为2012－02－03登封景几何检校后的定位残差图，从图6（a）中可以看到，经过偏置矩阵解求后，定位残差图呈现“两边大、中间小”的趋势，具有一定的对称性；而图6（b）中，进一步经过内方位元素几何检校后，残差不存在明显的畸变特性，分布随机。

3.3.2 内方位元素检校精度验证

在内方位元素检校基础上，利用河北安平区域靶标点验证整个几何检校后的立体平差精度（包含三视和两视情况）。采用高分光学影像中基于RFM模型的像面仿射模型作为立体平差模型，一共设置3组平差条件，平差结果如表4所示：

（1）直接利用安平区域资源三号影像进行平差，30个靶标点均作为检查点。

（2）选取周边6个靶标点作为控制点，其余24个靶标点作为检查点，进行立体平差，控制点分布如图4所示。

（3）将30个靶标点全部作为控制点，进行立体平差。

表4 内方位元素检校后立体平差Tab.4 Block adjustment result after interior calibration m

资源三号测绘卫星设计的立体交会角约为47°，对应基高比约为0.87。靶标提取精度在0.07～0.15像素之间（提取精度与靶标清晰度和信噪比有关），根据摄影测量基高比与高程精度之间关系

在靶标点区域，资源三号理论高程精度在0.40～0.85m之间。由表4，利用多检校场联合几何检校的结果进行带控立体平差中，最大高程误差优于1m，高程中误差优于0.5m，均接近在靶标条件下资源三号所能达到的理论精度，也同时验证了几何检校结果的可靠性。

4 结 论

本文对星载光学的常规严密成像几何模型进行了相关参数合并，构建了用于几何检校的严密成像几何模型，在模型中引入偏置矩阵，消除了由姿轨测量、载荷安装等系统误差对几何定位精度的影响，提升了卫星的无控制点定位精度；推导了多线阵CCD内方位元素模型，消除了相机内部畸变对几何定位精度的影响，提升了卫星影像的内部几何精度；提出了多检校场联合检校的几何模型及检校方案，利用该模型对资源三号三线阵影像进行在轨几何检校。通过对试验结果的分析，可以得出如下结论：① 偏置矩阵能够补偿资源三号测绘卫星在轨成像的载荷安装、姿轨测量等系统误差，从而提高影像的无控定位精度，经过偏置矩阵补偿后，资源三号三线阵影像无控平面精度优于20m；② 建立多线阵CCD拼接的内方位元素模型，在完成在轨内方位元素检校后，资源三号三线阵影像带靶标控制点的平面定位精度优于0.6m，高程精度优于0.5m，达到在靶标点条件下资源三号测绘卫星所能达到的理论极限精度。

［1］ XU Jianyan，HOU Minghui，YU Jin，et al.Study of CBERS CCD Camera Bias Matrix Calculation and Its Application［J］.Spacecraft Recovery and Remote Sensing，2004，25（4）：25－29.（徐建艳，侯明辉，于晋，等.利用偏移矩阵提供CBERS图像预处理几何定位精度的方法研究［J］.航天返回与遥感，2004，25（4）：25－29.）

［2］ YUAN Xiuxiao，YU Xiang.Calibration of Angular Systematic Errors for High Resolution Satellite Imagery［J］.Acta Geodaetica et Cartographica Sinica，2012，41（3）：385－392.（袁修孝，余翔.高分辨率卫星遥感影像姿态角系统误差检校［J］.测绘学报，2012，42（3）：385－392.）

［3］ YUAN Xiuxiao，YU Junpeng.Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery［J］.Acta Geodaetica et Cartographica Sinica，2008，37（1）：36－41.（袁修孝，余俊鹏.高分辨率卫星遥感影像的姿态角常差检校［J］.测绘学报，2008，37（1）：36－41.）

［4］ BECKETT K，RAMPERSAD C，PUTIH R，et al.Rapideye Product Quality Assessment［C］∥ Proceedings of SPIE.Berlin：SPIE，2009：1－10.

［5］ BOUILLON A，BRETON E，DE LUSSY F，et al.SPOT5 HRG and HRS First In－flight Geometric Quality Results［C］∥ Pelagia：［s.n.］，2002：212－223.

［6］ BOUILLON A，BRETON E，DE LUSSY F.SPOT5Geometric Image Quality［C］∥ Proceedings of 2003IEEE International Geoscience and Remote Sensing Symposium.Toulouse：IEEE，2003：303－305.

［7］ TADONO T，SHIMADA M，MURAKAMI H，et al.Initial Results of Calibration and Validation for PRISM and AVNIR－2［J］.Asian Journal Geoinformation，2006，6（4）：11－20.

［8］ DIAL G，GRODECKI J.Ikonos Accuracy without Ground Control［C］∥Proceedings of ISPRS Commission.［S.l.］：ISPRS，2002.

［9］ GRODECKI J，DIAL G.Ikonos Geometric Accuracy Validation［C］∥Proceedings of ISPRS Commission.［S.l.］：ISPRS，2002.

［10］ MULAWA D.On－orbit Geometric Calibration of the Orb－View－3High Resolution Imaging Satellite［J］.International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences，2004，35（B1）：1－6.

［11］ TADONO T，SHIMADA M，HASHIMOTO T，et al.Results of Calibration and Validation of ALOS Optical Sensors，and Their Accuracy Assesments［C］∥ Proceedings of Geoscience and Remote Sensing Symposium.Barcelona：IGARSS，2007.

［12］ TANG Zhiqiang，SU Wenbo，GE Haijun.The Inner Orientation Modeling and Optimization of Space Line－array CCD Sensor［J］.Remote Sensing Information，2010（6）：3－5.（汤志强，苏文博，葛海军.航天线阵CCD传感器内方位建模与优化［J］.遥感信息，2010（6）：3－5.）

［13］ TANG Zhiqiang，FAN Dazhao，LIU Chubin，et al.Inner Orientation Modeling and Validation for Nadir Sensor of ALSO／PRISM［J］.Science of Surveying and Mapping，2011，36（6）：35－36.（汤 志 强，范 大 昭，刘 楚 斌，等.ALSO／PRISM下视传感器内方位分析与建模［J］.测绘科学，2011，36（6）：35－36.）

［14］ ZHANG Guo，LI Deren，YUAN Xiuxiao，et al.The Mapping Accuracy of Satellite Imagery Block Adjustment［J］.Journal of Zhengzhou Institute of Surveying and Mapping，2006，23（4）：239－241.（张过，李德仁，袁修孝，等.卫星遥感影像的区域网平差成图精度［J］.测绘科学技术学报，2006，23（4）：239－241.）

［15］ ZHANG Guo，LI Yang，ZHU Xiaoyong，et al.Application of RFM in Geometric Rectification of Optical Satellite Image［J］.Spacecraft Recovery and Remote Sensing，2010，31（4）：51－57.（张过，李扬，祝小勇，等.有理函数模型在光学卫星影像几何纠正中的应用［J］.航天返回与遥感，2010，31（4）：51－57）

［16］ 卫星测绘应用中心.资源三号高分辨率立体测图卫星大事记［EB／OL］.［2012－02－01］.http：∥www.sasmac.cn／portal＿space／

［17］ LI Deren.China’s First Civilian Three－line－array Stereo Mapping Satellite： ZY－3 ［J］.Acta Geodaetica et Cartographica Sinica，2012，41（3）：317－322（李德仁.我国第一颗民用三线阵立体测图卫星—资源三号卫星［J］.测绘学报，2012.41（3）：317－322）

［18］ TANG Xinming，ZHANG Guo，ZHU Xiaoyong，et al.Triple Linear－array Imaging Geometry Model of ZIYuan－3 Surveying Satellite and Its Validation［J］.Acta Geodaetica et Cartographica Sinica，2012，41（2）：191－198.（唐新明，张过，祝小勇，等.资源三号测绘卫星三线阵成像几何模型构建与精度初步验证［J］.测绘学报，2012，41（2）：191－198）

［19］ ZHANG Guo.Rectification for High Resolution Remote Sensing Image under Lack of Ground Control Points［D］.Wuhan：Wuhan University，2005.（张过.缺少控制点的高分辨率卫星遥感影像几何纠正［D］.武汉：武汉大学，2005.）

［20］ LIU Bin.Space－ground Intergated Attitude Determination of High－resolution Satellite and Geometric Image Processing under Jitter Conditions［D］.Wuhan：Wuhan University，2011.（刘斌.高分辨率光学卫星空地一体化定姿及姿态抖动下影像几何处理方法研究［D］.武汉：武汉大学，2011.）

［21］ BROWN D C.Close－range Camera Calibration［J］.Photogrammetric Engineering and Remote Sensing，1971，37（8）：855－866.

［22］ FRASER C S.Digital Camera Self－calibration［J］.ISPRS Journal of Photogrammetry and Remote Sensing，1997，52（4）：149－159.

［23］ FRYER J G.Lens Distortion for Close－range Photogrammetry［J］.Photogrammetric Engineering and Remote Sensing，1986，52（1）：51－58.

［24］ LEPRINCE S，BARBOT S，AYOUB F，et al.Automatic and Precise Orthorectification，Coregistration，and Subpixel Correlation of Satellite Images，Application to Ground Deformation Measurements［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45（6）：1529－1558.