ClF-分子离子的结构与势能函数

李 松 陈善俊 朱德生 韦建军

(1长江大学物理科学与技术学院,湖北荆州 434023;2四川大学原子与分子物理研究所,成都 610065)

1 引言

分子离子是自然界中广泛存在的物质形态,它们产生并存在于自然界及实验室的等离子体系、化学反应过程、燃烧过程以及星际物质中.双原子分子(包括双原子分子离子)的几何结构和势能变化趋势可以通过其相应的解析势能函数进行描述.1,2由解析势能函数可以进一步对分子的碰撞和反应动力学性质开展研究,并且还为研究多原子分子提供了理论依据.3-5

卤族元素是化学性质非常活泼的非金属元素,由于其电子亲和能较大,所以很容易获取一个电子而形成一价的负离子,并通过各种化学反应形成金属卤化物、卤素互化物、卤代化合物等.其中,碱金属卤化物晶体在光照射的条件下可以由透明的反磁性体成为有色的顺磁物质,后来发现使其着色的是ClF-等卤素互化物分子离子.在此之后,ClF-分子离子成为众多课题组的研究对象.6-13在实验方面,Wilkins和Gabriel6在经X射线照射的处于液氮温度的KCl-KF晶体中发现了ClF-分子离子,并通过电子自旋共振方法研究了(111)ClF-的电子结构.Schoemaker7也通过相同的方法对掺氟碱金属卤化物晶体中的(111)FX-(X=Cl,Br,I)体系进行了实验研究,并与同核卤素双原子分子离子的相关性质进行了比较.Susman8开展了针对ClF-的远红外吸收光谱研究,并指出,当ClF-占据了晶体中的一个格点时,其伸缩振动频率与气态的自由ClF-分子离子相比并没有太大的变化.Griscom和Friebele9在进行实验探测的同时还对电子自旋共振的谱线线型进行了计算机模拟.Delbecq等10在掺有PbCl2和KCl的KF晶体中对(110)ClF-的吸收光谱进行了实验探测,并定性地分析了(111)ClF-和(110)ClF-相关性质的差别.在理论研究方面,Van Huis等11利用BLYP、B3LYP、BHLYP、BP86等几种密度泛函理论方法结合DZP、DZP++基组对ClFn(n=1-7)和相应的一价负离子进行了理论计算,得到了各体系的平衡核间距和离解能.Bruna和Greinr12对ClF-分子离子的电子自旋磁矩进行了研究,并在MP2/6-311+G(2df)理论水平计算了该体系的平衡核间距.Midda和Das13采用B3LYP方法结合系列相关一致基组对ClF-分子离子的平衡结构和光谱常数进行了计算,并将计算结果进行了基组外推.不过,以上理论研究均没有给出该体系的解析势能函数,而该体系各能级的有关分子常数也无从得知.

本文利用从头计算方法QCISD(T)和CCSD(T)结合系列相关一致基组对35ClF-和37ClF-分子离子分别进行了结构优化和单点能扫描计算.其中,对CCSD(T)方法的计算结果进行了基组外推.通过对单点能数据进行最小二乘拟合得到了体系在基态的解析势能函数,并在此基础上计算得到了两种同位素分子离子完整的光谱常数.基于拟合所得解析势能函数,通过求解核运动的径向薛定谔方程得到了转动量子数J=0时35ClF-和37ClF-(X2Σ+)的各振动态.对于每一个振动态还计算得到了相应的惯性转动常数以及离心畸变常数.本文的有关计算结果为进一步的实验和理论研究提供了参考依据.

2 35ClF-和37ClF-分子离子的电子态和离解极限

要准确表达分子体系的势能函数,必须事先确定其正确的离解极限.根据文献12,13中给出的结果,ClF-分子离子的基态是X2Σ+.该结论也被本文结构优化计算的结果所确认.ClF-分子离子为线性双原子分子,属于C∞v群,其离解通道有可能是Cl-+F或者F-+Cl.由于F原子相比Cl原子更容易形成负离子,因此ClF-分子离子的离解极限应为后一种形式.我们的推测通过对ClF-进行Mulliken原子电荷分析得到了证实.当ClF-的核间距大于0.5 nm时,ClF-分子离子已经离解成了F-离子和Cl原子.F-离子的基态为1Sg,Cl原子的基态为2Pu.当二者反应生成ClF-分子离子时,F-和Cl的对称性降低.根据原子分子反应静力学基本原理,14这两个离解产物的原子群分别分解为C∞v分子群的不可约表示,即1Sg(F-)→1Σ+,2Pu(Cl)→2Σ++2Π.ClF-分子离子可能的电子态可以通过二者的直积约化得到:

可以看到结果中含有该体系的基态2Σ+.根据微观过程的可逆性原理,ClF-分子离子在基态的离解极限为

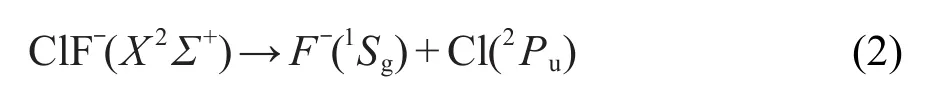
3 理论方法与计算

利用Gaussian 03程序中的单双取代包括三重激发的二次组态相互作用的QCISD(T)方法15和单双取代包括三重激发的耦合簇理论的CCSD(T)方法,16结合 aug-cc-pVXZ(X=D,T,Q,5)基组17-20对35ClF-和37ClF-分子离子进行了结构优化计算.同时,本文还利用相同的方法和基组对ClF中性自由基进行了计算,所得平衡核间距被用来计算35ClF和37ClF体系的绝热电子亲和能(AEA)和垂直电子亲和能(VEA).35ClF-和37ClF-分子离子的垂直解离能(VDE)也同时计算得出.本文在aug-cc-pVXZ(X=D,T,Q,5)基组计算结果的基础上采用了基组外推的方法.虽然选用更大的基组进行计算可以提高计算结果的精度,但是需要占用更多的计算资源.而且基组的不完备性仍然是使计算精度受限的原因.基组外推可以减小基组截断误差给计算结果带来的影响,使其更接近实际值,是得到高精度结果的有效方法.20-23因此,采用基组外推方法兼顾了计算的精度和效率.

针对35ClF-和37ClF-体系的单点能扫描在CCSD(T)理论水平进行.扫描范围为0.15-1.00 nm,扫描步长为0.005 nm,而在平衡核间距附近扫描步长减小为0.002 nm.因此,四种不同基组计算得到的能量数据点各有203个.将这四组数据中对应相同核间距的能量点进行基组外推,可以得到在基组极限的各点能量值.在本文中,基组外推采用四种方法,相应的计算公式分别为20-23

式中E(X)和ECBS分别是计算以及外推所得各单点能能量.X=2,3,4,5分别对应相关一致基组的DZ、TZ、QZ和5Z.各式中的a、b和c分别是拟合系数.由于计算的对象以及所用方法与基组不一样,要确定哪一种外推公式更合适是非常困难的,所以并没有哪一个公式是普适的最佳外推公式.24-26由于公式(3)和公式(5)的外推结果往往略为偏小,而公式(4)和公式(6)的计算结果又有所高估,所以在实际应用中往往将两种或几种外推结果的平均值作为基组极限的数据.24,27因此,本文取上述四种方法的平均值作为最终的外推结果.公式(3)至公式(6)的外推计算结果在本文中分别用CBS1至CBS4表示,四者的平均值用CBS表示.

Murrell-Sorbie(M-S)势能函数28能够很好地表示双原子分子的解析势能函数.该函数也被广泛运用于表示多原子分子体系势能函数多体展开项中的二体项.M-S势能函数可以表示为

其中,De是离解能,ai是拟合参量,ρ=R-Re,R与Re分别是核间距以及平衡核间距.

体系的力常数可以通过对解析势能函数求导得到,由此得到的二阶至四阶力常数可分别表示为29

根据力常数与光谱常数的关系可以进一步通过下列各式求得体系的光谱常数

上述各式中,μ是体系的约化质量,c是真空中的光速,Be与αe分别是刚性转动因子和非刚性转动因子,ωe、ωeχe分别是谐振频率和非谐性常数,Drot是离心畸变常数.

基于结构优化以及单点能扫描的数据,利用Level 8.0程序30通过求解双原子径向核运动的薛定谔方程,计算得到了J=0时35ClF-和37ClF-电子基态的所有振动能级,并进一步对各振动能级的惯性转动常数以及离心畸变常数分别进行了计算.

4 结果与讨论

4.1 基态35ClF-和37ClF-(X2Σ+)的结构参数

本文分别用QCISD(T)和CCSD(T)方法对35ClF-和37ClF-进行了结构优化计算.其中,CCSD(T)方法的计算结果被外推至基组极限.计算所得平衡核间距Re、经零点能修正的体系总能量E和离解能De均列于表1.从表中可以看出,用QCISD(T)和CCSD(T)两种计算方法得到的平衡核间距均在0.215 nm左右,相比其中性分子的平衡核间距Re(ClF)(0.1628 nm)31增大了约25%.在四种外推计算的结果中,数值最大的CBS4(0.21557 nm)和最小的CBS3(0.21483 nm)只相差约0.3%,表明这四种外推方法的结果是非常接近的.而且CBS1与CBS3的计算数据偏小,而CBS2与CBS4的结果稍大.四种外推结果的平均值为0.21523 nm.虽然没有实验结果进行对比,但是本文的计算值与有关文献数据还是很相符的.文献12中采用MP2方法计算得到的平衡核间距为0.2050 nm,比本文基组外推平均值偏小约5%.而文献11,13中采用密度泛函方法的计算结果比本文结果偏大约5%.相对而言,由于文献12中的MP2/6-311+G(2df)方法计算精度有限,而文献11,13中的密度泛函方法考虑电子相关效应不足,所以本文对在较高理论水平采用较大基组的计算结果进行基组外推所得数据应该更为可靠.此外,经零点能校正的离解能De用四种外推方法计算的四个结果也非常接近,平均值为1.499 eV.而文献11和文献13的计算值则偏大约10%和16%.

表1 优化计算的35ClF-和37ClF-(X2Σ+)平衡核间距Re,体系总能量E和离解能DeTable 1 Optimized equilibrium internuclear distanceRe,total energy of the systemEand dissociation energyDeof 35ClF-and37ClF-(X2Σ+)

为了表明本文计算对该研究体系的适用性,我们还利用完全相同的计算方法和外推方法对ClF自由基进行了验证性的计算,并将计算结果与有关文献数据进行比较.对比的结果显示出了很好的一致性(具体见后文4.3节部分).因此,本文所采用的计算方法是可靠的,计算所得数据是可信的.

4.2 基态35ClF-和37ClF-(X2Σ+)的解析势能函数和光谱常数

对CCSD(T)/aug-cc-pVXZ(X=D,T,Q,5)的单点能扫描结果分别用四种方法进行外推并取平均值.用公式(7)所表示的M-S势能函数对计算以及外推的数据分别进行最小二乘拟合.对于其中的拟合参量,截断至高次项可以提高拟合的精度.32本文尝试了n=3至n=9的各种方法,并最终选取n=9拟合各组单点能数据.结果如图1(a)所示,其中的离散点是扫描计算以及基组外推的单点势能值,实线是分别对其进行拟合的结果.图1(b)显示的是势能曲线在平衡核间距附近的细节情况.从图中可见,各组的拟合曲线与相应的各数据点可以很好的吻合.势能曲线的变化趋势呈现出了稳定态的特征.当核间距大于0.5 nm时,势能曲线已经明显趋于离解极限.因此,当前分子离子体系的基态势能函数可以很好地用M-S势能函数表示.拟合的势能函数参量列于表2中.

拟合的均方根误差ERMS可以用来评估拟合的质量,可以表示为33

其中Vcalc和Vfit分别是计算以及拟合的单点能能量值,N是计算的数据点数量(本文取值N=203).在表2中,不同基组计算结果的拟合均方根误差也同时列出.如表中所示,各组单点能计算结果的拟合精度均远小于化学精度(不大于349.75 cm-1).这不仅表明M-S势能函数非常适合于拟合当前体系的势能曲线,而且证明本文的拟合具有很高的精度,其结果是可信的.在拟合结果中,对应不同核间距的单点能数据点的绝对拟合误差可以用图2表示.尽管图中显示个别数据点的拟合误差较大,但是误差与该点的能量数值相比还是很小的.

图1 CCSD(T)方法计算的基态35ClF-和37ClF-(X2Σ+)势能曲线Fig.1 Potential energy curves of the ground states of35ClF-and37ClF-(X2Σ+)calculated by CCSD(T)method

表2 基态35ClF-和37ClF-(X2Σ+)的Murrell-Sorbie势能函数拟合参量Table 2 Parameters of Murrell-Sorbie potential energy function for the ground states of35ClF-and37ClF-(X2Σ+)

在得到M-S势能函数的拟合参量之后,利用公式(8)至公式(10)可以计算得到体系的力常数,其结果列于表3中.可以看出,随着基组的增大,各力常数均呈现出明显的收敛性.根据公式(11)至公式(15)计算得到的35ClF-和37ClF-光谱常数在表4中列出.虽然只有文献13给出了部分光谱常数,但是受限于该文所采用的密度泛函计算方法对电子相关效应考虑不足,各常数的精度不及本文的计算结果,并且其数值均比本文结果偏小.以刚性转动因子Be为例,本文对两种同位素分子离子的外推计算结果分别为0.2956和0.2900 cm-1,而文献13的相应数值则偏小约11%.尽管没有相应的实验数据加以对比,还是有理由相信本文通过高水平计算方法结合基组外推的计算结果更加精确.

图2 势能曲线的拟合误差Fig.2 Fitting errors of potential energy curves

表3 基态35ClF-和37ClF-(X2Σ+)的力常数Table 3 Force constants for the ground states of35ClF-and37ClF-(X2Σ+)

35ClF-和37ClF-两种同位素分子离子谐振频率ωe的基组外推平均值分别为377.2和373.6 cm-1,相比其中性分子的谐振频率(784.1 cm-1)31均减小了约52%,表明当ClF得到一个电子形成负离子之后两原子间的键强有较大幅度的减弱.虽然只有文献13给出了ωe的计算结果,但是其数值比本文结果偏小约24%.对于非刚性转动因子αe和非谐性常数ωeχe,由于aug-cc-pVXZ(X=D,T,Q,5)基组的计算结果并不满足一致收敛性,因此没有进行基组外推.而文献13中这两个常数的结果相比本文aug-cc-pV5Z基组的计算数据明显偏小.

4.3 35ClF和37ClF(X1Σ+)的电子亲和能以及35ClF-和37ClF－(X2Σ+)的垂直解离能

绝热电子亲和能是中性分子与相应的负分子离子处于各自平衡核间距的能量差.垂直电子亲和能则是中性分子和负分子离子均处于中性分子平衡核间距时的能量差.负分子离子的垂直解离能可以表示为中性分子和负分子离子均处于负分子离子平衡核间距时的能量差.尽管Van Huis等11利用密度泛函理论方法与Chen等34在CCSD(T)理论水平已经分别对ClF中性自由基进行了理论计算,考虑到计算的一致性,本文还是对ClF用CCSD(T)/aug-cc-pVXZ(X=D,T,Q,5)方法进行了计算,并将计算结果进行了基组外推,如表5所示.从表中数据的对比可以看出,本文结果与实验及理论计算数据十分吻合.例如,本文通过计算然后进行外推所得ClF中性自由基的平衡核间距为0.16294 nm,与文献30的实验值0.1628 nm仅相差约0.1%.对谐振频率的比较也有类似的结果.本文的外推计算数据为789.73 cm-1,与实验值31,35非常吻合.以上对比表明本文计算的ClF结果有较高的精度.这同时也在一定程度上证明了本文计算得到的ClF－分子离子的结果同样具有较高的可信度.

表4 基态35ClF-和37ClF-(X2Σ+)的光谱常数(单位:cm-1)Table 4 Spectroscopic constants for the ground states of35ClF-and37ClF-(X2Σ+)(in cm-1)

表5 CCSD(T)方法计算的基态ClF自由基(X1Σ+)平衡常数Table 5 Equilibrium parameters for the ground state of ClF(X1Σ+)radical with CCSD(T)method

基于本文计算所得ClF中性自由基以及ClF-分子离子的平衡核间距,在CCSD(T)/aug-cc-pVXZ(X=D,T,Q,5)水平上分别计算了中性自由基的电子亲和能与负离子的垂直解离能.所得计算结果列于表6.由于四种基组的计算结果没有表现出明显的一致收敛性,并且aug-cc-pVDZ基组的计算结果相比另外三种基组的结果偏离较大,所以没有采用外推方法.本文利用aug-cc-pV5Z基组计算所得35ClF自由基的AEA和VEA分别为2.248和0.486 eV,35ClF-分子离子的VDE为3.699 eV.而含有同位素37Cl的体系的AEA、VEA和VDE分别为2.223、0.437和3.723 eV.由于ClF中性自由基在形成负分子离子之后,其平衡核间距有约25%的增加,所以计算所得AEA、VEA和VDE的结果相差较大.此外,因为AEA、VEA和VDE均为正值,表明ClF-分子离子比ClF自由基具有更强的热力学稳定性.VEA较大,说明ClF获得电子的能力越强.VDE较大,表明ClF-电离出电子所需要的能量越多.AEA为正值,表明当ClF获得一个电子形成负分子离子之后,电子不会发生自解离.

表6 35ClF和37ClF(X1Σ+)的绝热电子亲和能(AEA)、垂直电子亲和能(VEA)与35ClF-和37ClF-(X2Σ+)的垂直解离能(VDE)Table 6 Adiabatic electron affinity(AEA)and vertical electron affinity(VEA)of35ClF and37ClF(X1Σ+),and vertical detachment energy(VDE)of35ClF-and 37ClF-(X2Σ+)

4.4 基态35ClF-和37ClF-(X2Σ+)的振动能级和分子常数

对基态35ClF-和37ClF-振动能级和分子常数的计算是通过Level 8.0程序进行的.基于结构优化计算所得体系的平衡核间距、离解能,结合势能曲线扫描计算所得各单点能,通过求解核运动的径向薛定谔方程计算了当转动量子数J=0时两个同位素体系电子基态的振动能级.计算过程中,在核间距位于0.15-1.00 nm区间内使用三次样条插值方法进行内插计算,而在核间距小于0.155 nm以及大于0.995 nm时分别用指数函数以及幂函数进行外推.最终得到了这两种同位素分子离子在电子基态的所有振动能级.在此基础上进一步计算了各振动能级的惯性转动常数以及各阶离心畸变常数.计算结果列于表7.由于篇幅所限,表中只列出了两种同位素的各前20个振动能级G(v)以及每一个能级所对应的转动常数Bv、四阶离心畸变常数Dv和六阶离心畸变常数Hv,而略去了较高振动量子数的振动能级以及高阶离心畸变常数Lv、Mv、Nv、Ov.由于目前还没有涉及该体系振动能级的报道,所以本文所得振动能级以及各能级的分子常数有助于对该体系进行同位素识别,以及分别对两种同位素分子离子开展进一步的实验研究,并为在天文观测中发现和识别源于该体系的光谱提供了参考数据.

表7 35ClF-和37ClF-(X2Σ+)的振动能级和惯性分子常数(J=0)(单位:cm-1)Table 7 Vibrational levels and molecular constants for 35ClF-and37ClF-(X2Σ+)withJ=0(in cm-1)

5 结论

采用高水平的从头算计算方法QCISD(T)和CCSD(T)结合系列相关一致基组aug-cc-pVXZ(X=D,T,Q,5)对35ClF-和37ClF-分子离子进行了结构优化和单点能计算,并将其中CCSD(T)方法的计算结果利用四种方法外推至基组极限.计算所得各单点能能量值用Murrell-Sorbie势能函数进行最小二乘拟合,得到了体系的势能曲线.拟合得到的解析势能函数表达式可以准确地描述该体系的几何结构特征以及势能相互作用的变化趋势.在拟合所得各参量的基础上进一步计算了体系的力常数与光谱常数.采用与计算ClF-分子离子完全相同的理论方法对ClF自由基进行了验证性计算.计算结果与实验值的良好一致性证明了本文所用方法的适用性以及所得结果的可靠性.根据结构优化计算所得ClF-与ClF的平衡常数,还计算了35ClF和37ClF自由基的电子亲和能以及35ClF-和37ClF-分子离子的垂直解离能.通过求解核运动的径向薛定谔方程得到了J=0时两种同位素负分子离子体系的振动能级.对于每一个振动态计算得到了相应的惯性转动常数以及离心畸变常数.本文的计算结果为进一步的实验和理论研究提供了理论基础,如解析势能函数可以用于表述相关多原子分子体系势能函数多体展开式中的二体项,光谱常数可以用于预测该体系的谱线强度、谱线分布等光谱特征.

(1)Chen,H.J.;Tang,H.Y.;Cheng,X.L.;Wang,Q.W.Acta Phys.-Chim.Sin.2010,26,740.[陈恒杰,唐海燕,程新路,王全武.物理化学学报,2010,26,740.]doi:10.3866/PKU.WHXB20100240

(2)Wang,R.;Jiang,G.;Meng,D.Q.;Zhu,Z.H.Acta Phys.-Chim.Sin.2009,25,1103.[王 蓉,蒋 刚,蒙大桥,朱正和.物理化学学报,2009,25,1103.]doi:10.3866/PKU.WHXB20090617

(3)Xu,Y.Q.;Gao,X.M.;Zhang,W.J.Acta Phys.-Chim.Sin.2007,23,1075.[许永强,高晓明,张为俊.物理化学学报,2007,23,1075.]doi:10.3866/PKU.WHXB20070721

(4) Zhang,Y.G.;Gao,T.;Li,G.X.;Zhang,C.Y.;Chen,D.;Zhu,Z.H.Acta Phys.-Chim.Sin.2006,22,780.[张云光,高 涛,李桂霞,张传瑜,陈 东,朱正和.物理化学学报,2006,22,780.]doi:10.3866/PKU.WHXB20060703

(5) Li,S.;Han,L.B.;Zhou,Z.L.Density Functional Study of Potential Energy Function of Sulfur Monoxide.Proceedings of 2012 International Conference on Computer Science and Mathematics,Physical Education and Management,Wuahn,Chian,Sept.20-21,2012;Zou,T.R.,Han,H.Y.,Eds.;IEEE Press:Beijing,China,2012.

(6) Wilkins,J.W.;Gabriel,J.R.Phys.Rev.1963,132,1950.doi:10.1103/PhysRev.132.1950

(7) Schoemaker,D.Phys.Rev.1966,149,693.doi:10.1103/PhysRev.149.693

(8) Susman,S.Phys.Stat.Sol.B1970,37,561.

(9) Griscom,D.L.;Friebele,E.J.Phys.Rev.B1991,43,7427.doi:10.1103/PhysRevB.43.7427

(10) Delbecq,C.J.;Hutchinson,E.;Yuster,P.H.J.Chem.Phys.1983,79,1408.doi:10.1063/1.445900

(11) Van Huis,T.J.;Galbraith,J.M.;Schaefer,H.F.,III.Mol.Phys.1996,89,607.

(12) Bruna.P.J.;Greinr,F.Chem.Phys.Lett.2000,318,263.doi:10.1016/S0009-2614(00)00022-1

(13) Midda,S.;Das,A.K.J.Mol.Struct.-Theochem2005,713,101.doi:10.1016/j.theochem.2004.09.047

(14) Zhu,Z.H.Atomic and Molecular Reaction Statics;Science Press:Beijing,1996.[朱正和.原子分子反应静力学.北京:科学出版社,1996.]

(15)Pople,J.A.;Head-Gordon,M.;Raghavachari,K.J.Chem.Phys.1987,87,5968.doi:10.1063/1.453520

(16) Raghavachari,K.;Trucks,G.W.;Pople,J.A.;Head-Gordon,M.Chem.Phys.Lett.1989,157,479.

(17) Dunning,T.H.,Jr.J.Chem.Phys.1989,90,1007.doi:10.1063/1.456153

(18) Kendall,R.A.;Dunning,T.H.,Jr.;Harrison,R.J.J.Chem.Phys.1992,96,6796.doi:10.1063/1.462569

(19)Woon,D.E.;Dunning,T.H.,Jr.J.Chem.Phys.1993,98,1358.doi:10.1063/1.464303

(20) Peterson,K.A.;Woon,D.E.;Dunning,T.H.,Jr.J.Chem.Phys.1994,100,7410.doi:10.1063/1.466884

(21)Helgaker,T.;Klopper,W.;Koch,H.;Noga,J.J.Chem.Phys.1997,106,9639.doi:10.1063/1.473863

(22) Feller,D.J.Chem.Phys.1992,96,6104.

(23) Martin,J.M.L.Chem.Phys.Lett.1996,259,669.doi:10.1016/0009-2614(96)00898-6

(24)Dixon,D.A.;de Jong,W.A.;Peterson,K.A.;McMahon,T.B.J.Phys.Chem.A2005,109,4073.doi:10.1021/jp044561e

(25) Feller,D.;Peterson,K.A.;Crawford,T.D.J.Chem.Phys.2006,124,054107.doi:10.1063/1.2137323

(26) Feller,D.;Peterson,K.A.J.Chem.Phys.2007,126,114105.doi:10.1063/1.2464112

(27) Balabanov,N.B.;Peterson,K.A.J.Phys.Chem.A2003,107,7465.doi:10.1021/jp035547p

(28) Murrell,J.N.;Sorbie,K.S.J.Chem.Soc.Faraday Trans.21974,70,1552.doi:10.1039/f29747001552

(29) Zhu,Z.H.;Yu,H.G.Molecular Structure and Molecular Potential Energy Function;Science Press:Beijing,1997.[朱正和,俞华根.分子结构与分子势能函数.北京:科学出版社,1997.]

(30) Le Roy,R.J.Level 8.0:AComputer Program for Solving the Radial Schrdinger Equation for Bound and Quasibound Levels,University of Waterloo Chemical Physics Research Report CP-663;see http://leroy.uwaterloo.ca/programs.

(31) Huber,K.P.;Herzberg,G.Molecular Spectra and Molecular Structure.IV.Constants of Diatomic Molecules;Van Nostrand Reinhold Company:New York,1979.

(32)Wang,X.Q.;Yang,C.L.;Su,T.;Wang,M.S.Acta Phys.Sin.2009,58,6873.[王新强,杨传路,苏 涛,王美山.物理学报,2009,58,6873.]

(33) Shi,D.H.;Zhang,J.P.;Sun,J.F.;Liu,Y.F.;Zhu,Z.L.Acta Phys.Sin.2009,58,5329.[施德恒,张金平,孙金锋,刘玉芳,朱遵略.物理学报,2009,58,5329.]

(34)Chen,L.;Woon,D.E.;Dunning,T.H.,Jr.J.Phys.Chem.A2009,113,12645.doi:10.1021/jp905064v

(35) Bürger,H.;Schulz,P.;Jacob,E.;Fähnle,M.Z.Naturforsch.Teil A1986,41A,1015.