课本不等式应用三重境界

☉浙江省嘉兴市第一中学 王剑明

近几年来，一个重要的不等式每年都出现在高考试题中，像一个幽灵，盘旋在高考的上空.利用这个重要的不等式，可轻松破解2013年新课标全国卷Ⅱ的压轴大题.高考命题者的再次厚爱，可谓情有独钟，让我们再次思考高考命题者的用意，感受它不平凡的价值.

课本不等式：证明不等式ex＞1+x，x≠0.

来源：人教版数学选修2－2第一章导数应用第32页习题1.3B组第1（3）题.

证明：令f（x）=ex－1－x，则f′（x）=ex－1，从而当x＞0时，f′（x）＞0，f（x）单调递增；当x＜0时，f′（x）＜0，f（x）单调递减.

故f（x）的极小值为f（0）=0，即f（x）=ex－1－x≥0，等号当且仅当x=0时取到.

所以不等式ex＞1+x，x≠0得证.

利用该结论易得：结论1：若x∈R，则ex≥1+x，当且仅当x=0时等号成立.结论2：若x＞－1，则ln（1+x）≤x，当且仅当x=0时等号成立.

背景：高等数学中有一个常见而重要的结论——泰勒（Taylor）公式：

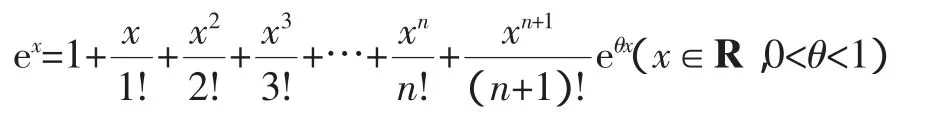
历年高考都把对导数的考查作为提高试题区分度的重要手段，而课本不等式ex≥1+x在导数中发挥着重要的作用.本文将以高考题为例对课本不等式ex≥1+x进行三层运用，从层层深入的角度来达到运用课本不等式ex≥1+x的三重境界.

一、变式求证——不识庐山真面目，只缘身在此山中

在高考中，命题者变换形式，给它披上一件马甲，初看不是这个课本不等式，实际上只要等价变换一下就是这个课本不等式.它的用意就是要求我们重视课本，即使以前高考考过，只要是经典仍就可以考.当然这是浅层次的考法，给考生一个信心和人文关怀.这一类问题的后续问题往往较为困难.

（2）若f（x）≥g（x）恒成立，求实数a的取值范围.

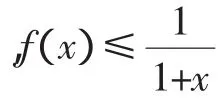
令h（x）=f（x）－（1－x），x∈［0，1］，则h（x）=（1+x）e－2x－（1－x），h′（x）=（－1－2x）e－2x+1.

h″（x）=（2x+2）e－2x＞0，从而h′（x）在x∈［0，1］上递增，故h′（x）≥h′（0）=0，所以h（x）在x∈［0，1］上递增，h（x）≥h（0）=0，即f（x）≥1－x.

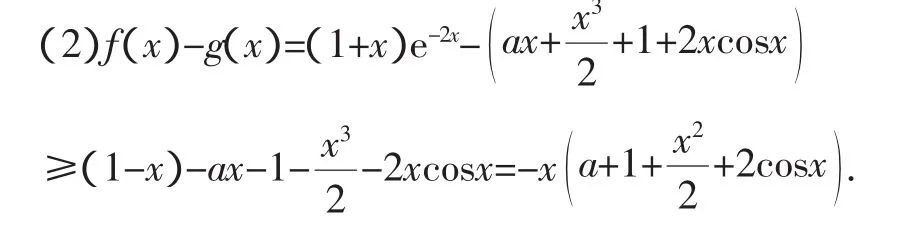
记H（x）=x－2sinx，则H′（x）=1－2cosx.

当x∈（0，1）时，H′（x）＜0，于是H（x）在［0，1］上是减函数，从而当x∈（0，1）时H（x）＜H（0）=0，所以G（x）在［0，1］上是减函数，于是G（x）≤G（0）=2.

从而a+1+G（x）≤a+3，所以当a≤－3时，f（x）≥g（x）恒成立.

因为当x∈（0，1）时，I′（x）＜0，故I（x）在［0，1］上是减函数，于是I（x）在［0，1］上的值域为［a+1+2cos1，a+3］

所以当a＞－3时，存在x0∈（0，1），使得I（x0）＞0，此时，f（x0）＜g（x0），不符合，所以实数a的取值范围是（－∞，－3］.

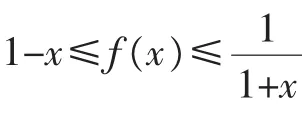
二、暗示给出——无可奈何花落去，似曾相识燕归来

在高考中，命题者更多的是暗示给出这个课本不等式，但往往很多学生没有意识到这个重要的课本不等式，乃至无法下手，颇有一种似曾相识的感觉.往往是求一个函数的最大值或最小值，或求一个不等式恒成立时参数的范围，或求函数的单调区间等命题技巧来让考生领悟到这个课本不等式.当然这是较高层次的考法，给考生一个梯子，考查考生获取新知识的能力和灵活运用新知识的能力.

例2 （2010年新课标全国高考理科数学试题）设函数f（x）=ex－1－x－ax2.

（1）若a=0，求f（x）的单调区间；

（2）若当x≥0时f（x）≥0，求a的取值范围.

解析：（1）a=0时，易得f（x）的单调递减区间为（－∞，0），单调递增区间（0，+∞）.

（2）f′（x）=ex－1－2ax.

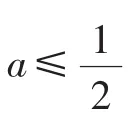
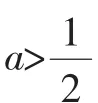
f′（x）＜ex－1+2a（e－x－1）=e－x（ex－1）（ex－2a），

故当x∈（0，ln2a）时，f′（x）＜0，而f（0）=0，于是当x∈（0，ln2a）时，f（x）＜0.

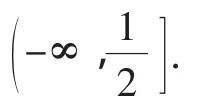
点评：本题主要考查利用导数研究函数性质、不等式恒成立问题以及参数取值范围问题，考查分类讨论、转化与划归解题思想及其相应的运算能力.通过求函数f（x）的单调区间，暗示出重要不等式ex≥1+x，要求恰当利用ex≥1+x，还要巧妙转化为e－x＞1－x（x≠0），并利用它进行放缩，对能力的要求提高了一个层次.不仅要求学习新知识，还要求考生灵活应用新知识.对考生能力要求很高.笔者认为，如果降低技巧性，增强解法的通用性，这种类型的题目可以利用二阶导数的本质而采用一阶导数的形式（从形式上看不超纲），可能会好一点.第（2）小题可以这样解：

因为f′（x）=ex－1－2ax，且f′（0）=0，

所以令g（x）=f′（x），则g′（x）=ex－2a.

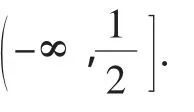
利用二阶导数的本质而采用一阶导数的形式，很多中学数学杂志的论文中也多次使用这个方法，为什么今年新课标全国卷避开这个技巧性较弱的方法，而想出了一些技巧性较强的方法作为标准答案，值得一线数学教师思考.

三、跨度联想——不畏浮云遮望眼，只缘身在最高层

在高考中，涉及到ex，能联想到课本不等式ex≥1+x；涉及到lnx，能联想到课本不等式的变式ln（1+x）≤x，需要扎实的基本功和跨度的联想能力.没有这个课本不等式的地方，看出潜伏下的课本不等式或变式，我以为这就是公式运用的最高境界了.

例3 （2013年新课标全国卷Ⅱ理科数学试题）已知函数f（x）=ex－ln（x+m）.

（1）设x=0是f（x）的极值点，求m，并讨论f（x）的单调性；

（2）当m≤2时，证明f（x）＞0.

由x=0是f（x）的极值点知f′（0）=0，所以m=1.

因此，当x∈（－1，0）时，f′（x）＜0，当x∈（0，+∞）时，f′（x）＞0，所以f（x）在（－1，0）上单调递减，在（0，+∞）上单调递增.

（2）当m≤2，x∈（－m，+∞）时，ln（x+m）≤ln（x+2），

故只需证明当m=2时，f（x）＞0.

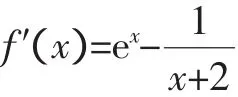
当x∈（－1，x0）时，f′（x）＜0，当x∈（x0，+∞）时，f′（x）＞0，从而当x=x0时，f（x）取最小值.

综上，当m≤2时，f（x）＞0.

点评：本题第（2）问是一个不等式的证明，证明的关键是转化，双变量转化为单变量，然而不难证明.如果跨度联想到课本不等式ex≥x+1以及x≥ln（x+1），则轻松破解.

由ex≥x+1当且仅当x=0时等号成立；ln（x+m）≤x+m－1，当且仅当x=1－m时等号成立，则当m＜2时，x+m－1＜x+1，从而有ex＞ln（x+m）；当m=2时，1－m=－1≠0，从而ex≥x+1与ln（x+m）≤x+m－1两式的等号不能同时成立，从而ex＞ln（x+m）.

所以ex－ln（x+m）＞0，即f（x）＞0.

至此，我们通过课本不等式的三层运用，体验了三重境界，感受了高考命题者的智慧，领悟到了：

（1）课本的重要.课本是老师上课之本，是学生学习之本，更是高考命题之本!高中数学课本是经过资深专家们深思熟虑、千锤百炼而成，汲取了几十年课程改革的经验.课本中的概念、性质、公式、定理、例题、习题、解题思路、阅读材料乃至每章节的文字表述等，具有很强的针对性和逻辑性，蕴含着无数的方法和技巧，并经过无数的教学实践和多年的高考实践的证明，所以千万要以本为本，不能舍本逐末.重视课本习题潜在功能的挖掘和利用，不仅要弄懂课本提供的知识和方法，还要弄清定理、公式的推导过程和例题的求解过程，揭示例、习题之间的联系及变换.

（2）思想的重要.数学思想方法是数学知识的精髓，是知识转化为能力的桥梁，近年的高考试题，十分重视数学思想方法的考查，而课本例习题一般都具有典型性、示范性和迁移性，它们或是渗透了某些数学方法，或体现了某些数学思想，或提供了某些重要结论，因此应充分认识例习题本身所蕴含的价值，掌握其中的通性通法.从这些高考题可以看到，函数的思想、化归的思想用得炉火纯青.只有平时教学中重视思想的渗透，才能让学生在高考选拔中脱颖而出.

（3）变式的重要.这些高考题都是从课本不等式引申、拓展而来，重视变式的训练不仅可以提高学生的数学解题能力，发展不拘一格的意识，而且通过变式来透过表象看清本质，一举切中要害，更重要的是，还可以使学生的逻辑思维水平与形象思维水平得到真正的提高，而这也是新课标体系所要求的.■