左右逢“圆”,四招化险
☉
圆是高中数学的重点内容之一,也是高考命题的热点,高考中我们经常会遇到圆的问题,可以说是左右逢“圆”,如何能够突破圆的包围,出奇制胜?现结合有关圆的题目,用四招轻松化险.
一、识圆

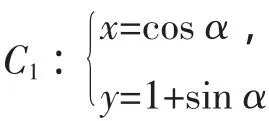
例2 (2011年江西卷)若曲线的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x轴正半轴建立直角坐标系,则该曲线的直角坐标方程为______.
解析:由方程ρ=2sin θ+4cos θ可得ρ2=2ρsin θ+4ρcos θ,由极坐标与直角坐标的转化公式易得x2+y2=2x+4y,即x2+y2-4x-2y=0.
点评:相见却又不能相识,是解题者的一大悲叹,也是考试丢分的主要原因!以上两例是左右逢“圆”的开始,也是解题正确的关键.只有充分的认识圆,不管它以何种方式(参数方程、极坐标等)出现,我们都要能慧眼识珠,这样才能在解题中立于不败之地.
二、用圆
例3 (2011年北京卷)如图1,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②AF·AG=AD·AE;③△AFB∽△ADG,
其中正确结论的序号是( )

图1
A.①② B.②③
C.①③ D.①②③
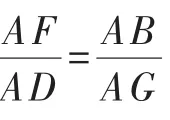
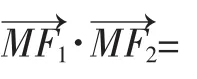
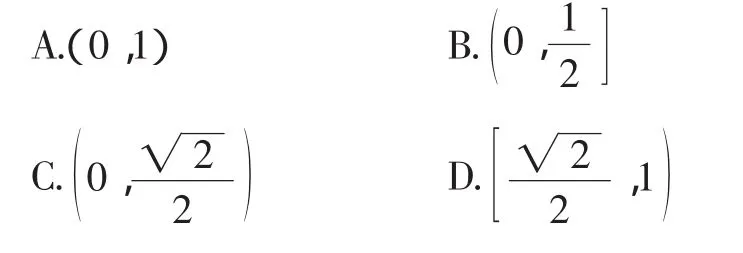


点评:例3中圆的性质运用比较明显,例4的解决应先认识到点M在以椭圆焦距为直径的圆上,又圆周上任意一点都在椭圆内部,则由圆的性质知短半轴长b比圆的半径c大,从而转化为与离心率有关的不等关系.
三、构圆



问题转化为:在三角形AOB的外接圆上求一点C,使得OC最大或者求三角形ABC外接圆的直径.
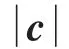
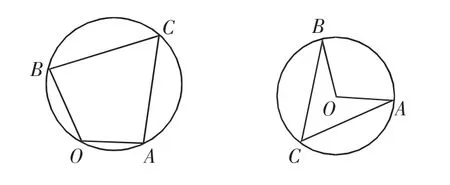
图2


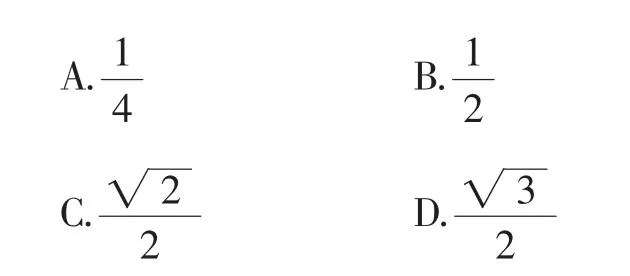
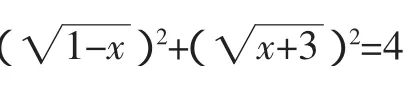

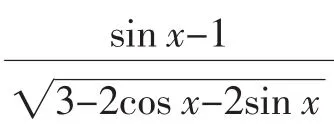

分析:按常规思路思考,比较困难,不妨改变一下思路,从数形结合入手,可通过构造圆来解决问题.


综上所述,所求函数的值域为[-1,0],应选B.
点评:根据题目特征构造圆,将原问题巧妙转化为与圆有关的问题,然后利用圆的有关知识最终将问题顺利解决.此法突破常规,不仅解决了问题,而且发散了同学们的思维,加强了知识间的纵横联系.可谓一举两得,一箭双雕.
四、共圆
例8 (2011年全国新课标卷)如图3,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
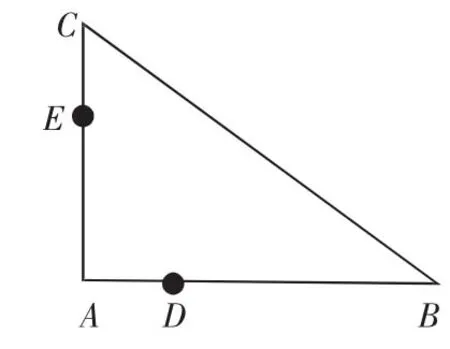
图3
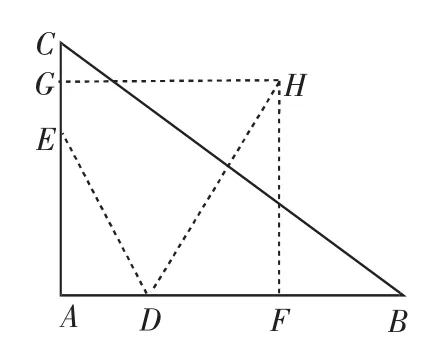
图4
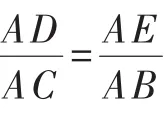
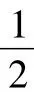
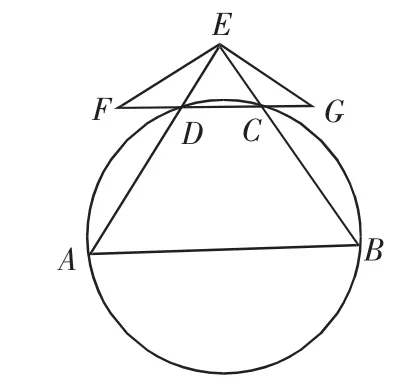
图5
故C,B,D,E四点所在圆的半径为5.
例9(2011年辽宁卷)如图5,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
证明:(1)因为EC=ED,所以∠EDC=∠ECD.因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.故∠ECD=∠EBA,所以CD∥AB.
(2)由(1)知,AE=BE,又因为EF=FG,故∠EFD=∠EGC,从而∠FED=∠GEC.连结AF,BG,则△EFA≌△EGB,故∠FAE=∠GBE,又CD∥AB,∠EDC=∠ECD,所以∠FAB=∠GBA.所以∠AFG+∠GBA=180°,故A,B,G,F四点共圆.
点评:共圆问题在近几年的高考中悄然兴起,成为高考中的一支新军,但却并未引起足够的重视,丢分现象非常严重.以上两例旨在抛砖引玉,以期引起同学们的关注,争取在这方面少丢分,甚至不丢分.

