中考数学压轴题的结构分类评析
☉江苏省泗阳县实验初级中学 朱宜新
中考数学压轴题,涉及知识点多,解答过程运用多种数学思想方法,具有一定的综合性、选拔性.这种题型多采用“组合型”的结构形式,搞清“组合型”压轴题中总条件与分题间及分题与分题间的结构关系,对于题目的圆满解决是十分必要的,根据题目的结构关系,压轴题常分为下列三种类型.
一、“串联式”结构
“串联式”结构的压轴题,除了总条件“统领”全题外,前一个分题的结论,可以作为后一个分题的条件来使用,没有前一分题解(证)的结论,就无法解(证)下一个分题.
它的结构示意图如图1所示.

图1
例1 (2012年山东临沂市中考)如图2,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
分析:本题融合了函数解析式的确定、等腰三角形的判定等知识.主要考查了学生的阅读理解能力、分类讨论能力、逻辑推理能力,难度较大,具有一定的选拔功能.
解:(1) 如图2,过点B作BC⊥x轴,垂足为C,则∠BCD=90°.
因为∠AOB=120°,所以∠BOC=60°.
又因为OA=OB=4,
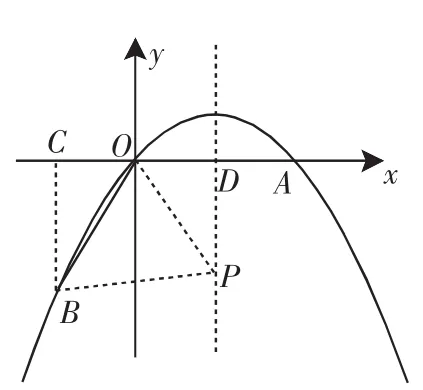
图2
所以点B的坐标是(-2,-2).
(2)因为抛物线过原点O和点A、B,所以可设抛物线的解析式为y=ax2+bx.
(3)存在,如图2,抛物线的对称轴是x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y).
①若OB=OP,则22+y2=42,解得y=±2.
当y=2时,在Rt△POD中,∠PDO=90°,sin∠POD=,所以∠POD=60°.
所以∠POB=∠POD+∠AOB=60°+120°=180°.
即P、O、B三点在同一条直线上,所以y=2不合题意,舍去.
所以点P的坐标为(2,-2).
②若OB=PB,则42+(y+2)2=42,解得y=-2.
所以点P的坐标为(2,-2).
③若OP=BP,则22+y2=42+(y+2)2,解得y=-2.
所以点P的坐标为(2,-2).
综上,符合条件的点P只有1个,其坐标为(2,-2).
点评:由于“串联式”结构的压轴题上下呈承接关系,所以需强调解题的正确性,显然如前一分题解答有误,则解答以后几个分题,将会劳而无功,另外这种题型若前一分题不会解(证),亦可拿前一分题的结论来解(证)下一分题,结果仍然有效.
二、“并联式”结构
“并联式”结构的压轴题,总条件“统领”每一个分题,但每一个分题却又是“独立”,呈并列关系,它的结构示意图如图3所示.
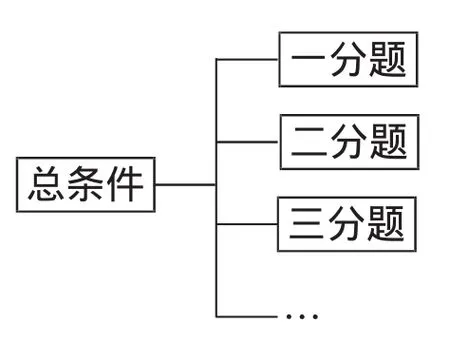
图3
例2 (2012年宁夏回族自治区中考)如图4,在矩形ABCD中,AB=2,AD=3,P是BC上的任意一点(P与B、C不重合),过点P作AP⊥PE,垂足为P,PE交CD于点E.
(1)连接AE,当△APE与△ADE全等时,求BP的长;
(2)若设BP为x,CE为y,试确定y与x的函数关系式,当x取何值时,y有最大值?最大值是多少?
(3)连接BD,若PE∥BD,试求出此时BP的长.
分析:本题综合考查了利用二次函数求最值、相似三角形、一元二次方程等知识.
解:(1)因为△APE≌△ADE,所以AP=AD=3.
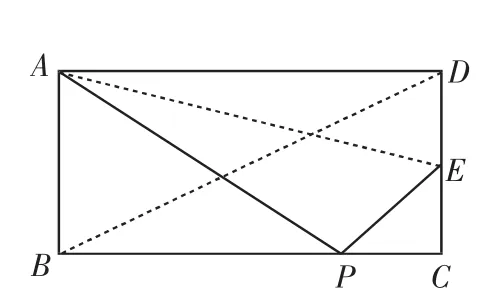
图4
在Rt△ABP中
(2)因为AP⊥PE,所以Rt△ABP∽Rt△PCE,
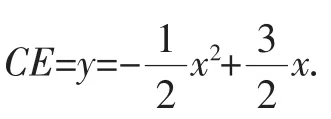
若PE∥BD,则△CPE∽△CBD.
整理得3x2-13x+12=0,
点评:本题的三个分题除总条件不变外,分题的条件各不相同,所以前一个分题的结果不能成为后一分题的条件,这种结构的压轴题,做对任何一分题都是有效的,都能得分,即使前一分题不会做或做错了,也不影响下一分题的解答或得分.
三、“混联式”结构
“混联式”结构的压轴题,除总条件仍“统领”每一个分题外,有的分题也“统领”下一个分题,分题与分题间既有承接关系,又有并列关系.它的结构示意图如图5所示.
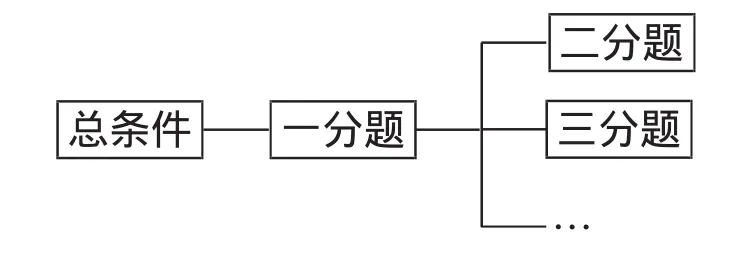
图5
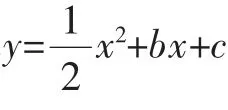
(1)求抛物线的解析式;
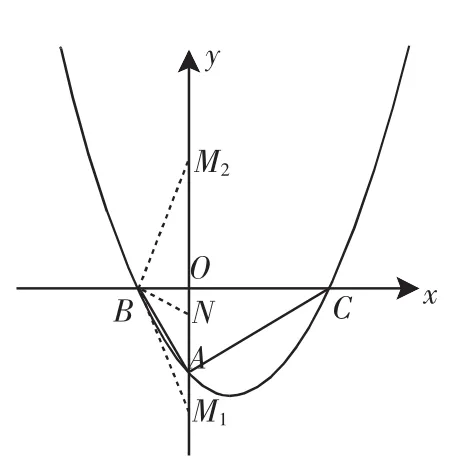
图6
(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.
分析:本题考查了二次函数的性质、平移、相似三角形等知识.第(1)问将A、B两点坐标代入即可求该抛物线的解析式.第(2)问先求出直线AB、AC的解析式,再根据平移条件,表示出平移后的二次函数的解析式,用含m的代数式表示出其顶点坐标,将坐标代入直线AB、AC的解析式中,即得到两个极端值,从而确定点P在△ABC内时m的取值范围.第(3)问先在OA上取点N,使得∠ONB=∠ACB,所以只需使∠NBA=∠OMB即可,从而确定在y轴的正负半轴上都有一个符合条件的M点,然后证△ABN与△AMB相似,通过相关比例线段求出AM的长.
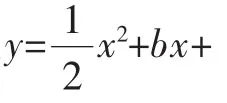
(2)由题意得,新抛物线的解析式可表示为
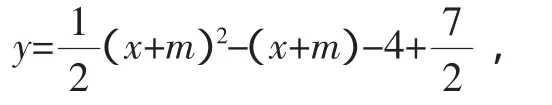
它的顶点坐标P(1-m,-1),由(1)的抛物线解析式可得C(4,0),那么直线AB的解析式为y=-2x-4,直线AC的解析式为y=x-4.

当点P在直线AC上时,(1-m)-4=-1,解得m=-2.
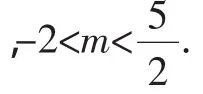
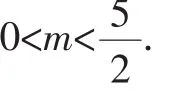
(3)由A(0,-4)、C(4,0)得OA=OC=4,且△OAC是等腰直角三角形.
如图6,在OA上取ON=OB=2,则∠ONB=∠ACB=45°.
所以∠ONB=∠NBA+∠CAB=∠ACB=∠OMB+∠OAB,即∠OMB=∠NBA.
在△ABN1、△AM1B中,∠BAN=∠M1AB,∠ABN=AM1B,所以△ABN∽△AM1B.
所以AB2=AN·AM1,
易得AB2=(-2)2+42=20.
AN=OA-ON=4-2=2,
所以AM1=20÷2=10.
所以DM1=AM1-OA=10-4=6.
而∠BM1A=∠BM2A=∠ABN,
所以OM1=OM2=6,AM2=OM2-OA=6-4=2.
综上所述,AM的长为10或2.
点评:“混联式”结构的压轴题,特别要搞清分题与分题之间的关系,即前一个分题的条件或结论,下一个分题能否使用,就要搞清分题与分题间是“串联”关系的结构,还是“并联”关系的结构,万不可盲目乱用,徒劳无功.

