GPS/INS组合定位中INS消噪模型研究
王建鹏
(1.中国矿业大学 (北京),北京 100083;2.山西焦煤集团杜儿坪矿,山西 太原 030026)
GPS/INS组合导航中,噪声的存在是制约导航精度提高的重要原因。从频域角度,可以将组合导航的噪声分为高频噪声和低频噪声。在高频噪声的消除方面,低通滤波器和小波等基于频率域的消噪方法体现了一定的优势,但对于低频噪声(偏心误差、尺度误差),由于运动体自身的运动信息也属于低频部分,所以很难将有用的信息和低频噪声分离开来,增加了噪声消除的难度。
考虑以上因素,本文首先对静态数据(不含运动信息)建模,以确定出误差模型参数,再将此模型运用到动态数据中进行消噪。针对于噪声分为高频噪声和低频噪声两部分,而且是在静态数据的基础上建模,所以首先采用小波理论消除高频噪声,再运用基于AR模型的KALMAN滤波对低频噪声建立合适的模型,通过实验选取最佳的模型参数。
1 滤波方法的简要比较
目前,有效的滤波方法主要有公式解析滤波、均值滤波、小波去噪等[1],先将这些方法的优缺点比较如下:①公式解析滤波。消除高频噪声效果好,但是滤波结果的误差较大、稳定性差;②中值滤波。能有效保持边沿频带信息,但消噪能力不强;③小波滤波。小波滤波介于公式解析和中值滤波之间,但是应用条件狭窄、滤波结果存在频率偏斜;④K alman滤波。自适应能力强,可与AR模型算法相结合实现良好的滤波消噪效果,本文基于AR模型,应用KALMN滤波算法对GPS/INS组合定位中INS进行消噪处理。
2 基于AR模型的KALMN滤波
平稳随机序列表示序列的统计特性不随时间的平移而变化,即均值和协方差不随时间的平移而变化。平稳白噪声序列是一种最基本的平稳序列。
下面介绍一种重要的平稳时间序列—ARMA时间序列[2-3],ARMA时间序列分为三种类型:①AR模型,即AR(p)自回归序列;②MA序列,即MA(q)滑动平均序列;③ARMA序列,即ARMA(p,q)自回归滑动平均序列。
2.1 ARMA时间序列的定义
ARMA(p,q)序列
设{Xt,t=0,±1,±2,…}是零均值平稳序列,满足式(1)。

式中,Xt是零均值、方差是的平稳白噪声,则称Xt是阶数为p,q的自回归滑动平均序列,简记为ARMA(p,q)序列。当q=0时,它是AR(p)序列;当p=0时,它为MA(q)序列。
2.2 KALMAN 滤波
卡尔曼滤波器卡用于估计离散时间控制过程的状态变量x∈。离散时间过程的描述见参考文献[4-5]。卡尔曼滤波器可分为时间更新方程和测量更新方程两个部分。时间更新方程也可视为预估方程,测量更新方程可视为校正方程。时间更新方程和测量更新方程的具体形式如下[6]式(2)~(6)所示。

测量更新方程首先做的是计算卡尔曼增益Kk。其次,便测量输出以获得zk,然后按式(5)产生状态的后验估计。最后按式(6)估计状态的后验协方差。计算完时间更新方程和测量更新方程,整个过程再次重复[7]。上一次计算得到的后验估计被作为下一次计算的先验估计。
3 小波消噪及尺度选取
影响IMU精度的噪声来源包括两部分:低频噪声和高频噪声。两种噪声存在一定的重叠共同影响着导航系统精度。高频噪声部分具有白噪声的特性,低频噪声具有一定的自相关性。
具有自相关性的低频噪声可以运用各种模型进行模型化,但是高频白噪声不具有此种特性,所以可以运用基于频率域的小波消噪消除一定频率范围的白噪声,为AR模型的建立提供良好的数据基础[8]。
一个合适的小波尺度选取是基于信号的特征及滤波的具体要求。在对静态数据进行小波消噪中,根据消除高频噪声,保留有用信息来确定小波分解尺度。
从图1可以看出,静态IMU数据的频率分布较均匀,在11Hz和14Hz出有两个峰值,根据经验,截止频率定为3Hz,即对大于3Hz的白噪声进行消除。

图1 原始数据的频谱分析
比较图2,可以看出5层小波分解消噪可以较好得消除大于3 Hz的噪声,3层和4层小波分解中,高于3Hz的白噪声有较多残留,6层小波分解中,将大于2~3 Hz的噪声都消除了,由于在这部分频率域中含有较多的有用信息,所以选用5层小波分解消噪较合适。
4 AR模型参数确定
建立AR模型的关键在于阶数的选取,一般来讲,阶数越多,模型的精确度越高,但是计算量会大幅度增加,在运用KALMAN滤波时,计算量以几何级数增长;而且,经过实验验证,并不是所有情况下,增加模型阶数就会提高精确度,当两者不存在相关性时,增加阶数反而会导致建模误差增大。
分别选取3阶、4阶、5阶的AR模型建模,并运用KALMAN滤波进行滤波。AR模型建立的状态转移矩阵

式中:bk为低频误差(偏心);p为AR模型的阶数。
观测方程

式中:H为单位阵;B=(bk-p+1bk-p…bk-2bk-1bk)T。
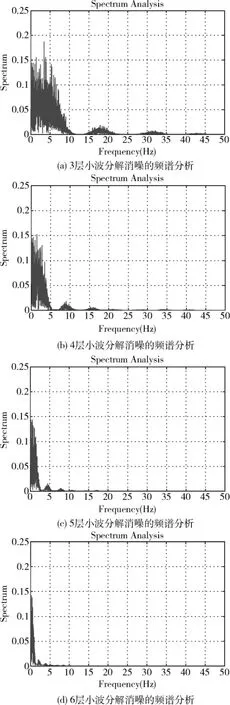
图2 小波分解消噪的频谱分析
比较图3,可以看出,用4阶AR模型的滤波效果要比用3阶和5阶的滤波效果要好,从160s开始,滤波值稳定于-0.0117,这就是静态数据的低频噪声(偏心值);3阶和5阶的AR模型滤波从100s后也趋于稳定,但是稳定值要比静态数据的观测值要大,主要是由于模型误差造成的[9-10]。
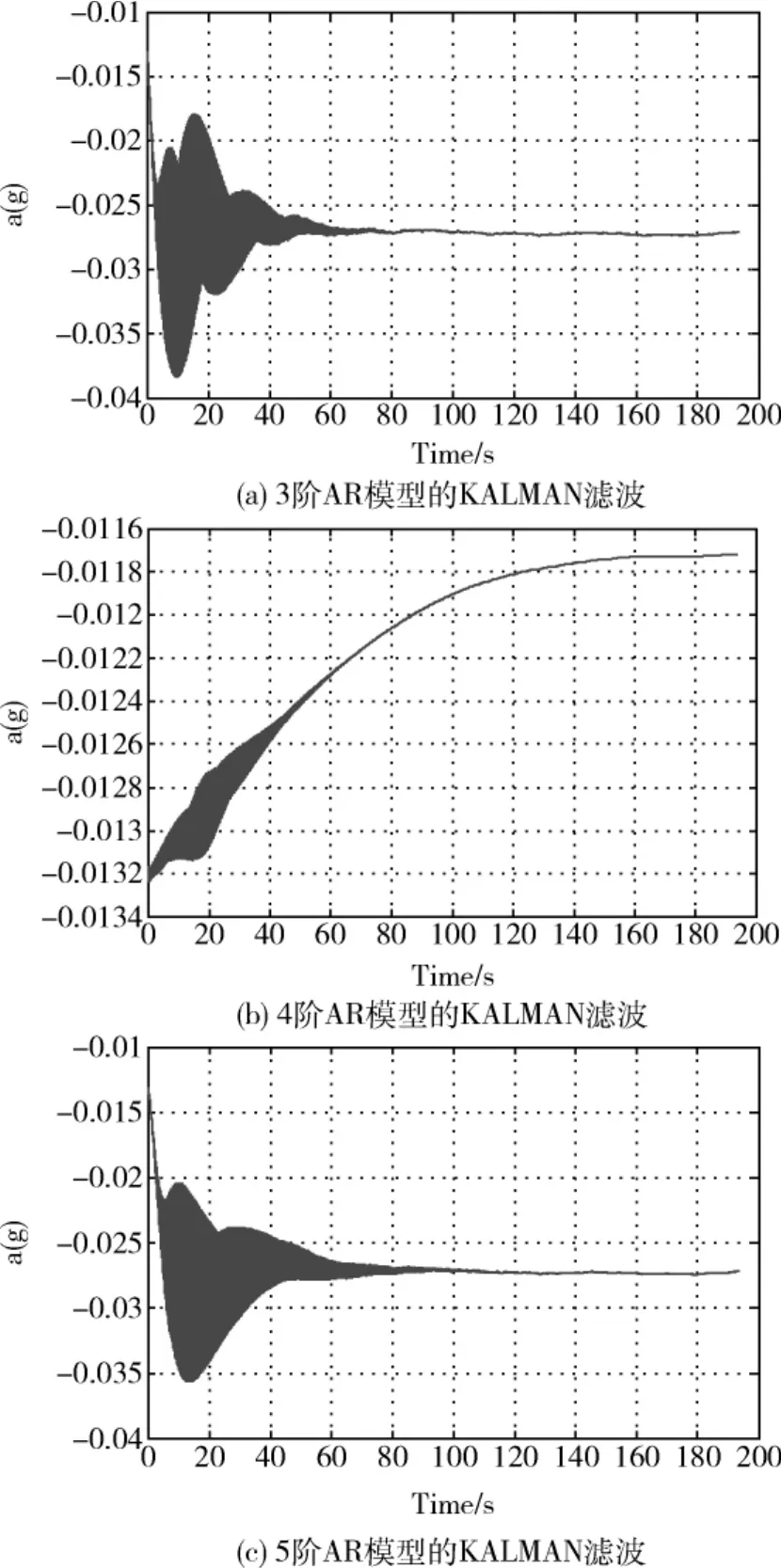
图3 AR模型的KALMAN滤波
5 结论
从IMU数据误差模型入手,分高频噪声和低频噪声两方面对IMU噪声进行消除,介绍了小波理论、低通滤波器和AR模型在IMU数据降噪方面的应用,并将其进行了对比,可得出以下结论。
1)在运用低通滤波器进行滤波时,关键点在于低通滤波器的设计,设计匹配性较高的低通滤波器可以提高消噪效果,低通滤波器要根据IMU自身数据特点及噪声频谱特性进行设计。
2)建立的基于AR模型的低频噪声模型,通过AR模型建立IMU静态数据的状态转移矩阵,运用KALMAN滤波求出低频噪声(偏心)。
3)运用IMU静态数据建立AR模型之前,可以借助小波,选择合适的分解层数去除高频噪声,对过滤后数据分析,找到合适的AR模型阶数及系数,为动态数据模型的建立提供一定的依据。
[1]王立琦,王铭义,张礼勇,等.谱估计中解析公式与卡尔曼滤波比较研究[J].哈尔滨工程大学学报,2010,31(1):115-119.
[2]张树京,齐立新.时间序列分析简明教程[M].北京:清华大学出版社,北方交通大学出版社,2003.
[3]练军想,汤勇刚,等.捷联惯导惯性系动基座对准算法研究[J].国防科技大学学报,2007,29(5):95-99.
[4]张显云,张勤,王利,等.基于卡尔曼滤波的AR模型及应用[J].测绘通报,2009(11):41-43.
[5]焉建国,陈正松,罗志才等.基于AR模型的上海地区地面沉降预测分析[J].大地测量与地球动力学,2009,29(5):121-124.
[6]吴富梅,杨元喜.基于高阶AR模型的陀螺随机漂移模型[J].测绘学报,2007,36(4):389-394.
[7]杨元喜,崔先强.动态定位有色噪声影响函数—以一阶AR模型为例[J].测绘学报,2003,32(1):6-10.
[8]金光明,张国良,陈林鹏,等.MEMS陀螺仪静态漂移模型与滤波方法研究[J].传感器与微系统,2007,26(11):48-50.
[9]沈晓蓉,张海,范耀祖,等.微捷联姿态系统的一种扩展卡尔曼滤波方法[J].北京航空航天大学学报,2007,33(8):933-935.
[10]秦庆强,张晓安,李艾华.基于自适应Kalman滤波的加速度计动态数据处理[J].计算机工程与设计,2009,30(17):3943-3945.

