基于形态分量分析与能量算子解调的齿轮箱复合故障诊断方法

李 蓉 于德介 陈向民

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

齿轮箱是机械系统中的重要部件，因其工作环境恶劣，且常处于高负荷下持续运行，故容易因疲劳磨损而发生局部故障。在工程实际中，故障往往不是单独出现的，某些故障常常会诱发其他故障的发生［1］，因此，对齿轮箱的复合故障进行研究具有重要的实际意义。

当齿轮箱中的齿轮出现局部故障时，齿轮的啮合频率及其谐波会被转频及其谐波调制；而当轴承出现局部故障时，轴承故障元件的固有频率会被故障元件的通过频率调制［2］。因此，对齿轮箱振动信号中的调制信息进行提取可为齿轮箱的故障诊断提供重要依据。常用的包络解调方法有广义检波滤波解调［3］、Hilbert包络解调［4］、能量算子解调等［5］。相对于 Hilbert解调，能量算子解调具有运算量小、解调精度高和响应速度快等优点［6－7］，被广泛应用于各种机械故障振动信号的调制信息提取。但当齿轮箱中同时出现齿轮局部故障和轴承局部故障时，由于齿轮故障信号的传递环节较多 （齿轮－轴－轴承－轴承座－测点）［2］，导致测点所测取的振动信号中齿轮故障成分往往比较微弱，其调制信息容易淹没在轴承调制信息中不易察觉，从而出现漏诊现象。因此，对齿轮箱复合故障信号中的各故障成分进行有效分离是齿轮箱复合故障诊断的关键。

最近，Starck等［8］基于信号的稀疏表示和形态多样性提出了形态分量分析（morphological component analysis，MCA），并在此基础上发展了扩展算法广义形态分量分析（generalized morphological component analysis，GMCA）。形态分量分析的主要思想是利用信号组成成分的形态差异性（可以由不同形态的字典稀疏表示）将信号中不同的形态成分进行分离［9］。该方法首先应用于图像处理［10－11］中图像几何结构部分与纹理部分的分离。近来，GMCA方法被引入机械故障诊断领域，并用于齿轮箱复合故障诊断［12－13］，取得了较好的效果。但GMCA方法需要同时采集多路传感器信号，在一定情况下会增加工程应用难度。而MCA方法能从单路传感器信号中分离出不同形态的信号成分，工程上应用更为简便，因此，本文利用MCA方法对齿轮箱复合故障振动信号进行分析。

基于上述分析，本文结合形态分量分析方法与能量算子解调方法，提出了一种基于形态分量分析与能量算子解调的齿轮箱复合故障诊断方法。齿轮局部故障往往会产生调幅调频成分，调幅调频成分幅值变化相对缓慢，可视为齿轮箱振动信号中的光滑成分（即结构部分）；而当轴承出现局部故障时，往往会产生周期性冲击成分，冲击成分幅值变化相对较快，可视为齿轮箱振动信号的细节成分（即纹理部分）。因此，当齿轮箱中同时出现齿轮局部故障和轴承局部故障时，可根据此形态差异实现二者的分离。本文对包含齿轮局部故障和轴承局部故障的齿轮箱复合故障进行了算法仿真和应用实例分析，结果表明，该方法能有效地分离齿轮故障特征和轴承故障特征。

1 形态分量分析

1.1 形态分量分析原理［8］

MCA算法可以看成是BP（basis pursuit）［14］和 MP（matching pursuit）［15］算法的结合，是一种组合稀疏表示理论模型，是稀疏表示理论的进一步发展。MCA算法的基本思想是，根据信号中各组成成分形态的差异，构建不同形态的稀疏表示字典，实现信号中各形态成分的分离。其基本原理如下。

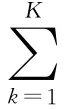
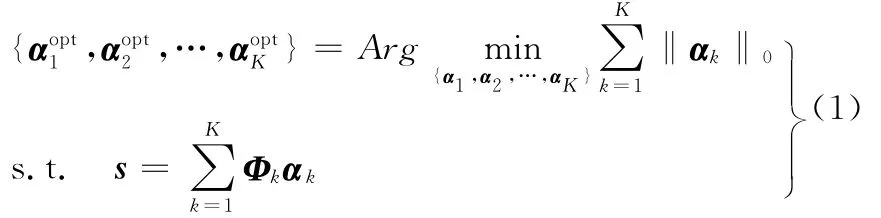
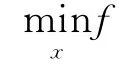
由于式（1）为非凸函数，难以求解，且算法复杂度随着字典列数的增加呈指数上升，因此，根据基追踪理论，将式（1）中的l0范数转化为l1范数以实现式（1）的优化求解，此时，式（1）转化为可优化求解的线性规划形式：

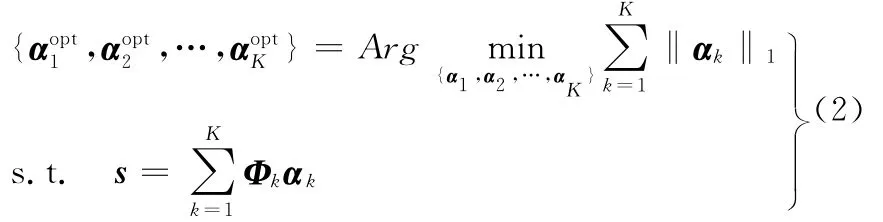
放宽式（2）的约束条件，可将式（2）转换为

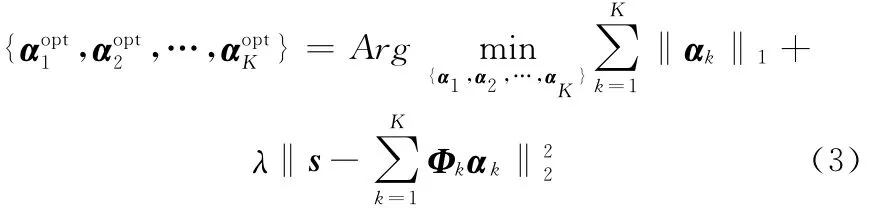
式中，λ为给定的阈值。

根据sk＝Φkαk，给定sk，便可以得到αk：

式中，为Φk的伪逆矩阵；rk为残余信号。

根据式（3）和式（4），可将式（1）中各变换系数｛α1，α2，…，αK｝的优化求解问题转化为下面各分量｛s1，s2，…，sK｝的优化求解问题：

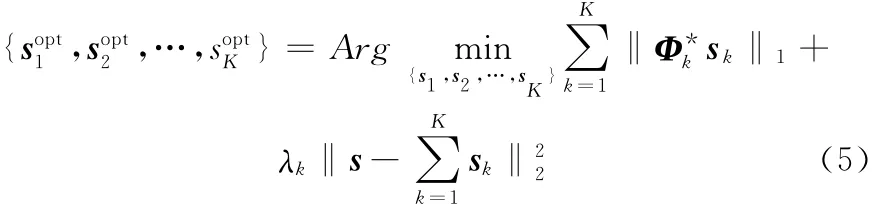
1.2 阈值函数的选择

对于式（5）的优化求解问题，Starck等［8］在BCR（block－coordinate－relaxation）算法的基础上，给出了MCA的数值实现步骤。在这一步骤中，变换系数αk的阈值去噪采用了软阈值方法：

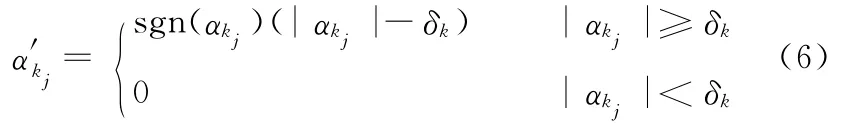
但由于软阈值方法在保证信号连续性的同时削弱了有用信号，故效果不佳。Bobin等［16］提出了一种 MOM（means of max）机制对 MCA的算法性能进行了改善，并在变换系数αk的阈值去噪处理上采用了硬阈值方法：

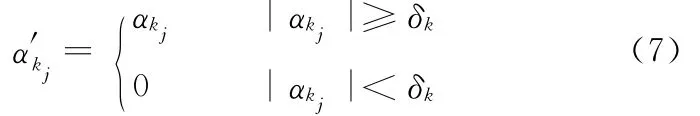
然而，硬阈值法在阈值点不连续，会给信号带来较大的方差。

针对软阈值和硬阈值的不足，Gao等［17］在对小波系数阈值去噪的研究中提出了一种折中的阈值去噪方法，即半软阈值方法：

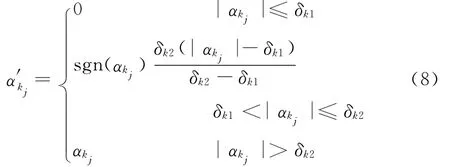
式中，δk2为上阈值；δk1为下阈值，一般δk2＝2δk1。

相对于软阈值和硬阈值，半软阈值能更有效地降低均方差，同时抑制噪声，较好地解决了抑制噪声与保留信号细节之间的权衡问题。因此，本文采用半软阈值方法对变换系数αk进行消噪处理。

2 能量算子解调［5，18］

具有时变幅值a（t）和时变相位ω（t）的调幅调频信号x（t）的一般表达式为

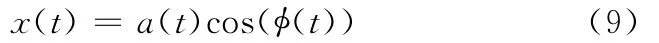
其能量算子定义为

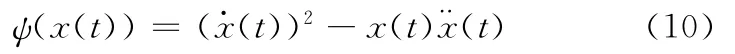
对式（9）求导得

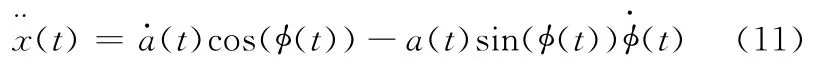
对式（11）求导得

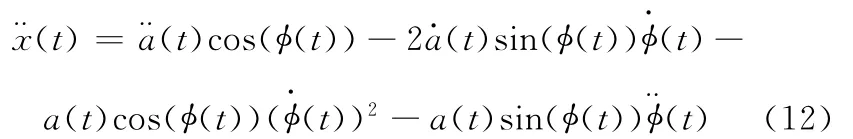
由于调制信号的变化比载波的变化慢得多，此时a（t）与ω（t）相对于载波的变化可近似为常数，即a·（t）＝0，a¨（t）＝0，φ¨（t）＝0。将式（11）、式（12）代入式（10）得

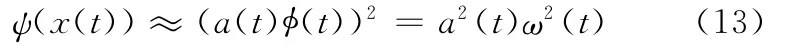
同理可得

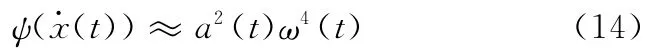
由式（13）、式（14）可求出信号的瞬时幅值a（t）和瞬时相位ω（t）：

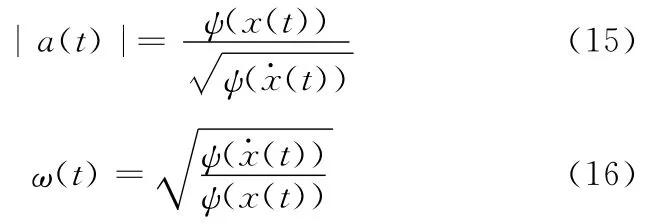
由式（15）、式（16）可知，调幅调频信号x（t）的瞬时幅值a（t）和瞬时频率ω（t）可由信号的能量函数ψ（x（t））和信号能量微分函数ψ（（t））近似确定。

3 算法流程

解调分析作为齿轮箱故障诊断的有力工具，可有效提取信号中的故障调制信息。但当齿轮箱出现复合故障时，其信号中包含了多种故障成分，且具有不同的调制特性。由于传统解调分析方法不适合解调多分量调制信号，直接对其进行解调分析容易出现虚假调制信息，且受故障损伤部位、故障损伤程度和故障信号传递路径的影响，在信号的解调谱中弱故障调制信息会被强故障调制信息所掩盖，不易察觉，从而出现漏诊现象，因此，本文结合形态分量分析方法和能量算子解调方法，提出了基于形态分量分析与能量算子解调的齿轮箱复合故障诊断方法。该方法首先构建局部离散余弦变换与离散正弦变换字典，用于稀疏表示信号中的谐振成分，同时，构建8阶消失矩Symlet小波字典，用以稀疏表示信号中的冲击成分；再利用MCA方法对包含齿轮局部故障和轴承局部故障的齿轮箱复合故障信号进行分析，得到包含齿轮故障信息的谐振分量、包含轴承故障信息的冲击分量和噪声分量（两分量之和与原始复合故障信号的差值）；最后分别对谐振分量和冲击分量进行能量算子解调分析，根据谐振分量的解调谱诊断齿轮故障，同时，根据冲击分量的解调谱诊断轴承故障。本文算法流程如图1所示。

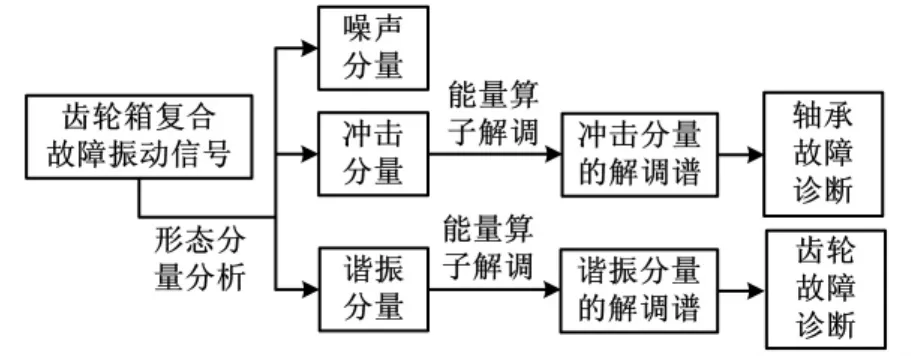
图1 算法流程图

4 算法仿真

为验证形态分量分析方法分离齿轮故障信号和轴承故障信号的有效性，设置的仿真信号x（t）如下：

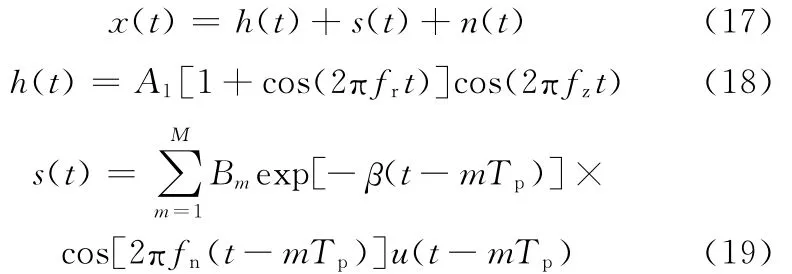
其中，h（t）为幅值调制信号，用以模拟齿轮故障信号，其载波频率fz被调制频率fr所调制；A1为幅值；s（t）表示周期冲击成分［19］，用以模拟轴承故障信号；s（t）由M个幅值为Bm、衰减系数为β、共振频率为fn的单冲击信号构成，冲击之间的时间间隔为Tp，即冲击出现的频率fo＝1/Tp；u（t）为单位阶跃函数；n（t）为噪声成分，用以模拟随机干扰。

取采样频率为4096 Hz，采样点数为4096，采样时长1s。将表1中各参数值代入式（18）和式（19），得到的仿真齿轮故障信号和仿真轴承故障信号分别如图2a和图2b所示。将式（18）和式（19）代入式（17），并加入幅值为0.7的随机噪声（图2c），得到的仿真合成信号如图3所示，可以看出，冲击信号已基本被淹没。

表1 仿真信号的各参数值

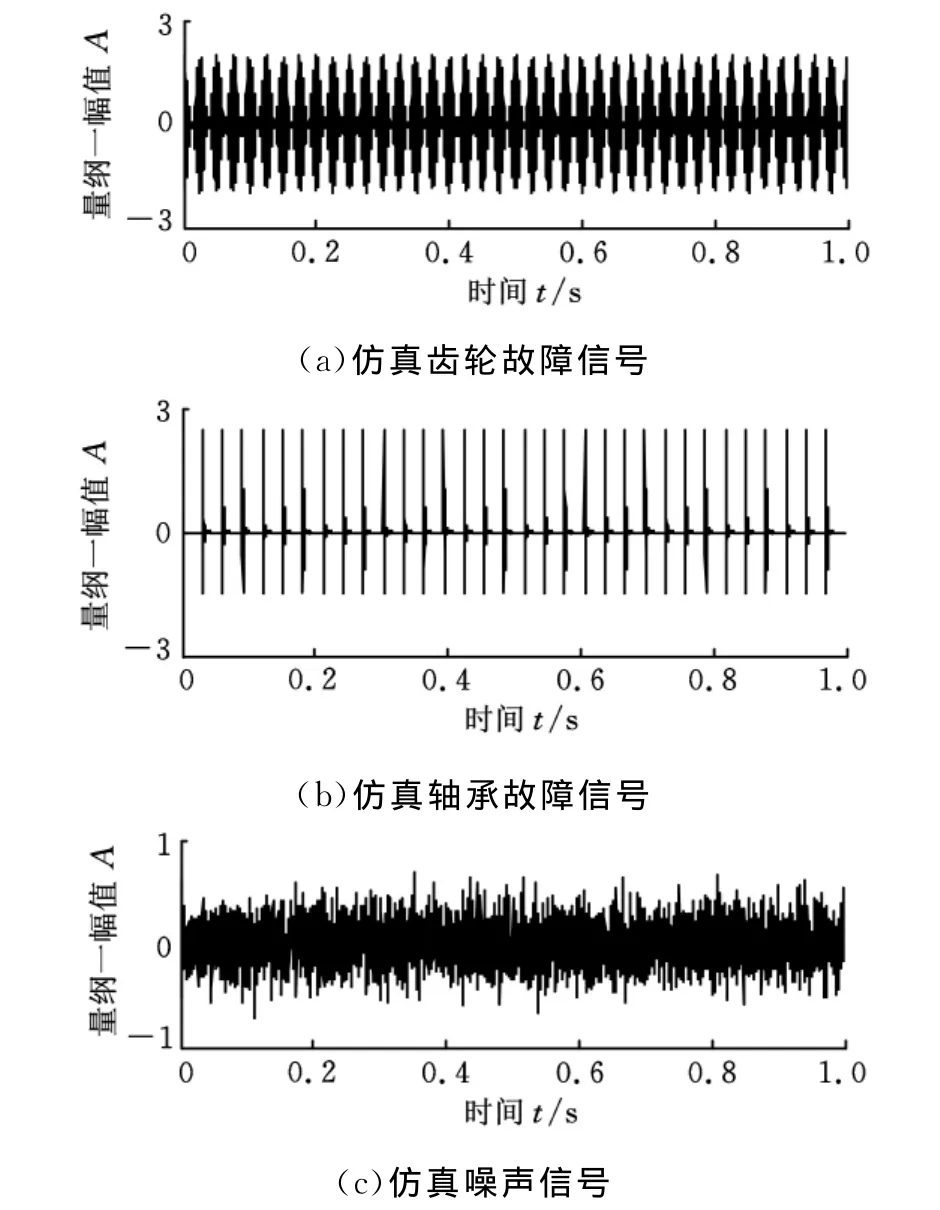
图2 各仿真信号时域波形

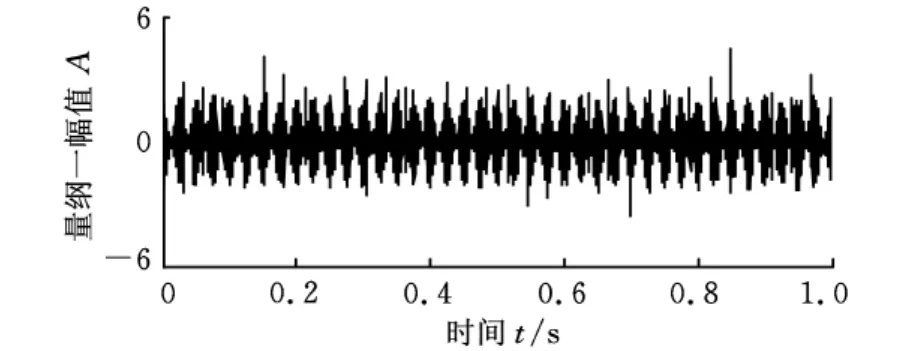
图3 仿真合成信号时域波形

对图3所示信号进行形态分量分析，得到的各分量如图4所示。对比图2与图4可知，谐振分量与冲击分量已基本分离，仅在信号幅值方面略有差异，表明了形态分量分析方法分离谐振分量与冲击分量的有效性。

对图4a、图4b所示分量进行能量算子解调分析，得到的解调谱分别如图5a、图5b所示。图5a中，在模拟转频fr处峰值明显，说明谐振分量中出现了转频调制现象；而从图5b可看出，在模拟轴承故障特征频率fo及其谐波处出现了明显峰值，表明出现了轴承故障，从而验证了方法的有效性。

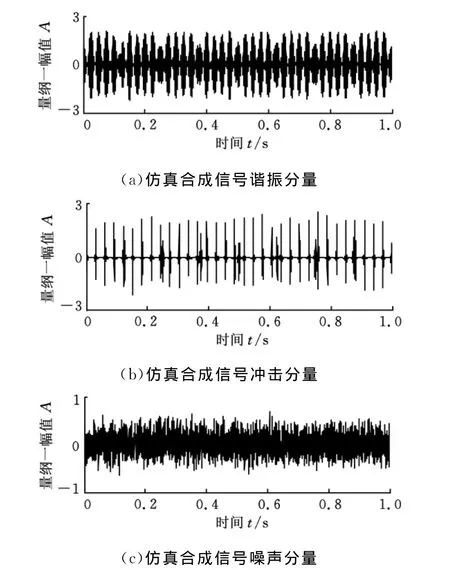
图4 仿真合成信号形态分量分析

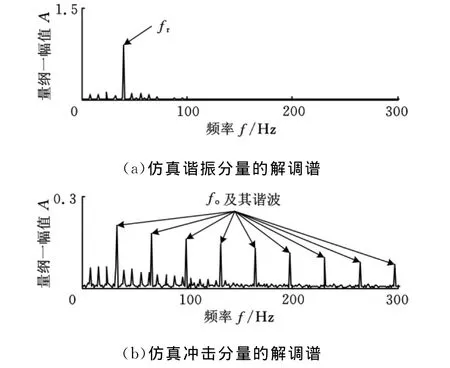
图5 仿真合成信号各分量的解调谱

对图3所示信号直接进行能量算子解调分析，得到的解调谱如图6所示，可看出，在模拟齿轮故障特征频率fr处峰值明显，而在模拟轴承故障特征频率处无显著峰值。对比图5和图6可知，利用形态分量分析对信号中各故障成分进行分离后再进行能量算子解调分析，能有效凸显信号中各故障特征。

5 应用实例

试验台为单级传动齿轮箱，其简图见图7。

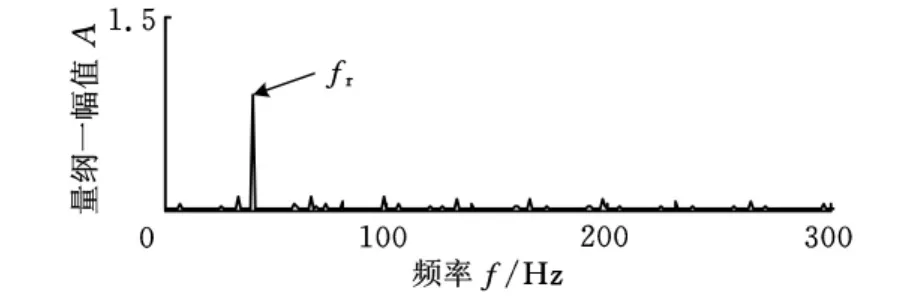
图6 仿真合成信号的解调谱

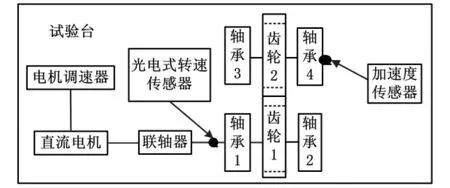
图7 试验台简图

试验齿轮为正齿轮，主动轴与从动轴齿数均为37。试验轴承1～轴承4均为SKF6307－2RS深沟球轴承，轴承参数见表2。

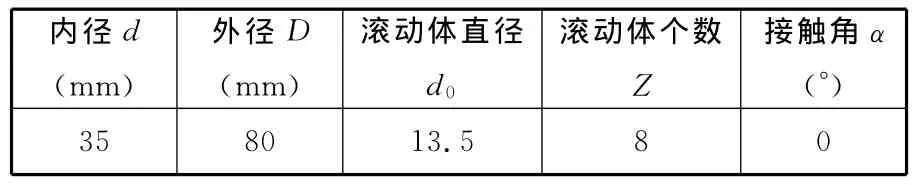
表2 轴承参数

为模拟齿轮箱齿轮、轴承复合故障，在齿轮2上整体切割掉一个齿，以模拟齿轮断齿局部故障；用激光在齿轮2齿根处切割宽0.15mm、深1mm的槽，以模拟齿轮裂纹局部故障；同时，用激光在轴承4的外圈上切割宽0.15mm、深0.13mm的槽，以模拟轴承外圈局部故障。为减小传递路径的影响，振动加速度传感器置于轴承4的轴承盖上，用以测取振动加速度信号。试验时，主动轴转速为600r/min，经计算，转频为10Hz，而轴承外圈故障特征频率为30.6 Hz。试验时用LMS数据采集设备采集振动加速度信号，采样频率为8192 Hz，采样点数为8192，采样时长为1s。

图8为齿轮2断齿故障与轴承4外圈故障的振动信号时域波形图，图中存在着冲击成分。

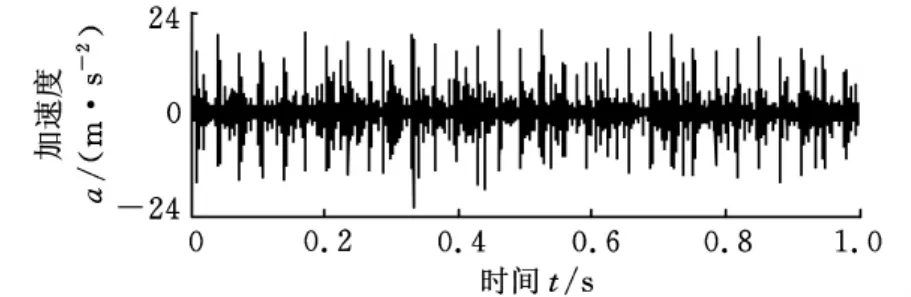
图8 齿轮断齿与轴承外圈复合故障振动信号

利用本文方法对图8所示信号进行分析，得到的各解调谱如图9所示。图9a中，在转频fr处存在明显的峰值，表明谐振分量中出现了转频调制现象，与齿轮断齿故障相符；而图9b中，在轴承外圈故障频率fo及其谐波处出现了明显的峰值，说明齿轮箱中出现了轴承外圈故障。

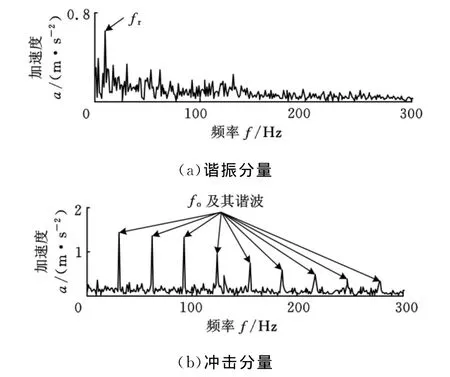
图9 齿轮断齿与轴承外圈复合故障的各分量解调谱

图10所示为直接对齿轮断齿与轴承外圈复合故障振动信号进行能量算子解调得到的解调谱，可看出，在外圈故障特征频率fo及谐波处出现了明显峰值，但转频处的峰值不明显，即只能诊断出轴承故障而不能诊断出齿轮故障。

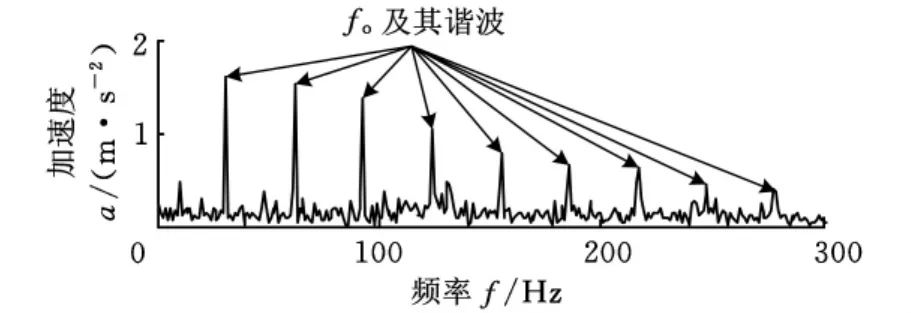
图10 齿轮断齿与轴承外圈复合故障振动信号的解调谱

图11所示为齿轮2裂纹故障与轴承4外圈故障的振动信号时域波形图，可看出，冲击不明显。

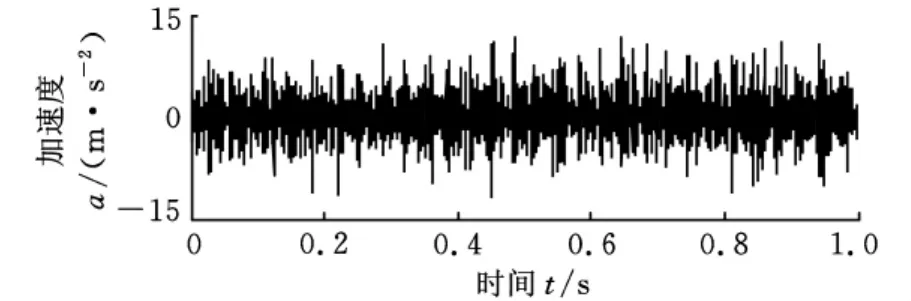
图11 齿轮裂纹与轴承外圈复合故障振动信号

利用本文方法对图11所示信号进行分析，得到的各解调谱如图12所示。图12a中，在转频fr处峰值突出，说明信号中出现转频调制现象，与齿轮裂纹故障特征相符；图12b中，在轴承外圈故障特征频率fo及其谐波处峰值明显，表明出现了轴承外圈故障。

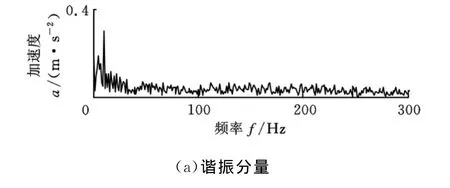
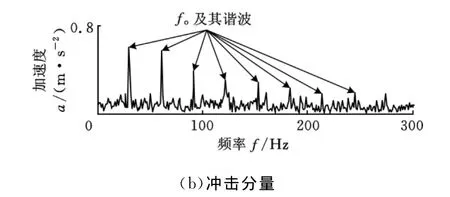
图12 齿轮裂纹与轴承外圈复合故障信号的各分量解调谱

图13所示为直接对齿轮裂纹与轴承外圈复合故障振动信号进行能量算子解调分析得到的解调谱，图中，在转频fr、轴承外圈故障特征频率fo及其谐波处出现了峰值，说明同时出现了齿轮和轴承外圈故障。但对比图12与图13可知，利用形态分量分析对故障信号中不同形态的故障成分进行分离后再进行能量算子解调分析，更能突显各故障的故障特征。

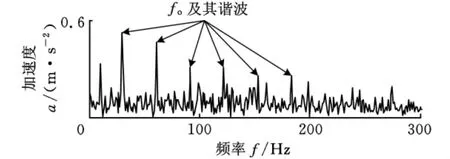
图13 齿轮裂纹与轴承外圈复合故障振动信号的解调谱

6 结语

本文结合形态分量分析与能量算子解调方法，提出了基于形态分量分析与能量算子解调的齿轮箱复合故障诊断方法，用于从单路传感器齿轮箱复合故障振动信号中分离齿轮故障特征和轴承故障特征，算法仿真和应用实例表明，利用本文方法对包含齿轮局部故障和轴承局部故障的齿轮箱复合故障振动信号进行分析，能有效地分离齿轮故障特征和轴承故障特征。本文将形态分量分析用于单路齿轮箱复合故障振动信号的形态成分分离，取得了一些效果，但还有很多地方尚需进一步研究，如稀疏表示字典的自适应优化选择、阈值去噪函数的进一步优化、多形态成分的分离等。

［1］张含蕾，周洁敏，李刚.基于小波分析的感应电动机复合故障诊断［J］.中国电机工程学报，2006，26（8）：159－162.

Zhang Hanlei，Zhou Jiemin，Li Gang.Mixed Fault Diagnosis Based on Wavelet Analysis in Induction Motors［J］.Proceedings of the CSEE，2006，26（8）：159－162.

［2］丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术［M］.北京：机械工业出版社，2005.

［3］张帆，丁康.广义检波解调分析的三种算法及其局限性研究［J］.振动工程学报，2002，15（2）：243－248.

Zhang Fan，Ding Kang.Research on the Three Algorithms and Limitations of Generalized Detectionfiltering Demodulation Analysis［J］.Journal of Vibration Engineering，2002，15（2）：243－248.

［4］胡清忠，褚福磊.基于Hilbert解调的滚动轴承故障诊断分析［J］.振动与冲击，2010，29（S）：242－244.

Hu Qingzhong，Chu Fulei.Analysis of Rolling Bearing Fault Diagnosis Based on Hilbert Demodulation［J］.Journal of Vibration and Shock，2010，29（S）：242－244.

［5］Teager H M.Some Observations on Oral Air Flow during Phonation［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1980，28（5）：599－601.

［6］刘红星，陈涛，屈梁生，等.能量算子解调方法及其在机械信号解调中的应用［J］.机械工程学报，1998，34（5）：85－90.

Liu Hongxing，Chen Tao，Qu Liangsheng，et al.Energy Operator Demodulating Approach and Its Application in Mechanical Signal Demodulations［J］.Chinese Journal of Mechanical Engineering，1998，34（5）：85－90.

［7］程军圣，于德介，杨宇.基于EMD的能量算子解调方法及其在机械故障诊断中的应用［J］.机械工程学报，2004，40（8）：115－118.

Cheng Junsheng，Yu Dejie，Yang Yu.Energy Operator Demodulating Approach Based on EMD and Its Application in Mechanical Fault Diagnosis［J］.Chinese Journal of Mechanical Engineering，2004，40（8）：115－118.

［8］Starck J L，Moudden Y，Robin J.Morphological Component Analysis［J］.Proceedings of SPIE，2005，59（14）：1－15.

［9］李映，张艳宁，许星.基于信号稀疏表示的形态成分分析：进展和展望［J］.电子学报，2009，37（1）：146－152.

Li Ying，Zhang Yanning，Xu Xing.Advances and Perspective on Morphological Component Analysis Based on Sparse Representation［J］.Acta Electronica Sinica，2009，37（1）：146－152.

［10］Starck J L，Elad M，Donoho D.Redundant Multiscale Transforms and Their Application for Morphological Component Separation［J］.Advances in Imaging and Electron Physics，2004，132（82）：287－384.

［11］Elad M，Starck J L，Querre P.Simultaneous Cartoon and Texture Image Inpainting Using Morphological Component Analysis（MCA）［J］.Journal on Applied and Computational Harmonic Analysis，2005，19（3）：340－358.

［12］杨杰，郑海起，关贞珍，等.基于形态成分分析的轴承复合故障诊断［J］.轴承，2011（8）：38－42.

Yang Jie，Zheng Haiqi，Guan Zhenzhen，et al.Compound Fault Diagnosis for Bearings Based on Morphological Component Annlysis［J］.Bearing，2011（8）：38－42.

［13］李辉，郑海起，唐力伟.基于改进形态分量分析的齿轮箱轴承多故障诊断研究［J］.振动与冲击，2012，31（12）：135－140.

Li Hui，Zheng Haiqi，Tang Liwei.Bearing Multifault Diagnosis Based on Improved Morphological Component Analysis［J］.Journal of Vibration and Shock，2012，31（12）：135－140.

［14］Chen S S，Donoho D L，Saunders M A.Atomic Decomposition by Basis Pursuit［J］.SIAM J.Sci.Comput.，1998，20（1）：33－61.

［15］Mallet S G，Zhang Z F.Matching Pursuit with Time－frequency Dictionaries［J］.IEEE Transaction on Signal Processing，1993，41（12）：3397－3415.

［16］Bobin J，Starck J L，Fadili J.Morphological Component Analysis：an Adaptive Thresholding Strategy［J］.IEEE Transaction on Image Processing，2007，16（11）：2675－2681.

［17］Gao Hongye，Bruce A G.Waveshrink and Semisoft Shrinkage［J］.Sta.Sci.Research Report，1995，39：5－8.

［18］陈向民，于德介，任凌志，等.基于线调频小波路径追踪阶比能量解调的齿轮轮齿裂纹故障诊断［J］.中国机械工程，2011，22（21）：2598－2563.

Chen Xiangmin，Yu Dejie，Ren Lingzhi，et al.Order Energy Demodulating Approach Based on Chirplet Path Pursuit and Its Application to Gear Tooth Crack Fault Diagnosis［J］.China Mechanical Engineering，2011，22（21）：2598－2563.

［19］Liang M，Bozchalooi I S.An Energy Operator Approach to Joint Application of Amplitude and Frequency－demodulations for Bearing Fault Detection［J］.Mechanical Systems and Signal Processing，2010，24（5）：1473－1494.