七自由度自动铺丝机器人的自运动流形分析

葛新锋

许昌学院，许昌，461000

0 引言

在飞机S形进气道的制造过程中，采用了先进的纤维丝束自动铺放技术。纤维丝束自动铺放主要由机器人的末端执行器在芯模上根据预先规划的轨迹来完成［1］。要在芯模上进行铺放纤维丝束，机器人所需要的自由度数至少为6，但是一般六自由度的机器人不能以任意姿态来跟踪芯模的位置［2］。因此，一些学者就采用了增加自由度的方式来改善机器人跟踪目标的灵活性，这种额外增加的自由度称为冗余自由度，具有冗余自由度的机器人称为冗余自由度机器人［3－4］。冗余自由度机器人比六自由度机器人具有更高的灵活性、更精确的跟踪目标能力、更好的避障能力和避奇异能力［5－7］。因此，对自由度大于6的冗余自由度机器人的研究更有实际意义。

在自动铺丝束成形技术的复合材料制造过程中，铺丝过程采用七自由度的冗余度机器人来完成，也就是说，七自由度的冗余度机器人系统是整个自动铺丝束成形系统中的重要组成部分，具体的铺丝工艺都由它来实现，因此对冗余度自动铺丝机器人进行深入研究意义十分重大。对机器人来讲，运动学逆解是实现运动规划和运动控制的基础，对于冗余自由度机器人也是一样，所以要实现对冗余自由度自动铺丝机器人的运动规划和运动控制，首先需要解决的是运动学逆解的问题。冗余自由度机器人的自运动流形包含了机器人的全部逆解［8］，给出了逆解和末端执行器之间的映射关系，从本质上反映了冗余度机器人的自运动能力。

对于冗余机器人基于自运动流形的运动学逆解的求解，国内外的学者们提出了诸多算法，Moll等［9］通过在冗余度机器人的自运动流形上寻找最小能量曲线的方法，来实现机器人的最优轨迹规划；Muller［10］利用人工势场法在冗余度机器人自运动流形的切空间研究机器人的避障问题，并给出了5R串联机器人的自运动流形；Joel［11］给出了平面3R机构和空间4R机构的自运动流形，并得出Jacobian矩阵的零空间即是自运动流形的切空间的结论；赵建文等［12］采用自运动流形的方法从理论上分析了特殊结构的冗余度机器人的逆解，但对于其他结构类型的冗余度机器人也没有给出有效的运动学逆解算法。上述算法普遍存在运算量大、实时性较差、优化结果不一定最优、不能充分利用冗余的自由度、算法不稳定等缺点。

要得到冗余自由度机器人的自运动流形，首先要求出冗余自由度机器人的位置逆解。但是对于六自由度以上的冗余度机器人来说，其位置逆解很难得到［13］。冗余度自动铺丝机器人的全部逆解基于自运动流形得到，对分析其他类型的冗余度机器人逆运动学解有一定的借鉴意义。

1 铺丝机器人的拓扑结构分析

铺丝机器人由1个六自由度串联机械手和1个旋转芯模组成，如图1所示。根据等效运动的原理，把芯模坐标系和基座坐标系固连在一起，从而得到肩部1个转动关节、肘部3个移动关节和腕部3个关节的七自由度串联机器人，其拓扑结构如图2所示。按照标准D－H方法建立坐标系，D－H参数如表1所示。

图1 自动铺丝机器人的结构图

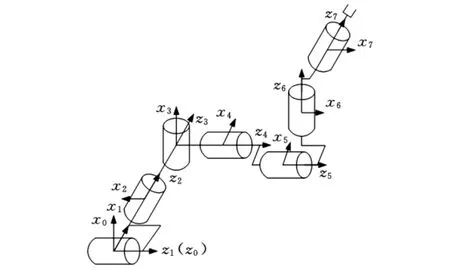
图2 七自由度自动铺丝机器人拓扑结构

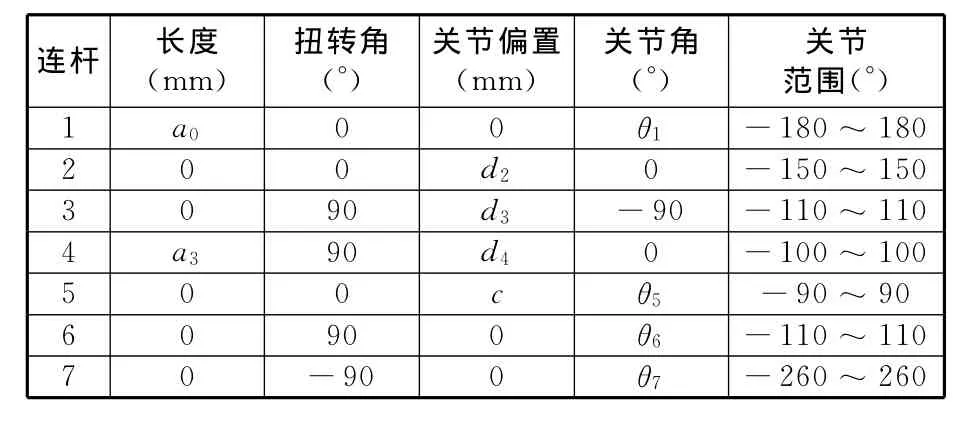
表1 铺丝机器人的连杆参数

2 七自由度机器人自运动流形

2.1 七自由度机器人位置关节空间流形

由于末端执行器与第7关节固连，通过第7关节坐标系的位置可以很容易知道末端执行器的位置。因此，末端执行器上固连运动坐标系的定义不会影响机器人的运动分析，故假定末端执行器的坐标系与第7关节坐标系重合。自动铺丝机器人的3个移动关节交于一点，决定了末端执行器的空间位置，这样末端执行器的位置就可以由第5、第6、第7关节轴线的交点到基坐标系原点之间的位移矢量l o1o4来确定，全体这样的l o1o4的集合就构成了该冗余度机器人的位置工作空间，所以3个移动关节又称为位置关节。

根据自动铺丝机器人的等效运动，可以定义腰肩肘关节构型空间为

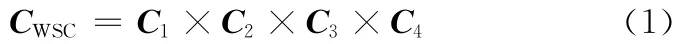
式中，C i为第i关节的构型空间，i＝1，2，3，4。

机器人的位置工作空间U p可以表示为

式中，f p（θp）为CWSC到U p的映射。

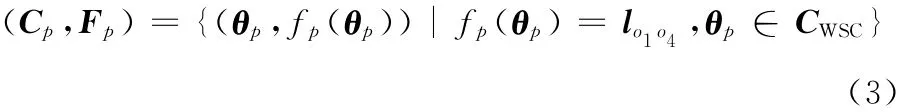
式中，C p为自动铺丝机器人的位置关节空间流形。

2.2 七自由度机器人姿态关节空间流形

腕部3个转动关节的轴线交于一点o4，末端执行器的姿态调整仅由第5、第6、第7关节的转动就可以实现，且姿态调整时不改变o4的位置，故腕部的3个转动关节又称为姿态关节，因此，该冗余度机器人的末端执行器是位姿解耦的。

定义腕关节构型空间：

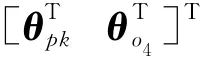
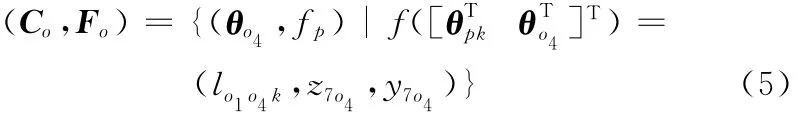
式中，C o为机器人的姿态关节空间流形；f为冗余度机器人的正向运动学解。

2.3 七自由度机器人自运动流形

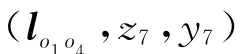
将第i关节的关节空间表示为C i，则关节构型空间C可以表示为7个独立的C i的积空间：

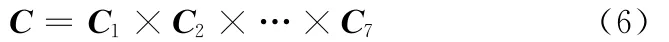
机器人关节所起的作用相当于数学里函数所起的作用，它实现了关节构型空间和末端执行器的位姿工作空间的映射与逆映射。令θ＝［θ1θ2…θ7］T，则冗余度机器人末端执行器的位姿工作空间可描述为

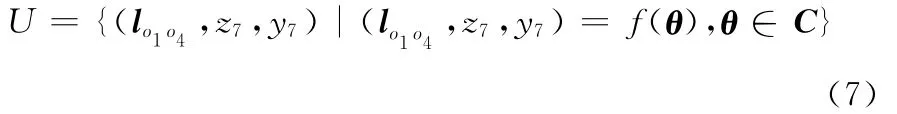
任取u∈U，则u对应的自运动流形可描述为由构型子空间C So和映射集F So组成的对子：

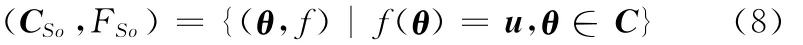
对于串联机器人而言，f很容易由θ求出，因此，求解机器人自运动流形的主要任务是求解C So。

3 自动铺丝机器人的自运动流形

自动铺丝机器人腕部的3个转动关节轴线交于一点，决定了机器人末端执行器在工作空间的姿态；3个移动关节交于一点，决定了机器人末端执行器在工作空间的位置。末端执行器的姿态调整可以仅由腕部的3个关节转动来实现，姿态调整时不改变末端执行器的位置。所以可以把该机器人的自运动流形分解为位置工作空间流形和姿态工作空间流形，并分别求取该位置的工作空间流形和姿态工作空间流形，然后经过配对得到该自动铺丝机器人关节空间的自运动流形。

3.1 自动铺丝机器人的位置关节空间流形

令末端执行器坐标系T相对芯模坐标系S的位姿变换矩阵为，则有

据前述可得位置关节参数：

根据等效运动原理，假设自动铺丝机器人末端执行器跟踪一个空间圆时，则应有图3所示的自动铺丝机器人位置关节空间流形，但在实际铺丝过程中，由于机器人末端执行器在工作过程中实际运动路线为一条空间曲线，加上待铺零件的尺寸限制，故位置关节空间流形仅为图3的一部分。

图3 位置关节空间流形

3.2 自动铺丝机器人的姿态关节空间流形

自动铺丝机器人末端的3个转动关节轴线交于一点，其几何结构如图4所示。末端执行器在坐标系x0y0z0中的期望坐标为（xee，yee，zee），3个转动关节轴线的交点到末端执行器的距离为l，ψ为末端执行器与其在x0y0面内的投影所在的平面和通过关节轴1的铅垂面的夹角。

图4 自动铺丝机器人姿态关节的几何结构

根据自动铺丝机器人姿态关节的几何结构，有下列等式成立：

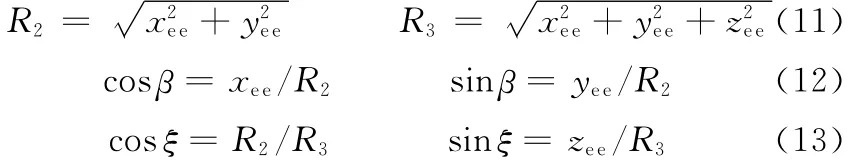
在给定末端执行器的位置坐标（xee，yee，zee）和自运动参数ψ的情况下，根据式（11）、式（12）、式（13）可得其运动学逆解：

其对应的姿态关节空间流形如图5所示（部分）。

3.3 自动铺丝机器人的自运动流形

图5 姿态关节空间流形

冗余自由度机器人的自运动流形是构型空间流形的子流形［14］，所以自动铺丝机器人的自运动流形由位置关节空间流形和姿态关节空间流形配对组合而成。机器人姿态关节空间流形为与机器人末端执行器位置和自运动参数有关的空间曲线，而机器人位置关节空间流形为－空心圆柱，故自动铺丝机器人的自运动流形为空心圆柱中空间曲线，所以七自由度冗余机器人能够以任意姿态完成铺丝任务。

4 自动铺丝机器人的自运动流形验证

为了验证求出的自运动流形的正确性，以铺丝机器人缠绕某型号飞机的S形进气道芯模为例进行验证，图6所示为某型号飞机的S形进气道机器人行走的轨迹曲线，也即图6为机器人末端执行器在芯模上的期望轨迹。图7所示是根据图6机器人期望轨迹的运动学逆解得到的末端操作器的仿真轨迹。

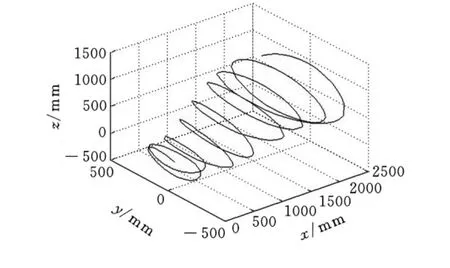
图6 末端执行器的期望轨迹

图7 末端执行器的仿真轨迹

对比图6和图7，发现所得到的仿真轨迹和期望轨迹相当一致，证明本文求得的自动铺丝机器人的自运动流形正确、适用。

5 结语

七自由度的自动铺丝机器人属于位姿解耦的冗余度机器人，其自运动流形可以看作是位置工作空间流形和姿态工作空间流形配对形成的自运动流形；求解位姿解耦的冗余度机器人的自运动流形时，先把自运动流形分解为位置工作空间流形和姿态工作空间流形，然后分别进行分析和求解，最后把求解出来的位置工作空间流形和姿态工作空间流形进行配对即可得到该冗余度机器人的自运动流形。

［1］刘亚威.F35战斗机进气道的自动化制造［J］.国防制造技术，2011（4）：32－34.

Liu Yawei.The Automated Manufacturing of the F35 Fighter Inlet［J］.Defense Manufacturing Technology，2011，4：32－34.

［2］韩振宇，邵忠喜，富宏亚，等.S形进气道纤维铺放轨迹网格化生成［J］.航空制造技术，2009（19）：72－78.

Han Zhenyu，Shao Zhongxi，Fu Hongya，et al.Meshing Method of Fiber Placement Track for SShaped Inlet［J］.Aeronautical Manufacturing Technology，2009（19）：72－78.

［3］王连圭，马保离.冗余机器人系统的自运动控制［J］.控制与决策，2003，18（2）：199－202.

Wang Liangui，Ma Baoli.Self－motion Control of Redundant Manipulators［J］.Control and Decision，2003，18（2）：199－202.

［4］张秋豪，孙汉旭，魏世民.改善冗余度机器人灵活性的研究［J］.北京邮电大学学报，2004，31（7）：748－752.

Zhang Qiuhao，Sun Hanxu，Wei Shimin.A New Method for Improving Flexibility of Redundant Robot［J］.Journal of Beijing University of Posts and Telecommunications，2004，31（7）：748－752.

［5］陆震.冗余自由度机器人原理及应用［M］.北京：机械工业出版社，2007.

［6］唐粲，贠超，栾胜.一种新型医疗机器人运动学及灵活性分析［J］.北京航空航天大学学报，2004，27（4）：74－77.

Tang Can，Yun Chao，Luan Sheng.Analysis of Kinematics and Dexterity for New Surgery Robot［J］.Journal of Beijing University of Aeronautics and Astronautics，2004，27（4）：74－77.

［7］贾庆轩，褚明，孙汉旭，等.9－DOF超冗余机器人轨迹规划优化算法［J］.北京邮电大学学报，2008，31（2）：20－25.

Jia Qingxuan，Chu Ming，Sun Hanxu，et al.Research on the Optimal Algorithm for Trajectory Planning of a 9－DOF Hyper－redundant Robot［J］.Journal of Beijing University of Posts and Telecommunications，2008，31（2）：20－25.

［8］Burdick J W.On the Inverse Kinematics of Redundant Manipulators：Characterization of the Self－Motion Manifolds［C］//IEEE International Conference on Robotics and Automation.New York：IEEE，Council on Robotics and Automation，1989：264－270.

［9］Moll M，Kavraki L E.Path Planning for Minimal Energy Curves of Constant Length［C］//Proceedings of the 2004 IEEE International Conference on Robotics and Automation.New Orleans：Institute of Electrical and Electronics Engineers，2004：2826－2831.

［10］Muller A.Collision Avoiding Continuation Method for Inverse Kinematics of Redundant Manipulator［C］//Proceedings of the 2004 IEEE International Conference on Robotics and Automation.New Orleans：Institute of Electrical and Electronics Engineers，2004：1593－1598.

［11］Joel W B.On the Inverse Kinematics of Redundant Manipulator：Characterization of the Self－motion Manifold［C］//Proceedings of the 1989 IEEE International Conference on Robotics and Automation.New York：IEEE，1989：264－270.

［12］赵建文，姚玉峰，黄博.一种位姿耦合式冗余度机器人的自运动流形［J］.机械科学与技术，2009，28（8）：1012－1017.

Zhao Jianwen，Yao Yufeng，Huang Bo.Self－motion Manifold of a Redundant Robot with Coupled Pose［J］.Mechanical Science and Technology，2009，28（8）：1012－1017.

［13］Moll M，Kavraki L E.Path Planning for Minimal Energy Curves of Constant Length［C］//Proceedings of the 2004 IEEE International Conference on Robotics and Automation.New Orleans：Institute of Electrical and Electronics Engineers，2004：2826－2831.

［14］Burdick J W.Kinematics Analysis and Design of Redundant Robot Manipulators［D］.California：Stanford University，1980.