受载复合材料曲板结构的失效特征研究
黄豪杰,张俊琪,刘龙权
(1.上海飞机设计研究院,上海 201210;2.上海交通大学 航空航天学院,上海 200240)
为降低航空航天飞行器的质量,航空航天飞行器的零件大多用薄壁板材结构.而纤维增强复合材料相比合金钢和铝合金等金属材料具有比强度高,比模量大,耐高温性好,性能可设计性强等诸多优点,在航空、航天、汽车、造船和交通等各个领域得到越来越广泛的应用[1-2].复合材料板材结构即包含曲率较小的、可以简化为平板的壁板类结构,也包含曲率较大的、用于传递非同向载荷的角片等曲板结构.由于受载复合材料曲板同时存在材料非线性、几何非线性以及加载过程中的偏心,使得其服役时承受较高的层间拉伸应力,再加上复合材料面外强度较低的特点,使得复合材料弯角结构极易出现分层,而导致其失效.
1 研究概况
国内外学者对受载曲板结构进行了大量的理论和试验研究.在理论分析方面有非常著名的铁摩辛柯弹性梁理论[3]和LEKHNITSKII关于曲梁分别承受纯弯和端部载荷时应力分布的解析计算方法[4].LIN 等人[5-6]建立了不同曲率的复合材料曲梁分别在轴向、剪切、径向和切向载荷下的变形解析表达式,并将计算结果与应用有限元方法的计算结果进行比较,一致性良好.但解析解只能针对理想的状态,不能考虑弯角结构与其他结构连接位置的不同以及复合材料铺层、缺陷和载荷引起的不同引起的非线性力学响应.
在试验方面,JACKSON和 MARTIN[7]等通过对复合材料L形梁进行拉伸试验,得到其面外拉伸强度;另外一些学者则通过对半圆形曲梁进行四点弯试验,在弯角区域产生纯弯载荷,从而得到复合材料的面外拉伸强度[8].这些试验方法在试验的难易程度以及试验数据的准确性方面各有优缺点,CUI等人[9]对这些方法进行了统计和评估.美国材料测试协会(American Society for Testing and Materials,ASTM)制定的试验标准 ASTM D 6415[10],则是通过对复合材料L形梁进行四点弯试验获得复合材料的面外拉伸强度.但所有以上试验方法只适合于得到复合材料弯角承受纯弯载荷时的面外拉伸强度,并不能代表复合材料弯角结构在飞机中的真实受力状态.美国NASA拉德利研究中心的MARTIN[11]开发了试验方法,较真实地模拟了曲梁在飞机结构中真实的受力状态,并对复合材料曲梁的失效载荷、失效模式进行了测试.
所有这些试验方法可以得到不同复合材料弯角构型在不同受力情况下的失效载荷,但单纯依赖试验方法比较昂贵,而且由于弯角区域面积较小,难以通过常规方法获得其受载时的应变和应力非线性变化过程,并进一步确定其设计准则.应用DIC(Digital image correlation)方法和摩尔干涉法虽然可以测得曲梁受载过程中层间应变分布,但此方法对于测量结果的准确性尚待进一步发展[12].而经过试验验证的有限元法不但可以得到复合材料受载过程中的应力和应变变化,而且比较省时、省力,有助于指导设计人员进行多参数优化设计,成为飞行器复合材料结构设计不可或缺的工具.因此有必要通过经过试验验证的有限元方法,得到弯角结构在不同的支持和加载条件下的应力分布特点,为设计和强度校核提供依据.
2 试验研究
2.1 试验件介绍
复合材料曲板试验件的几何尺寸如图1所示,其中长臂为100mm,短臂为40mm,宽度为50 mm,弯角区域的内径为5mm,短腿上2个孔直径均为6mm.试验件为Cytec公司的CMS-CP-301平纹编织复合材料,试验件沿厚度方向共10个铺层,由内向外铺层顺序为[(±45°)/(0°,90°)/(±45°)3]s(其中(±45°),(0°,90°)为复合材料单向带的铺设角度,下标“3”为重复铺设3层,下标“s”为对称).单层复合材料厚度为0.216mm,总的厚度为2.16mm.其单层力学性能参数见表1(材料力学性能数据来自美国Cytec公司).
表1中E,G,μ和S分别为弹性模量、剪切模量、泊松比和强度,下标L,T和Z分别代表编织复合材料的经向、纬向和厚度方向,上标T和C分别为拉伸和压缩方向.例如,EL代表编织复合材料经向弹性模量,STL代表编织复合材料经向的拉伸强度.
2.2 试验设置
本文研究的曲板试验件共6件,在试验件的内外侧分别粘贴两个应变片,以进行试验件安装对中,贴片位置如图2所示.
在CMT5105微机控制电子万能试验机上的安装和夹持方法如图3所示.为了模拟复合材料角片在结构中的实际应用,试验件一端固定在试验机的下夹头上,加持距离为20mm,另一端通过两个M5螺栓与刚度较大的夹具连接,并固定到试验机的上夹头上,上夹具的下表面到试验件上表面距离为10 mm.为实现准静态加载,试验采用速度为1mm·min-1的位移控制加载.通过VTI VXI1629数据采集系统测量载荷达到300N时的应变数据,根据4个通道的应变值判断试验件的对中情况,并通过调整图3中的2个螺母实现试验件的对中.试验终止条件为试验载荷下降到其最大载荷的50%.

表1 平纹编织复合材料单层力学性能Tab.1 Mechanical properties of the woven fabric ply
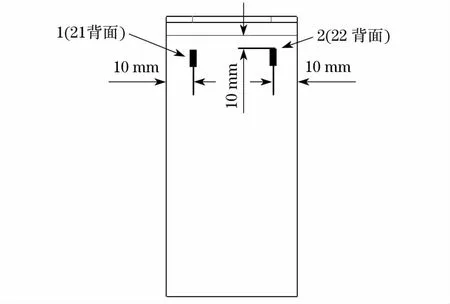
图2 试验件贴片位置Fig.2 Location of strain gauges

图3 试验装置Fig.3 Test setup
3 数值模拟
3.1 有限元模型
为研究曲板结构受载失效过程中复合材料内部的应力分布,本文运用ABAQUS软件建立了三维有限元模型,如图4所示.考虑到曲板结构受载过程中几何、材料和边界条件都关于xOy平面对称,为提高计算效率,只建立了一半模型.由于曲板区域是分层破坏的区域,所以网格划分较细,沿着1/4圆周方向划分90个单元,沿厚度方向划分10个单元,每层单元代表一个实际铺层.复合材料曲板结构共31 837个节点,27 324个C3D8R单元.另外还建立了螺栓和垫板,在对称面上施加对称约束,即约束对称面上节点的z向位移(Uz=0).曲板长臂(模型中长度为80mm)末端施加固支约束,即约束端部节点沿x,y和z向的位移 (Ux=Uy=Uz=0).在螺栓端面轴线处建立参考点,并在参考点与螺栓断面之间建立铰接耦合约束,通过参考点控制螺栓端面的运动.限制参考点在x和z方向的运动(Ux=Uz=0),并施加y方向的位移载荷.

图4 试验件有限元模型Fig.4 Finite element Model of the specimen
3.2 复合材料的渐进损伤分析
ABAQUS软件的非线性计算功能十分强大,用户可以根据模型的材料性能自定义本构关系,通过FORTRAN编译子程序,分析结构受载过程中的非线性特征.本文基于三维 Hashin[13]准则和文献[14]分层准则,结合文献[15-16]研究给出的渐进损伤和刚度折减方式,建立了复合材料编织结构的失效准则和刚度折减,通过应用USDFLD子程序,考虑了加载过程中复合材料的累积失效过程.具体如下.
3.2.1 失效准则
(1)经向纤维拉伸失效

式中:σ11,τ12,τ13分别为经向的正应力、面内剪应力和经向与厚度方向之间的面外剪应力.
(2)纬向纤维失效

式中:σ22,τ23分别为纬向的正应力和纬向与厚度方向之间的面外剪应力.
(3)分层失效
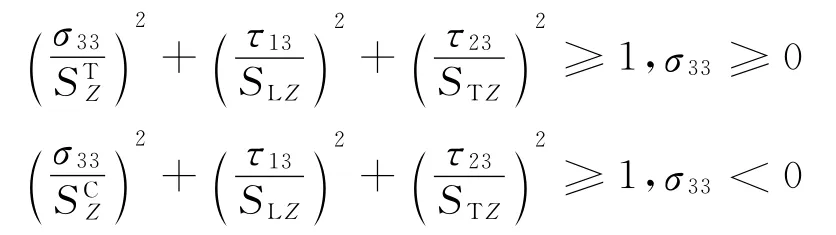
式中:σ33为厚度方向的正应力.
3.2.2 刚度折减
编织结构复合材料的刚度折减见表2.

表2 编织结构复合材料的刚度折减Tab.2 Degradation rules of the fabric composite
其中E′L,E′T,E′Z,μ′LT,μ′LZ,μ′TZ,G′LT,G′LZ,G′TZ分别为EL,ET,μLT,μLZ,μTZ,GLT,GLZ,GTZ折减后的弹性常数.
3.3 结果分析
3.3.1 载荷-位移曲线
根据试件的数值模拟结果与试验结果可以得到加载过程中的载荷-位移曲线,如图5所示,从中可以发现数值模拟结果与实验结果载荷位移曲线趋向吻合较好,试验得到的最大载荷为1 240N,有限元得到的最大载荷为1 307N,相对误差为5.1%.试验得到的破坏位移为2.97mm,有限元得到的破坏位移为3.15mm,相对误差为5.71%.从刚度和强度两个方面考虑,有限元模型均能较为准确的模拟曲板结构的受载过程.
3.3.2 失效过程
试验得到的分层起始和扩展情况如图6所示.分析图6发现,载荷达到一定值后,曲板区域突然出现几乎跨越全90°曲板区域的层间裂纹.但此时载荷并无下降,并且随着进一步加载,分层破坏沿周向扩展,当裂纹超出曲板的全部90°一定范围之后,裂纹开始出现在其他厚度位置.
3.3.3 弯角处应力分布
由于根据解析方法可知,曲板区域的应力在顺时针方向25°处达到最大[11],而且分层破坏主要由面外正应力σ33控制.不同载荷下,曲板区域顺时针方向25°的截面上,σ33沿着径向的分布如图7所示.可以发现不同载荷下,在径向随着半径的增大厚度方向应力都是先增大后减小,10个铺层中第4层和第5层之间节点应力最大.
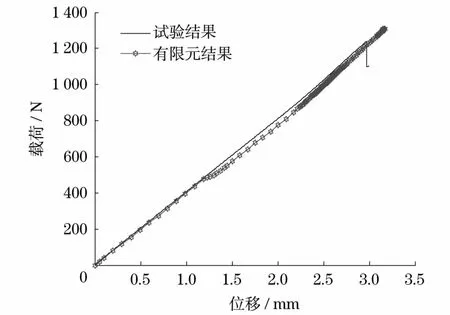
图5 试验与限元结果对比Fig.5 Comparisons between test and simulation results
半径为5.864mm(第4层与第5层之间)处,σ33沿着周向的分布如图8所示.从图8中可以发现,不同载荷下,在周向(顺时针)随着角度的增大厚度方向应力都是先增大后减小.但是在不同载荷下,最大应力并非处在相同的一个角度不变.当载荷为20N时,σ33的最大值出现在19°处;当载荷为600N时,σ33的最大值出现在20°处;当载荷为1 300 N时,σ33的最大值出现在21°处.即,随着载荷提高,最大面外应力出现的位置逐渐移向加载端.

图6 试验件破坏过程Fig.6 Failure process of the specimen

图7 面外应力σ33沿径向的分布Fig.7 Distribution of theσ33along the radial direction

图8 面外应力σ33沿周向的分布Fig.8 Distribution of theσ33along thecircumferential direction
4 结论
本文综合应用试验和数值模拟的方法,对平纹编织复合材料曲板结构在受载过程中的应力分布以及最终的破坏载荷、变形以及破坏模式进行了研究,可以得到如下结论.
(1)本文采用的数值仿真模型能够较为准确的模拟曲板结构的受载过程,与试验结果吻合较好.
(2)曲板结构受载过程中,弯角区域发生分层破坏,随着载荷的增大,分层会沿着径向和周向扩展.
(3)在特定的载荷水平下,弯角面外应力σ33沿着径向和周向,均呈现先增大后减小的分布趋势.
(4)随着外加载荷的增大,弯角区域厚度方向最大应力的位置发生了变化,逐渐向加载端移动.
[1]矫桂琼,贾普荣.复合材料力学[M].西安:西北工业大学出版社,2008.
JIAO Guiqiong,JIA Purong.Mechanics of composites[M].Xi’an:Northwestern Polytechnical University Press,2008.
[2]陈强,强宝民,何润生.几种参数对复合材料圆柱壳体振动特性的影响[J].中国工程机械学报,2007,5(4):394-398
CHEN Qiang,QIANG Baomin,HE Runsheng.Parametric impacts on vibration performance of composite cylindrical casing[J].Chinese Journal of Construction Machinery,2007,5(4):394-398.
[3]WANG M,LIU Y.Elasticity solutions for orthotropic functionally graded curved beams[J].European Journal of Mechanics-A/Solids,2013,37:8-16.
[4]LEKHNITSKII S G.Anisotropic plates [M].New York:Gordon and Breach Science Publishers,1968.
[5]LIN K C,HSIEH C M.The closed form general solutions of 2-D curved laminated beams of variable curvatures[J].Composite Structures,2007,79(4):606-618.
[6]LIN K C,HSIEH C M.Finite deformation of 2-D laminated curved beams with variable curvatures[J].International Journal of Non-Linear Mechanics,2011,46(10):1293-1304.
[7]JACKSON W C,MARTIN R H.An lnterlaminar tensile strength specimen[J].Astm Special Technical Publication,1993,1206:333-333
[8]IGE D,SARGEIT P.An apparatus for determining the interlaminar tensile strength of laminated composites using the curved specimen geometry[C]∥ECCM Composites Testing and Standardisation,European Materials,Amsterdam,1992:267-276.
[9]CUI W,LIU T,LEN J,et al.Interlaminar tensile strength(ILTS)measurement of woven glass/polyester laminates using four-point curved beam specimen[J].Composites Part A:applied science and manufacturing,1996,27(11):1097-1105.
[10]ASTM Committee.ASTM D 6415/D 6415M-06 Standard test method for measuring the curved beam strength of a fiber-reinforced polymer-matrix composite[R].American Society for Testing and Materials,2007.
[11]MARTIN R.Delamination failure in a unidirectional curved composite laminate[J].Composite materials:Testing and Design,1992,10:365-383.
[12]JOH D.A semi-micromechanic interlaminar strain analysis on curved-beam specimens[R].Missouri:National Aeronautics and Space Administration,1990.
[13]HASHIN Z.Failure criteria for Unidirectional fiber composite[J].Journal of Applied Mechanics,1980,47:329-334.
[14]YE L.Role of matrix resin in delamination onset and growth in composite laminates[J].Science and Technology,1988,33:257-277.
[15]CAMANHO P P,MATTHEWS F L.A progressive damage model for mechanically fastened joints in composite laminates[J].Journal of Composite Materials,1999,33(24):2248-2280.
[16]TSERPES K I,LABEAS G,PAPANIKOS P,et al.Strength prediction of bolted joints in graphite/epoxy composite laminates[J].Composites Part B:engineering,2002,33(7):521-529.

