空域滤波抗干扰性能的新型评定方法

李 琳，周文辉，谭述森

（1.北京卫星导航中心，北京 100094；2.北京系统工程研究所，北京 100101）

1 引言

为适应现代高技术战争集干扰与抗干扰、侦察与抗侦察、摧毁与抗摧毁为一体的新型作战样式，体现卫星导航系统功能性能的用户设备必须具有较强的抗干扰、抗侦察和抗摧毁能力，以确保卫星导航系统效能得以充分发挥［1-7，9］。

基于阵列天线自适应处理的空域滤波作为用户设备的主流抗干扰技术，具有对干扰类型、干扰带宽、非理想误差不敏感等优点［1-4，7，9］。但因基于零陷深度的性能评定方法在全面性、确切性等方面欠佳，继而功率反演、跟踪单星和跟踪多星等滤波算法的定量比较，以及阵元数目、间距、布局等关键参量的优选尚未很好解决［9］。

本文阐述了基于干扰失效角域以及干扰失效角域因子的新型评定方法，其中干扰失效角域为（对用户设备而言）无效干扰的来向集合，可直观显示空域滤波抗干扰方法的有效角度区域；干扰失效角域因子为干扰失效角域占整个空间立体角的百分比，可定量反映空域滤波抗干扰方法在整个空间的有效性。新型性能评定方法比基于零陷深度的性能评定方法全面、确切，可用于空域滤波的算法定量比较和关键参量优选，进而指导用户设备的抗干扰技术方案设计与实现。

2 相关知识

2.1 卫星导航用户设备

卫星导航系统由卫星系统、地面运行控制系统和应用系统三部分组成。应用系统中的用户设备是体现卫星导航系统功能性能的终端设备，其工作体制有卫星无线电测定业务 （RDSS）和卫星无线电导航业务 （RNSS）两种［7-8］。

RDSS为有源工作体制，用户设备需响应地面测量与控制中心 （MCC）发播、卫星转发的询问信号，而后发送定位、报文通信和定时等服务申请信号；MCC接收服务申请信号后，根据服务申请内容作相应处理；再经由卫星转发，使用户设备获得所申请的定位、报文通信和定时服务。RDSS体制以MCC的复杂性换取空间段卫星数量最少和卫星复杂度最低，仅由2颗卫星承担导航系统的数据交换和用户信息交换。

RNSS为无源工作体制，用户设备需接收4颗或4颗以上卫星发播的导航信号，获得卫星星历、伪距观测量、载波观测量等，进而解算出用户设备自身的位置、速度和时间 （PVT）［7］。

卫星的轨道高度约20 000km，有效全向辐射功率 （EIRP）仅30W左右。经过20 000km的扩散损耗后，到达用户设备的卫星信号功率比热噪声还低30dB左右。用户设备必须从如此弱的卫星信号中获取所需信息，因而具有电磁敏感度高的特点。电磁敏感度高具有两面性，一面是接收灵敏度高，另一面是抗电磁干扰能力弱。为此，常采用时域滤波、频域滤波和空域滤波等抗干扰技术提高抗电磁干扰能力，以满足复杂电磁环境下的应用需求［1-7，9］。

2.2 空域滤波抗干扰技术

与时域滤波、频域滤波相比，基于阵列天线的空域滤波具有对干扰类型、干扰带宽、非理想误差不敏感等优点，成为卫星导航用户设备的主流抗干扰技术［1-4］。

空域滤波根据卫星信号与干扰在功率、空间来向上的差异，基于阵列天线的加权矢量波束形成对干扰进行抑制。具体而言：首先利用阵列天线获得入射平面电磁波在各阵元上的感应信号（其波程差含入射波来向信息）；然后按照合理的优化准则及约束条件获得阵列天线加权矢量，使阵列天线方向图形成期望接收特性，即在干扰来向形成增益很低的零陷，在有用信号来向形成增益较高的波束；而后用阵列天线加权矢量对各阵元感应信号的幅度、时延进行补偿；最后将各补偿信号相加，实现抑制干扰、无失真接收卫星信号的目的。

对于K个卫星信号、J个干扰的情况，阵列天线上的感应信号矢量为

式 （1）中，r（t）＝ ［r1（t），…，rL（t）］T，a（sk）为第k个卫星信号的导向矢量，a（ij）为第j个干扰的导向矢量；n（t）＝ ［n1（t），…，nL（t）］T为热噪声矢量，nl（t）为第l（＝1，…，L）个阵元上的热噪声，包含背景噪声和通道噪声等；L为阵元数目。

空域滤波中常用的抗干扰算法有跟踪单星、跟踪多星和功率反演算法等［9］。

跟踪单星算法是附加了对单颗卫星接收增益约束的最小输出方差算法，即在无失真地接收指定一个卫星信号的前提下，使阵列天线的输出方差最小。跟踪单星算法的数学优化模型为

式 （2）中，w为阵列天线加权矢量，Rrr为阵列天线感应信号矢量的自相关矩阵，a（s1）为所指定卫星信号的导向矢量，记号H表示共轭转置。

跟踪多星算法是附加了对多颗卫星接收增益约束的最小输出方差算法，即在无失真地接收指定Q个卫星信号的前提下，使阵列天线的输出方差最小。跟踪多星算法的数学优化模型为

式 （3） 中，约 束 矩 阵 M ＝ ［a（s1），…，a（sQ）］，a（sq）为所指定第q（＝1，…，Q）个卫星信号的导向矢量；增益矢量1为Q维全1矢量，特别的Q取1时就为跟踪单星算法。

跟踪单星算法和跟踪多星算法需已知指定卫星信号的导向矢量，进而需已知卫星位置、阵列天线位置及姿态等信息。对于无法获得这些信息的场合，可采用功率反演算法，其数学优化模型如下

式 （4）中，约束矩阵退化为

L

维矢量δ

1

＝ ［1，0，…，0］

T

。

2.3 基于零陷深度的评定方法

空域滤波通过控制阵列天线方向图的方向特性，区别对待干扰、卫星信号；在干扰来向上的增益很低，以抑制干扰；在卫星信号来向上的增益高，以保留卫星信号。

基于零陷深度的评定方法依据空域滤波这一特点评定其抗干扰性能［1，4，7］，具体步骤如下：

（1）取定一个干扰来向 （仰角、方位角）；

（2）根据阵列天线构型、通道特性、抗干扰算法和非理想误差源等，计算该来向干扰时的阵列天线加权矢量；

（3）根据阵列天线加权矢量，计算阵列天线在空间各来向上的增益，获知阵列天线方向图特性；

（4）取阵列天线三维方向图在干扰来向上的增益，或者 （干扰仰角上）二维剖面图在干扰方位上的增益进行评定；

（5）若该增益比其他来向 （方位）上的增益低很多，表明空域滤波对干扰有响应。据此判定空域滤波起效；反之亦然。

显然，该方法只能给出空域滤波对该来向干扰有无响应以及响应强弱的结论；不能给出在其他来向干扰时的响应情况，以及干扰被抑制后用户设备的工作状态等；用其评定空域滤波的抗干扰性能难免偏颇。

举例说明：北斗用户设备采用基于5元均匀圆面阵、功率反演算法的空域滤波，所接收北斗东、西卫 星 信 号 来 向 分 别 为 ［304.18°，53.32°］和［222.05°，59.82°］。这里的5元均匀圆面阵是1个阵元在圆心、其余4个阵元均匀分布于半径为载波半波长的圆周上的阵列天线。

取定一个干扰来向 ［132.05°，39.82°］；根据阵列天线构型和2.2节的功率反演算法，计算阵列天线加权矢量；根据阵列天线加权矢量，获知阵列天线方向图；取图1所示 （干扰仰角39.82°上）二维剖面图在干扰方位角132.05°处的增益进行评定。由于图1所示二维剖面图在干扰方位角132.05°处的增益很低，基于零陷深度的评定方法据此判定空域滤波起效。

实际上，由图1只能获悉空域滤波对该来向干扰有一定程度地抑制。至于抑制程度是否满足（用户设备）后续信号信息处理的要求，以及在其他来向干扰情况下的抑制程度是否满足后续要求等均不得而知。

基于零陷深度的性能评定方法在全面性、确切性方面有缺陷的原因在于：度量零陷深度不具备在全空间来向上的统计性质，也不直接反映用户设备工作正常与否。

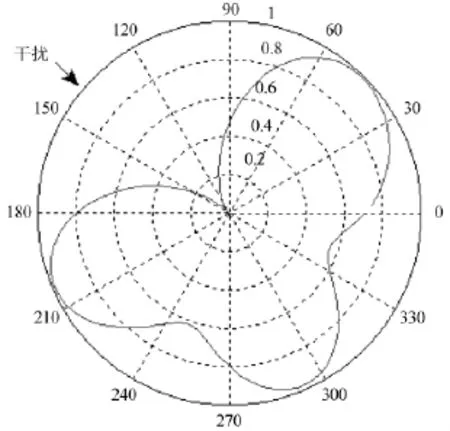
图1 阵列天线立体方向图在干扰仰角39.82°上的二维剖面图

3 新型评定方法

合理的抗干扰性能度量应能反映：在空间任意来向干扰情况下，采用空域滤波的用户设备正常工作的概率。依据这种具有全空间来向上统计性质、直接反映用户设备工作状态的度量，才能对空域滤波的抗干扰性能进行全面、确切地评定。

新型评定方法通过构造合理的抗干扰性能度量，继而进行客观、公正的性能评定。

3.1 干扰失效角域因子

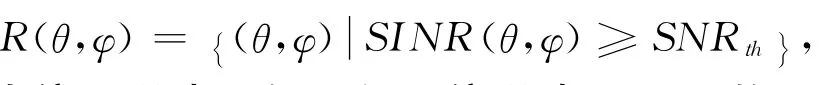
3.2 评定流程及步骤

新型评定方法的具体步骤如下：

（1）取定一个干扰来向 （仰角θ、方位角φ）；

（2）根据阵列天线构型、通道特性、抗干扰算法和非理想误差源等，计算该来向干扰时的阵列天线加权矢量w（θ，φ）；

（3）根据加权矢量w（θ，φ），统计对视野里第k（k＝1，…，K）个卫星信号的输出信干噪比SINRk（θ，φ）如下［9］

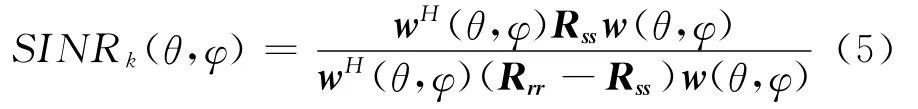
其中Rss＝Pska（sk）aH（sk）为第k个卫星信号矢量的自相关矩阵，Psk为第k个卫星信号的接收功率；

（4）重复步骤 （1）～步骤 （3），直至干扰仰角θ遍历 ［0，90°］、方位角φ遍历 ［0，360°）；

（5）确定正常接收视野里第k（k＝1，…，K）个卫星信号的干扰失效角域Rk（θ，φ）如下

（6）确定正常接收M个卫星信号的干扰失效角域R（θ，φ）

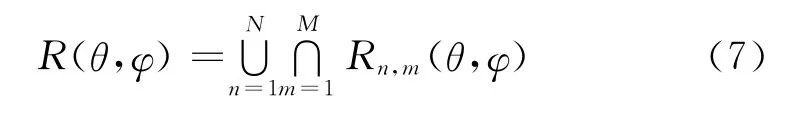
式 （7）中，Rn，m（θ，φ）为集合 ｛Rn，m（θ，φ）的第m个 元素，集合 ｛Rn，m（θ，φ是集合 ｛ ｛Rn，m（θ，φ）的第n个元素，｛｛Rn，m（θ，φ是由集合 ｛Rk（θ，φ构造出的嵌套子集合，即从｛Rk（θ，φ的K个元素中任选M个组成一个子集合，这样的子集合共N＝个。

特别的，对于RDSS工作体制，正常接收1个卫星信号即可，则M＝1。对于视野里只有1颗RDSS载荷卫星的情况有K＝1，则N＝1，进而

对于视野里有2颗RDSS载荷卫星的情况有K＝2，则N＝2，进而

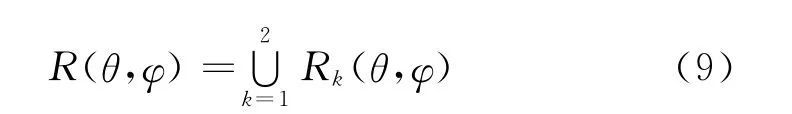
对于RNSS工作体制，需接收至少4个卫星信号才能实现PVT解算，则M＝4，进而干扰失效角域可具体化为

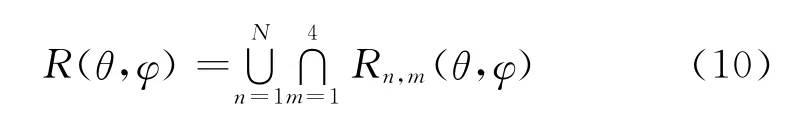
其中N＝

（7）计算干扰失效角域因子

新型评定方法的步骤 （3）～步骤 （7）与基于零陷深度的性能评定方法完全不同。

4 评定用例

下面采用新型评定方法对两种抗干扰算法的性能进行定量比较，在两种阵列天线布局之间进行优选。

两种待比较算法为跟踪单星算法和功率反演算法；两种待优选的阵列天线布局为5元均匀圆面阵和5元均匀圆环阵 （5个阵元均匀分布于半径为载波半波长的圆周上）。卫星信号来向与2.3节相同，门限信噪比为－20dB。

4.1 两种算法的定量比较

下面采用新型性能评定方法，对基于5元均匀园面阵的跟踪单星算法和功率反演算法的抗干扰性能进行定量比较。

首先，由2.2节中跟踪单星算法、功率反演算法的数学模型，可得相应的阵列天线加权矢量分别为

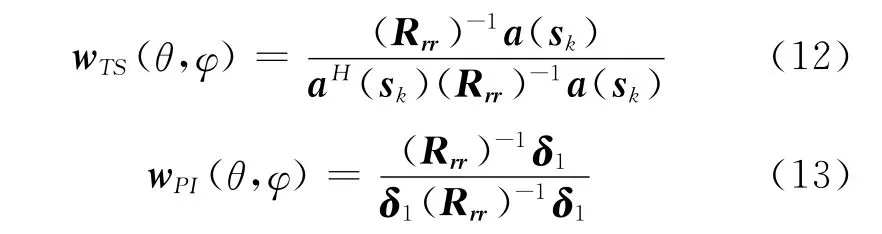
然后，可得跟踪单星算法对视野里第k个卫星信号的输出信干噪比为

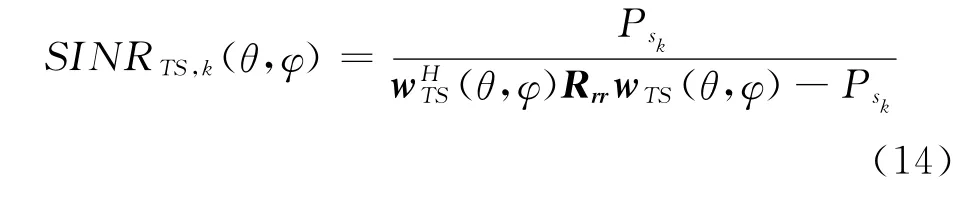
以及功率反演算法对视野里第k个卫星信号的输出信干噪比为

最后，与门限信噪比－20dB对比可得，图2、图3所示跟踪单星算法正常接收东、西卫星信号的角域；图4、图5所示功率反演算法正常接收东、西卫星信号的角域。来向属于图2、图4（图3、图5）所示区域的干扰，将不会影响用户设备对东（西）卫星信号的接收处理；反之亦然。

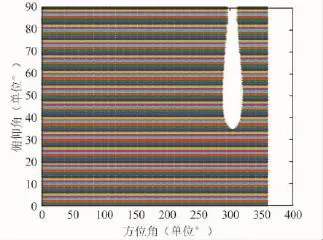
图2 跟踪单星算法正常接收东星信号的干扰失效角域

图3 跟踪单星算法正常接收西星信号的干扰失效角域

图4 功率反演算法正常接收东星信号的干扰失效角域

因视野里有2颗卫星，根据式 （9）干扰失效角域为正常接收东、西卫星信号角域的并集，进而得到图6所示跟踪单星算法的干扰失效角域，图7所示功率反演算法的干扰失效角域。

图5 功率反演算法正常接收西星信号的干扰失效角域

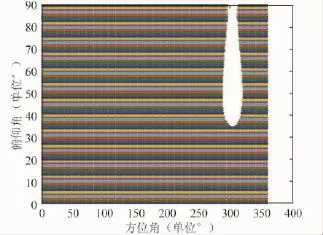
图6 跟踪单星算法的干扰失效角域

图7 功率反演算法的干扰失效角域 （五元均匀圆面阵）

再根据式 （11）可得：跟踪单星算法、功率反演算法对应的干扰失效角域因子分别为94.09%和59.81%，前者的抗干扰性能明显优于后者。

新型评定方法比基于零陷深度的评定方法更全面、确切，可定量比较两种算法的抗干扰性能。

4.2 两种阵列布局的优选

下面采用新型性能评定方法，从基于功率反演算法的5元均匀圆面阵和5元均匀圆环阵两种布局中加以优选。

图8 功率反演算法的干扰失效角域 （五元均匀圆环阵）

根据基于干扰失效角域因子的性能评定方法步骤，可得图8所示基于功率反演算法、5元均匀圆环阵的干扰失效角域，以及相应的干扰失效角域因子64.65%。与4.1节中基于功率反演算法、5元均匀圆面阵的干扰失效角域因子59.81%相比，5元均匀圆环阵的阵列天线布局较有优势。

5 结束语

新型性能评定方法所用度量干扰失效角域因子，能定量表征空间任意来向干扰情况下空域滤波方法有效的概率，比度量天线方向图的零陷深度全面、确切。新型性能评定方法可客观、公正地评定空域滤波方法的抗干扰性能，很好地解决了滤波算法的定量比较、关键参量的优选等问题。

［1］ZOLTOWSKI M D，GECAN A S.Advanced Adaptive Null Steering Concepts for GPS［C］//Military Communications Conference.California：IEEE Press，1995.1214－1218.

［2］FANTE R L，VACCARO J J.Wideband Cancellation of Interference in a GPS Receive Array［J］.IEEE Transactions on Aerospace and Electronic System，2000，36（2）：549－564.

［3］FANTE R L，VACCARO J J.Ensuring GPS Avaiability in an Interference Environment［C］//Position Location and Navigation Symposium.San Diego：IEEE Press，2000：37－40.

［4］BADKE B P.Global Positioning System Anti－jamming Techniques［D］.Arizona：Arizona State University，2002.

［5］聂俊伟，葛 锐，李垣陵，等.基于导航定位服务性能的GNSS天线阵抗干扰统计性能评估方法［J］.国防科技大学学报，2012，34（2）：81－87.

［6］KAPLAN E D，HEGARTY C J.Understanding GPS：Principles and Applications［M］.2nd Ed.Boston：Artech House，2006.

［7］李 跃，邱致和.导航与定位—信息化战争的北斗星［M］.2版.北京：国防工业出版社，2008.

［8］谭述森.广义RDSS全球定位报告系统［M］.北京：国防工业出版社，2011.

［9］李 琳，周文辉，谭述森.北斗用户机抗干扰低暴露技术研究［C］//中国卫星导航学术年会组委会.第一届中国卫星导航学术年会文集.北京：中国全球定位系统技术应用协会，2010：78－86.