离散数学中图论教学的探讨

吕诚，孙秀华

（安徽建筑大学数理系，安徽合肥230022）

离散数学中图论教学的探讨

吕诚，孙秀华

（安徽建筑大学数理系，安徽合肥230022）

离散数学图论部分具有概念多，定理多，内容丰富，学习难度大等特点，但其对计算机科学等相关专业大学生的后续课程又极为重要，因此本文试图探索如何激发贯穿整个课程的各种兴趣点，引导学生自发式学习.同时也探讨类比式的教学方式在该课程的具体实施方法.

离散数学；图论；欧拉图；哈密尔顿图；教学

1 引言

近年来,离散数学在现代科学中的重要性日益增加,已不仅是计算机专业的必备理论基础,也为其它工科专业和工程技术人员所必需.正鉴于此,各大高校的计算机专业、电子信息专业和计算信息专业等均开设《离散数学》课程[1,2]，并将其视为重要的专业基础课.图论作为《离散数学》课程的一个重要部分,在近几十年里得到迅速发展,并且图论的各种理论被大量应用于解决生产管理、军事、交通运输、计算机和通讯网络中的许多离散性问题，因而更加重要.于是有相当数量的高校还为高年级学生及研究生专门开设《图论》课程[3].图论部分的内容很多，解决问题的方式各不相同，特别是大量全新的概念和灵活多样的定理证明，且没有任何前期课程作为参考，对初学者有相当的难度，教学中也有着一定的困难.对于如何提高图论部分的教学，众多学者一直在做各种努力[4,5].本文将讨论兴趣教学和类比教学在该课程实施的方法,从而对教学工作者和广大学生起到一定的帮助.

2 兴趣带动教学的方式

提到以兴趣带动教学，众多授课教师都会在介绍图论这一章之前提及欧拉和“哥尼斯堡七桥问题”，这些内容可以极大地激发初学者的兴趣，并带动他们主动思考相关问题，从而带着问题进入本章内容.然而数学的学习通常都极为辛苦，单单上述兴趣不足以持续太久，学生的三分钟热度一过，又会觉得课程枯燥、烦闷，教学效果自然大打折扣.因而，本文主张将兴趣教学贯穿始终，从培养学生对图论这一全新内容的兴趣，到将已有的兴趣激发并转化为强烈的学习欲望，更好地完成本课程的教学.

其实可以激发学生兴趣的方法很多，在各个内容中都可找到兴趣点，让学生觉得每个知识点都颇有意思.比如通过介绍数学史，如上述“哥尼斯堡七桥问题”，也可以是该课程的一些重大问题，特别是前人的智慧都无法解决的，对于提升学习该课程的动力更为明显.当介绍到汉密尔顿图时，可指出将一个图的每一顶点均视为某个城市，每条边视为某两个城市间的道路，哈密尔顿图则可以理解为遍历所有城市且不重复经过任意城市，即通常所说的“环游世界问题”，而且这一问题至今没能给出有效地方法完全解决，只能得到某些充分条件和某些必要条件，亦可适当引导学生思考这些为什么不能统一起来得到充要条件.当介绍到图的同构概念时，也可说明这也是图论学科需要解决的一个重要问题，即如何有效地判断图的同构.当介绍到平面图及图的染色时，可介绍著名的“四色猜想”：在1852年英国一名青年盖思里发现在给英国地图染色时只需四种颜色即可，且四种颜色是必要的，于是提出猜想：任何地图上的国家只须四种颜色来染，使得任何具有共同边界的两个国家颜色都不相同.1878年伦敦数学会负责人凯莱向伦敦数学会成员正式宣布了这一问题，并形成当时著名的“四色猜想”.在随后一百多年里，很多人“证明”了这一结论，却又被发现这些都是失败的证明.最终1976年美国伊利诺斯大学的阿佩尔和海肯两名教授借助计算机花费1200多个小时，讨论了近两千个可约构形后，宣布“四色猜想”成为“四色定理”.然而计算机的证明却并没有给予人们信服，因为检验这近两千个可约构形绝非易事，因而寻求“通常”的方法——即非机器的数学证明来解决这一问题，仍然十分重要，这一点至今没有做到.这就是我们所试图达到的：介绍本课程现存的重要问题，令学生在无从寻找参考答案的情况下进行思考，感受课程的魅力，提高学习兴趣.

有时介绍某些复杂的定义时，难免会然学生感觉生硬，单从定义也很难让学生理解.于是如果能够用其解决某些实际问题，可加深学生对概念的理解与运用.比如刚开始介绍图论正文，便有一堆概念和定义，单是图的定义就有好几百字，讲解完毕后，学生却一头雾水，仍没弄清顶点、边等概念.这时可以令学生思考如下问题：在某个集会时，恰有6人坐在同一桌上，则或者其中有三人两两相识，或者三人两两都不相识.在给出的数分钟里，学生们无法给出解决的思路，我们却可以告诉他们用图的定义可以轻松解答.我们记x1、x2、x3、x4、x5、x6六个顶点表示六个人，并用不同颜色的边来表示两人之间的关系，如果两人相互认识，就用黄线连接，如果两人不认识，就用黑线连接.现在只需证明这个图中必含有一个同色的三角形.不妨取点x1，则与x1相连的边中至少有三条同色，设x1x2、x1x3和x1x4为黄边.现考查三角形x2x3x4，若其中有一条黄边，设x2x3，则x1x2x3为黄边三角形；若没有一条为黄边，则x2x3x4本身为黑边三角形.这一简单应用同样可以带来意想不到的教学效果.

3 类比教学的方式

图论中涉及众多概念，而且很多概念有相关之处，不易区分.在指导学生学习时不妨采用类比的方式加以强化.比如欧拉图与哈密尔顿图，欧拉图是数学家欧拉为解决著名的“哥尼斯堡七桥问题”而得出的，并由此产生了图论这门新兴学科；哈密尔顿图由“环游世界游戏”而得出，至今仍未能给出哈密尔顿图存在的充分必要条件.这两种图作为图论中的重点和难点对于初学者有相当大的难度.我可通过举例将他们进行类比，加以区分.

例[2](a)画一个图使它既是欧拉图又是哈密尔顿图.

(b)画一个图使它是欧拉图但不是哈密尔顿图.

(c)画一个图使它是哈密尔顿图但不是欧拉图.

(d)画一个图使它既不是欧拉图又不是哈密尔顿图.

初学者看到此类练习,很少能有清晰的思路,众多辅导书或习题解答常给出较为繁琐的图例[6],不太容易构造也不利学生理解,有的学生甚至还需花上一些时间来判断为什么这种图符合条件.我们在此给出简易的结论，并辅以适当简洁的图例,找出其中的规律，同时可加深对欧拉回路与哈密尔顿回路的区分.

定理1[2]图G具有一条欧拉路径当且仅当G具有零个或两个奇数次数的顶点.

定理2[2]一个连通图是欧拉图当且仅当该图的顶点次数都是偶数.

定理3[2]若图G=是哈密尔顿图,则对V的每个非空真子集S均成立:ω(G-S)≤|S|,其中|S|表示S中的顶点数,ω(G-S)表示G删去顶点集S后得到的图的连通分图个数.

结论4由定义知判断一个图是否为欧拉图,就是判断该图能否一笔画出,即所谓的“一笔画问题”.根据上述定理1、定理2可知判断一个图是否为欧拉图,只需数一下该图每个顶点的边数是否都是偶数.

结论5由定理3可知判断一个图是不是哈密尔顿图,可采用删除结点的方法.

解(a')我们画一个三角形或一个四边形，因它们显然可以一笔画出且经过所有的点，故既是欧拉图又是哈密尔顿图.图例如下：

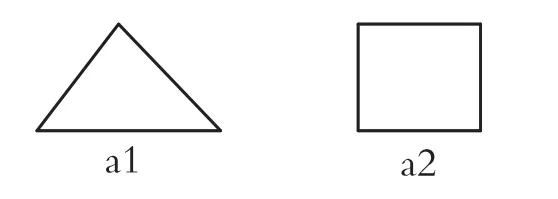
(b')由于所需的图不是哈密尔顿图,可考虑将两个图通过合并某一结点粘合为一个图,这样删除该结点便得到两个分图,于是不满足定理3，从而不是哈密尔顿图.又要求是欧拉图,故用来粘合的图可选择具有欧拉回路的图,这样粘合后所得图的每个顶点的次数仍为偶数,故仍为欧拉图.于是我们将两个三角形或一个三角形与一个四边形通过一个结点而粘合.图例如下：

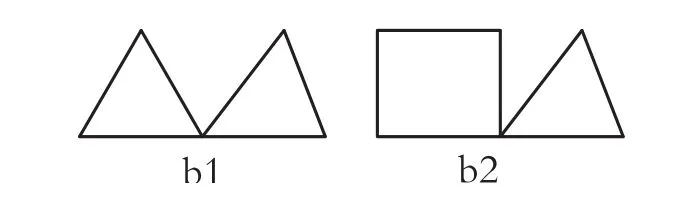
(c')由于所需的图是哈密尔顿图而不是欧拉图,故只需找一四边形,通过加上一些边使其具有奇数次数的顶点,从而不是欧拉图.图例如下:

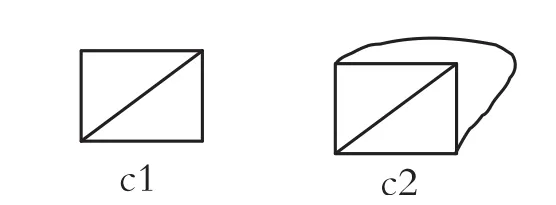
(d')由于所需图既不是欧拉图又不是哈密尔顿图，故可选用“图(c1)”，再用(b')粘合的方法将其转化为非哈密尔顿图.或选用“图(b2)”由(c')中添加边的方法将其转化为非欧拉图.图例如下：

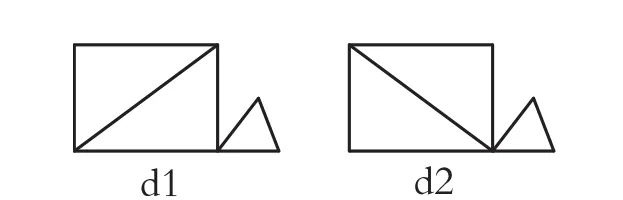
〔1〕屈婉玲,耿素云,张立昂.离散数学[M].北京:清华大学出版社,2005.

〔2〕方世昌.离散数学[M].西安:西安电子科技大学出版社, 1996.

〔3〕徐俊明.图论及其应用[M].合肥:中国科学技术大学出版社,1998.

〔4〕翟明清.浅析图论教学[J].大学数学,2011，27(5):203-206.

〔5〕田京京.信息专业图论课教学改革和实践[J].中国电力教育，2011(8)：114-116.

〔6〕孙学红，秦伟良.离散数学习题解答[M].西安:西安电子科技大学出版社,1999.

〔7〕左孝凌.离散数学理论、分析、题解[M].上海:上海科学技术出版社,1988.

G642

A

1673-260X（2013）07-0219-02

安徽省自然基金项目资助(KJ2011z057)